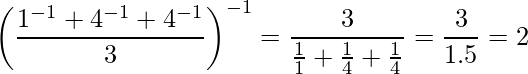armonic_mean() en Python

La media armónica (también conocida como media contraria) es uno de varios tipos de media y, en particular, una de las medias pitagóricas. Por lo general, se usa en situaciones en las que se desean tasas promedio. La media armónica es también el recíproco de la media aritmética de los recíprocos de un conjunto dado de observaciones.

Por ejemplo, la media armónica de 1, 4 y 4 se puede calcular como: 

La media armónica se puede incorporar en Python3 usando la función harmonic_mean() del módulo de estadísticas.  

Sintaxis: harmonic_mean ([conjunto de datos])
Parámetros:  
[conjunto de datos] : que es una lista o tupla o iterador de números con valores reales.
Returntype: Devuelve el armonic_mean del conjunto de datos dado.
Errores y excepciones:
StatisticsError cuando se pasa un conjunto de datos vacío o si el conjunto de datos consta de valores negativos. 
TypeError para conjuntos de datos de valores de tipo no numérico. 
 

Nota: La media armónica se calcula solo usando valores positivos en la lista, el conjunto o cualquier secuencia. 
 
Código #1: 

# Python3 code to demonstrate the
# working of harmonic_mean() function
 
# Import statistics module
import statistics
 
# list of positive real valued numbers
data = [1, 3, 5, 7, 9]
 
# using harmonic mean function to calculate
# the harmonic mean of the given data-set
print("Harmonic Mean is % s " % (statistics.harmonic_mean(data)))

Producción : 

Harmonic Mean is 2.797513321492007 

Código #2: 

# Python3 program to demonstrate harmonic_mean()
# function from the statistics module
 
# Importing the statistics module
from statistics import harmonic_mean
 
# Importing fractions module as fr
from fractions import Fraction as fr
 
# tuple of positive integer numbers
data1 = (2, 3, 4, 5, 7, 9, 11)
 
# tuple of a set of floating-point values
data2 = (2.4, 5.1, 6.7, 8.9)
 
# tuple of a set of fractional numbers
data3 = (fr(1, 2), fr(44, 12), fr(10, 3), fr(2, 3))
 
# dictionary of a set of values
# Only the keys are taken in
# consideration by harmonic_mean()
data4 = {1: "one", 2: "two", 3: "three"}
 
# Printing the harmonic mean of above datasets
print("Harmonic Mean of data set 1 is % s"
                 % (harmonic_mean(data1)))
                  
print("Harmonic Mean of data set 2 is % s"
                 % (harmonic_mean(data2)))
 
print("Harmonic Mean of data set 3 is % s"
                 % (harmonic_mean(data3)))
                  
print("Harmonic Mean of data set 4 is % s"
                % (harmonic_mean(data4)))

Producción : 

Harmonic Mean of data set 1 is 4.299197943900386
Harmonic Mean of data set 2 is 4.574783168721765
Harmonic Mean of data set 4 is 55/56
Harmonic Mean of data set 5 is 1.6363636363636365

Código #3: Demostración de error de estadísticas 

# Python code to demonstrate StatisticsError
# while using harmonic_mean()
 
# importing statistics module
import statistics
 
# data-set of numbers containing
# a negative number
dat1 = [1, -1]
 
# Statistics Error is raised when the
# data-set passed as parameter is
# empty or contain a negative value
print(statistics.harmonic_mean(dat1))

Producción : 

Traceback (most recent call last):
  File "C:/Users/Souveek/PycharmProjects/Test.py", line 12, in 
    print(statistics.harmonic_mean((1, -1)))
  File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 356, in harmonic_mean
    T, total, count = _sum(1/x for x in _fail_neg(data, errmsg))
  File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 148, in _sum
    for n, d in map(_exact_ratio, values):
  File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 356, in 
    T, total, count = _sum(1/x for x in _fail_neg(data, errmsg))
  File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 285, in _fail_neg
    raise StatisticsError(errmsg)
statistics.StatisticsError: harmonic mean does not support negative values

Nota: Es posible que los siguientes códigos no se ejecuten en IDE en línea, ya que la función harmonic_mean() se introdujo recientemente en Python3.6 
  
Aplicaciones: 
Harmonic Mean es una de las muchas herramientas importantes en finanzas (en estadísticas). La media armónica ponderada es el método preferible para promediar múltiplos, como la relación precio-beneficio (P/E), en la que el precio está en el numerador. También se usa en cálculos en lugares donde la media aritmética sobreestima el resultado requerido.