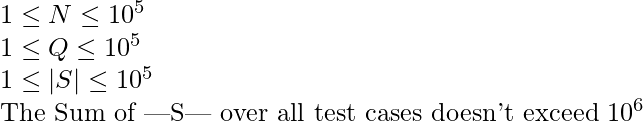Función hash
Una función Hash es una función que asigna cualquier tipo de datos de tamaño arbitrario a valores de tamaño fijo. Los valores devueltos por la función se denominan valores hash o resúmenes. Hay muchas funciones hash populares como DJBX33A, MD5 y SHA-256. Esta publicación discutirá las características clave, la implementación, las ventajas y los inconvenientes de la función Polynomial Rolling Hash.
Tenga en cuenta que si dos strings son iguales, sus valores hash también deberían ser iguales. Pero lo contrario no tiene por qué ser cierto.
La función hash rodante polinomial
La función hash rodante polinomial es una función hash que usa solo multiplicaciones y sumas. La siguiente es la función:
![]()
o simplemente,
![Rendered by QuickLaTeX.com \text{hash(s)} = \displaystyle\sum_{i = 0}^{n - 1} s[i]\cdot p^i\quad \text{mod}\ m](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54b5d229f345f66c8f94a6f059c01019_l3.png)
Dónde
- La entrada a la función es una string
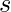 de longitud
de longitud 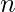 .
. 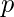 y
y 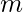 son algunos enteros positivos.
son algunos enteros positivos.- La elección de
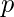 y
y 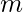 afecta el rendimiento y la seguridad de la función hash.
afecta el rendimiento y la seguridad de la función hash. - Si la string
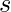 consta solo de letras minúsculas, entonces
consta solo de letras minúsculas, entonces  es una buena opción.
es una buena opción.
- Los programadores competitivos prefieren usar un valor mayor para
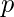 . Los ejemplos incluyen
. Los ejemplos incluyen 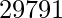 ,
,  ,
,  .
.
- Los programadores competitivos prefieren usar un valor mayor para
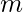 será necesariamente un primo grande ya que la probabilidad de que dos claves colisionen (produzcan el mismo hash) es casi
será necesariamente un primo grande ya que la probabilidad de que dos claves colisionen (produzcan el mismo hash) es casi  .
.  y
y 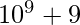 son valores ampliamente utilizados para
son valores ampliamente utilizados para 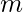 .
.- La salida de la función es el valor hash de la string
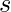 que oscila entre
que oscila entre 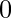 e
e 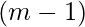 inclusive.
inclusive.
A continuación se muestra la implementación de la función Polynomial Rolling Hash
C
#include <stdio.h>
#include <string.h>
int get_hash(const char* s, const int n) {
const int p = 31, m = 1e9 + 7;
int hash = 0;
long p_pow = 1;
for(int i = 0; i < n; i++) {
hash = (hash + (s[i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash;
}
int main() {
char s[] = "geeksforgeeks";
int n = strlen(s);
printf("Hash of %s is %d\n", s, get_hash(s, n));
return 0;
}
C++
#include <bits/stdc++.h>
using namespace std;
struct Hash {
const int p = 31, m = 1e9 + 7;
int hash_value;
Hash(const string& s) {
int hash_so_far = 0;
long p_pow = 1;
const int n = s.length();
for (int i = 0; i < n; ++i) {
hash_so_far = (hash_so_far + (s[i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
hash_value = hash_so_far;
}
bool operator==(const Hash& other) {
return (hash_value == other.hash_value);
}
};
int main() {
const string s = "geeksforgeeks";
Hash h(s);
cout << "Hash of " << s << " is: " << h.hash_value << '\n';
return 0;
}
Java
class Hash {
final int p = 31, m = 1000000007;
int hash_value;
Hash(String S) {
int hash_so_far = 0;
final char[] s = S.toCharArray();
long p_pow = 1;
final int n = s.length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far + (s[i] - 'a' + 1) * p_pow) % m);
p_pow = (p_pow * p) % m;
}
hash_value = hash_so_far;
}
}
class Main {
public static void main(String[] args) {
String s = "geeksforgeeks";
Hash h = new Hash(s);
System.out.println("Hash of " + s + " is " + h.hash_value);
}
}
Python3
class Hash:
def __init__(self, s: str):
self.hash_value = 0
self.p, self.m = 31, 10**9 + 7
self.length = len(s)
hash_so_far = 0
p_pow = 1
for i in range(self.length):
hash_so_far = (hash_so_far + (1 + ord(s[i]) - ord('a')) * p_pow) % self.m
p_pow = (p_pow * self.p) % self.m
self.hash_value = hash_so_far
def __eq__(self, other):
return self.hash_value == other.hash_value
if __name__ == '__main__':
s = "geeksforgeeks"
h = Hash(s)
print("Hash value of {} is {}".format(s, h.hash_value))
Hash of geeksforgeeks is 609871790
Colisiones en polinomio Rolling Hash
Dado que la salida de la función Hash es un número entero en el rango ![]() , hay muchas posibilidades de que dos strings produzcan el mismo valor hash.
, hay muchas posibilidades de que dos strings produzcan el mismo valor hash.
Por ejemplo, las strings ![]() y
y ![]() producen el mismo valor hash para
producen el mismo valor hash para ![]() y
y ![]() .
.
Además, las strings ![]() y
y ![]() producen el mismo valor hash para
producen el mismo valor hash para ![]() y
y ![]() .
.
Podemos garantizar una colisión dentro de un dominio muy pequeño. Considere un conjunto de strings, ![]() , que consta solo de letras minúsculas, de modo que la longitud de cualquier string
, que consta solo de letras minúsculas, de modo que la longitud de cualquier string ![]() no exceda
no exceda ![]() .
.
tenemos ![]() _ Dado que el rango de la función Hash es
_ Dado que el rango de la función Hash es ![]() , el mapeo uno a uno es imposible. Por lo tanto, podemos garantizar una colisión generando arbitrariamente dos strings cuya longitud no exceda
, el mapeo uno a uno es imposible. Por lo tanto, podemos garantizar una colisión generando arbitrariamente dos strings cuya longitud no exceda ![]() .
.
Resolución de colisión
Podemos notar que el valor de ![]() afecta las posibilidades de colisión. Hemos visto que la probabilidad de colisión es
afecta las posibilidades de colisión. Hemos visto que la probabilidad de colisión es ![]() . Podemos aumentar el valor de
. Podemos aumentar el valor de ![]() para reducir la probabilidad de colisión. Pero eso afecta la velocidad del algoritmo. Cuanto mayor sea el valor de
para reducir la probabilidad de colisión. Pero eso afecta la velocidad del algoritmo. Cuanto mayor sea el valor de ![]() , más lento será el algoritmo. Además, algunos lenguajes (C, C++, Java) tienen un límite en el tamaño del número entero. Por lo tanto, no podemos aumentar el valor de
, más lento será el algoritmo. Además, algunos lenguajes (C, C++, Java) tienen un límite en el tamaño del número entero. Por lo tanto, no podemos aumentar el valor de ![]() a un valor muy grande.
a un valor muy grande.
Entonces, ¿cómo podemos minimizar las posibilidades de una colisión?
Tenga en cuenta que el hash de una string depende de dos parámetros: ![]() y
y ![]() .
.
Hemos visto que las strings ![]() y
y ![]() producen el mismo valor hash para
producen el mismo valor hash para ![]() y
y ![]() . Pero para
. Pero para ![]() y
y ![]() , producen hashes diferentes.
, producen hashes diferentes.
Observación:
Si dos strings producen los mismos valores hash para un par
, producirán valores hash diferentes para un par diferente,
.
Estrategia:
Sin embargo, no podemos anular las posibilidades de colisión porque hay infinitas strings. Pero, seguramente, podemos reducir la probabilidad de que dos cuerdas choquen.
Podemos reducir la probabilidad de colisión generando un par de hashes para una string determinada. El primer hash se genera usando ![]() y
y ![]() , mientras que el segundo hash se genera usando
, mientras que el segundo hash se genera usando ![]() y
y ![]() .
.
¿Por qué funcionará esto?
Estamos generando dos hashes utilizando dos valores de módulo diferentes, ![]() y
y ![]() . La probabilidad de una colisión es ahora
. La probabilidad de una colisión es ahora 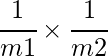 . Dado que ambos
. Dado que ambos ![]() y
y ![]() son mayores que
son mayores que ![]() , la probabilidad de que ocurra una colisión ahora es menor, lo
, la probabilidad de que ocurra una colisión ahora es menor, lo ![]() que es mucho mejor que la probabilidad original de colisión,
que es mucho mejor que la probabilidad original de colisión, ![]() .
.
A continuación se muestra la implementación para el mismo
C
#include <stdio.h>
#include <string.h>
int get_hash1(const char* s, int length) {
const int p = 31, m = 1e9 + 7;
int hash_value = 0;
long p_pow = 1;
for(int i = 0; i < length; i++) {
hash_value = (hash_value + (s[i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash_value;
}
int get_hash2(const char* s, int length) {
const int p = 37, m = 1e9 + 9;
int hash_value = 0;
long p_pow = 1;
for(int i = 0; i < length; i++) {
hash_value = (hash_value + (s[i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash_value;
}
int main() {
char s[] = "geeksforgeeks";
int length = strlen(s);
int hash1 = get_hash1(s, length);
int hash2 = get_hash2(s, length);
printf("Hash values of %s are: (%d, %d)\n", s, hash1, hash2);
return 0;
}
C++
#include <bits/stdc++.h>
using namespace std;
struct Hash {
const int p1 = 31, m1 = 1e9 + 7;
const int p2 = 37, m2 = 1e9 + 9;
int hash1 = 0, hash2 = 0;
Hash(const string& s) {
compute_hash1(s);
compute_hash2(s);
}
void compute_hash1(const string& s) {
long p_pow = 1;
for(char ch: s) {
hash1 = (hash1 + (ch + 1 - 'a') * p_pow) % m1;
p_pow = (p_pow * p1) % m1;
}
}
void compute_hash2(const string& s) {
long p_pow = 1;
for(char ch: s) {
hash2 = (hash2 + (ch + 1 - 'a') * p_pow) % m2;
p_pow = (p_pow * p2) % m2;
}
}
// For two strings to be equal
// they must have same hash1 and hash2
bool operator==(const Hash& other) {
return (hash1 == other.hash1 && hash2 == other.hash2);
}
};
int main() {
const string s = "geeksforgeeks";
Hash h(s);
cout << "Hash values of " << s << " are: ";
cout << "(" << h.hash1 << ", " << h.hash2 << ")" << '\n';
return 0;
}
Java
class Hash {
final int p1 = 31, m1 = 1000000007;
final int p2 = 37, m2 = 1000000009;
int hash_value1, hash_value2;
Hash(String s) {
compute_hash1(s);
compute_hash2(s);
}
void compute_hash1(String s) {
int hash_so_far = 0;
final char[] s_array = s.toCharArray();
long p_pow = 1;
final int n = s_array.length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far + (s_array[i] - 'a' + 1) * p_pow) % m1);
p_pow = (p_pow * p1) % m1;
}
hash_value1 = hash_so_far;
}
void compute_hash2(String s) {
int hash_so_far = 0;
final char[] s_array = s.toCharArray();
long p_pow = 1;
final int n = s_array.length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far + (s_array[i] - 'a' + 1) * p_pow) % m2);
p_pow = (p_pow * p2) % m2;
}
hash_value2 = hash_so_far;
}
}
class Main {
public static void main(String[] args) {
String s = "geeksforgeeks";
Hash h = new Hash(s);
System.out.println("Hash values of " + s + " are: " + h.hash_value1 + ", " + h.hash_value2);
}
}
Python3
class Hash:
def __init__(self, s: str):
self.p1, self.m1 = 31, 10**9 + 7
self.p2, self.m2 = 37, 10**9 + 9
self.hash1, self.hash2 = 0, 0
self.compute_hashes(s)
def compute_hashes(self, s: str):
pow1, pow2 = 1, 1
hash1, hash2 = 0, 0
for ch in s:
seed = 1 + ord(ch) - ord('a')
hash1 = (hash1 + seed * pow1) % self.m1
hash2 = (hash2 + seed * pow2) % self.m2
pow1 = (pow1 * self.p1) % self.m1
pow2 = (pow2 * self.p2) % self.m2
self.hash1, self.hash2 = hash1, hash2
def __eq__(self, other):
return self.hash1 == other.hash1 and self.hash2 == other.hash2
def __str__(self):
return f'({self.hash1}, {self.hash2})'
if __name__ == '__main__':
s = "geeksforgeeks"
hash = Hash(s)
print("Hash of " + s + " is " + str(hash))
Hash values of geeksforgeeks are: (609871790, 642799661)
Características de la función hash rodante polinomial
Cálculo de hashes de cualquier substring de una string dada en 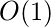
Tenga en cuenta que calcular el hash de la string S también calculará los hash de todos los prefijos. Solo tenemos que almacenar los valores hash de los prefijos mientras computamos. Digamos que \text{hash[i]} denota el hash del prefijo \text{S[0…i]}, tenemos
![]()
Esto nos permite calcular rápidamente el hash de la substring ![]() siempre
siempre ![]() que tengamos poderes de
que tengamos poderes de ![]() preparación.
preparación.
El comportamiento del hash cuando se cambia un carácter.
Recuerde que el hash de una string ![]() viene dado por
viene dado por
![Rendered by QuickLaTeX.com \text{hash(s)} = \displaystyle\sum_{i = 0}^{n - 1} s[i]\cdot p^i\quad \text{mod}\ m](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54b5d229f345f66c8f94a6f059c01019_l3.png)
Digamos que cambiamos un carácter ![]() en algún índice
en algún índice ![]() a algún otro carácter
a algún otro carácter ![]() . ¿Cómo cambiará el hash?
. ¿Cómo cambiará el hash?
Si ![]() denota el valor hash antes de cambiar y
denota el valor hash antes de cambiar y ![]() es el valor hash después de cambiar, entonces la relación entre ellos viene dada por
es el valor hash después de cambiar, entonces la relación entre ellos viene dada por
![]()
Por lo tanto, las consultas se pueden realizar muy rápidamente en lugar de volver a calcular el hash desde el principio, siempre que tengamos los poderes de ![]() listo.
listo.
A continuación se proporciona una implementación más elegante.
C++
#include <bits/stdc++.h>
using namespace std;
long long power(long long x, long long y, long long p) {
long long result = 1;
for(; y; y >>= 1, x = x * x % p) {
if(y & 1) {
result = result * x % p;
}
}
return result;
}
long long inverse(long long x, long long p) {
return power(x, p - 2, p);
}
class Hash {
private:
int length;
const int mod1 = 1e9 + 7, mod2 = 1e9 + 9;
const int p1 = 31, p2 = 37;
vector<int> hash1, hash2;
pair<int, int> hash_pair;
public:
inline static vector<int> inv_pow1, inv_pow2;
inline static int inv_size = 1;
Hash() {}
Hash(const string& s) {
length = s.size();
hash1.resize(length);
hash2.resize(length);
int h1 = 0, h2 = 0;
long long p_pow1 = 1, p_pow2 = 1;
for(int i = 0; i < length; i++) {
h1 = (h1 + (s[i] - 'a' + 1) * p_pow1) % mod1;
h2 = (h2 + (s[i] - 'a' + 1) * p_pow2) % mod2;
p_pow1 = (p_pow1 * p1) % mod1;
p_pow2 = (p_pow2 * p2) % mod2;
hash1[i] = h1;
hash2[i] = h2;
}
hash_pair = make_pair(h1, h2);
if(inv_size < length) {
for(; inv_size < length; inv_size <<= 1);
inv_pow1.resize(inv_size, -1);
inv_pow2.resize(inv_size, -1);
inv_pow1[inv_size - 1] = inverse(power(p1, inv_size - 1, mod1), mod1);
inv_pow2[inv_size - 1] = inverse(power(p2, inv_size - 1, mod2), mod2);
for(int i = inv_size - 2; i >= 0 && inv_pow1[i] == -1; i--) {
inv_pow1[i] = (1LL * inv_pow1[i + 1] * p1) % mod1;
inv_pow2[i] = (1LL * inv_pow2[i + 1] * p2) % mod2;
}
}
}
int size() {
return length;
}
pair<int, int> prefix(const int index) {
return {hash1[index], hash2[index]};
}
pair<int, int> substr(const int l, const int r) {
if(l == 0) {
return {hash1[r], hash2[r]};
}
int temp1 = hash1[r] - hash1[l - 1];
int temp2 = hash2[r] - hash2[l - 1];
temp1 += (temp1 < 0 ? mod1 : 0);
temp2 += (temp2 < 0 ? mod2 : 0);
temp1 = (temp1 * 1LL * inv_pow1[l]) % mod1;
temp2 = (temp2 * 1LL * inv_pow2[l]) % mod2;
return {temp1, temp2};
}
bool operator==(const Hash& other) {
return (hash_pair == other.hash_pair);
}
};
int main() {
string my_str = "geeksforgeeks";
const int n = my_str.length();
auto hash = Hash(my_str);
auto hash_pair = hash.substr(0, n - 1);
cout << "Hashes of the string " << my_str << " are:\n";
cout << hash_pair.first << ' ' << hash_pair.second << '\n';
return 0;
}
En la implementación anterior, estamos calculando las inversas de las potencias de $p$en tiempo lineal.
Aplicaciones:
Considere este problema: Dada una secuencia S de N strings y Q consultas. En cada consulta, se le dan dos índices, i y j, su tarea es encontrar la longitud del prefijo común más largo de las strings S[i] y S[j].
Antes de entrar en el enfoque para resolver este problema, tenga en cuenta que las restricciones son:
Usando Hashing, el problema se puede resolver en O(N + Q/log|S|_{max}). El enfoque es calcular hashes para todas las strings en tiempo O (N). Luego, para cada consulta, podemos buscar binariamente la longitud del prefijo común más largo usando hashing. La implementación de este enfoque se proporciona a continuación.
C++14
#include <bits/stdc++.h>
using namespace std;
long long power(long long x, long long y, long long p) {
long long result = 1;
for(; y; y >>= 1, x = x * x % p) {
if(y & 1) {
result = result * x % p;
}
}
return result;
}
long long inverse(long long x, long long p) {
return power(x, p - 2, p);
}
class Hash {
private:
int length;
const int mod1 = 1e9 + 7, mod2 = 1e9 + 9;
const int p1 = 31, p2 = 37;
vector<int> hash1, hash2;
pair<int, int> hash_pair;
public:
inline static vector<int> inv_pow1, inv_pow2;
inline static int inv_size = 1;
Hash() {}
Hash(const string& s) {
length = s.size();
hash1.resize(length);
hash2.resize(length);
int h1 = 0, h2 = 0;
long long p_pow1 = 1, p_pow2 = 1;
for(int i = 0; i < length; i++) {
h1 = (h1 + (s[i] - 'a' + 1) * p_pow1) % mod1;
h2 = (h2 + (s[i] - 'a' + 1) * p_pow2) % mod2;
p_pow1 = (p_pow1 * p1) % mod1;
p_pow2 = (p_pow2 * p2) % mod2;
hash1[i] = h1;
hash2[i] = h2;
}
hash_pair = make_pair(h1, h2);
if(inv_size < length) {
for(; inv_size < length; inv_size <<= 1);
inv_pow1.resize(inv_size, -1);
inv_pow2.resize(inv_size, -1);
inv_pow1[inv_size - 1] = inverse(power(p1, inv_size - 1, mod1), mod1);
inv_pow2[inv_size - 1] = inverse(power(p2, inv_size - 1, mod2), mod2);
for(int i = inv_size - 2; i >= 0 && inv_pow1[i] == -1; i--) {
inv_pow1[i] = (1LL * inv_pow1[i + 1] * p1) % mod1;
inv_pow2[i] = (1LL * inv_pow2[i + 1] * p2) % mod2;
}
}
}
int size() {
return length;
}
pair<int, int> prefix(const int index) {
return {hash1[index], hash2[index]};
}
pair<int, int> substr(const int l, const int r) {
if(l == 0) {
return {hash1[r], hash2[r]};
}
int temp1 = hash1[r] - hash1[l - 1];
int temp2 = hash2[r] - hash2[l - 1];
temp1 += (temp1 < 0 ? mod1 : 0);
temp2 += (temp2 < 0 ? mod2 : 0);
temp1 = (temp1 * 1LL * inv_pow1[l]) % mod1;
temp2 = (temp2 * 1LL * inv_pow2[l]) % mod2;
return {temp1, temp2};
}
bool operator==(const Hash& other) {
return (hash_pair == other.hash_pair);
}
};
void query(vector<Hash>& hashes, const int N) {
int i = 0, j = 0;
cin >> i >> j;
i--, j--;
int lb = 0, ub = min(hashes[i].size(), hashes[j].size());
int max_length = 0;
while(lb <= ub) {
int mid = (lb + ub) >> 1;
if(hashes[i].prefix(mid) == hashes[j].prefix(mid)) {
if(mid + 1 > max_length) {
max_length = mid + 1;
}
lb = mid + 1;
}
else {
ub = mid - 1;
}
}
cout << max_length << '\n';
}
int main() {
int N = 0, Q = 0;
cin >> N >> Q;
vector<Hash> hashes;
for(int i = 0; i < N; i++) {
string s;
cin >> s;
hashes.push_back(Hash(s));
}
for(; Q > 0; Q--) {
query(hashes, N);
}
return 0;
}
Input: 5 4 geeksforgeeks geeks hell geeksforpeaks hello 1 2 1 3 3 5 1 4Expected Output: 5 0 4 8