Sean a y b cualquier número entero y g su máximo común divisor de a y b . Entonces, existen enteros x e y tales que ax por
![]()
![]()
Podemos encontrar x’ e y’ que satisfagan (1) utilizando algoritmos euclidianos . Todas las soluciones posibles de (1) están dadas por,
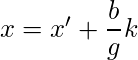
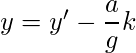
![]()
donde k es cualquier número entero.
Es fácil ver por qué esto se sostiene. Simplemente conecte las soluciones a (1) para tener una intuición.
Además, es importante ver que para la ecuación general de la forma,
![]()
u=gcd(a, b) es el entero positivo más pequeño para el cual ax+by=u tiene una solución con valores integrales de x e y .
Declaración: Si mcd(a, c)=1 y mcd(b, c)=1, entonces mcd(ab, c)=1.
Prueba:
Lo anterior se puede probar fácilmente usando la Identidad de Bezout.
ax+cy=1 y bu+cv=1
Multiplica las dos ecuaciones anteriores,
(ax+cy)(bu+cv)=1
Lo anterior implica,
1 es el único número entero que divide LHS y RHS.
Por lo tanto, mcd(ab, c) = 1.
Referencia:
https://brilliant.org/wiki/bezouts-identity/
https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity
Publicación traducida automáticamente
Artículo escrito por arvinderavy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA