DFA o Deterministic Finite Automata es una máquina de estados finitos, en la que en cada alfabeto de entrada se realiza una transición de un estado a otro de acuerdo con un conjunto de reglas definidas según la necesidad de aceptación de strings.
En este problema particular, las series de longitud son el factor a tener en cuenta. Los alfabetos de entrada son {a, b}. Ninguna tirada de longitud inferior a 4 significa que cualquier alfabeto de entrada se repite un mínimo de 4 veces.
Ejemplo:
Entrada: n = “aaabab”
Salida: string no aceptada
Explicación: La letra inicial a no se repite al menos 4 veces. Por lo tanto, DFA falló.Entrada: n = “aaaabbbbaaaabbbbbaaaaa”
Salida: string aceptada
Explicación: Cada aparición única de a y b se repite al menos 4 veces. Por lo tanto, DFA pasó.
Diseño de DFA paso a paso:
Paso 1: Primero tenemos que pensar en qué alfabeto de entrada se ingresa. Como se trata de un mínimo de 4 carreras de longitud. Tome el alfabeto de entrada es ‘a’ en el estado «A» y marque este estado como estado inicial. La siguiente transición ocurre en la entrada ‘a’:
- Del estado “A” al estado “B”
- Del estado “B” al estado “C”
- Del estado “C” al estado “D”
- Del estado “D” al estado “E”
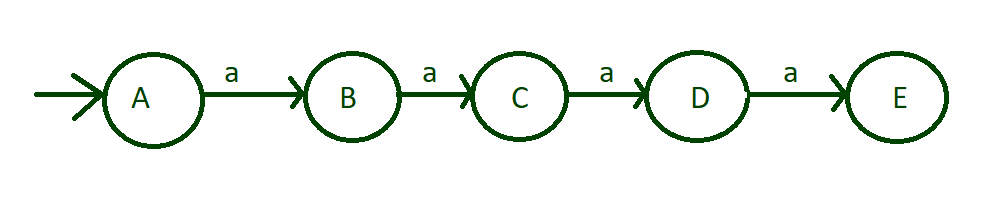
entrada de corrida de longitud 4
Paso 2: Al igual que en el paso anterior, se ingresan un mínimo de 4 a, lo cual es aceptable, por lo que el estado «E» es el estado final. También se aceptan corridas de longitud superior a 4, así que coloque el bucle automático de ‘a’ en el estado final «E».
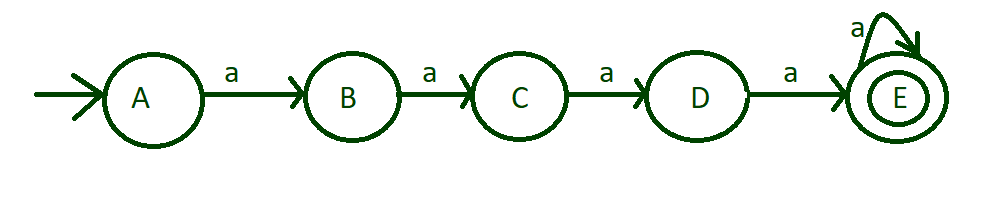
marca el estado «E» al estado final
Paso 3: Hasta ahora, el diseño de la máquina se realiza con el alfabeto de entrada ‘a’. Pero el alfabeto de entrada ‘b’ del estado «A» se deja para tratar. Ahora haga el mismo proceso con el alfabeto de entrada ‘b’ en el estado «A». La siguiente transición ocurre en la entrada ‘b’:
- Del estado “A” al estado “F”
- Del estado “F” al estado “G”
- Del estado “G” al estado “H”
- Del estado “H” al estado “Q”
Marque el estado «Q» hasta el estado final. Y también se aceptan ejecuciones de más de 4 de longitud, así que coloque el bucle automático en el estado final «Q».
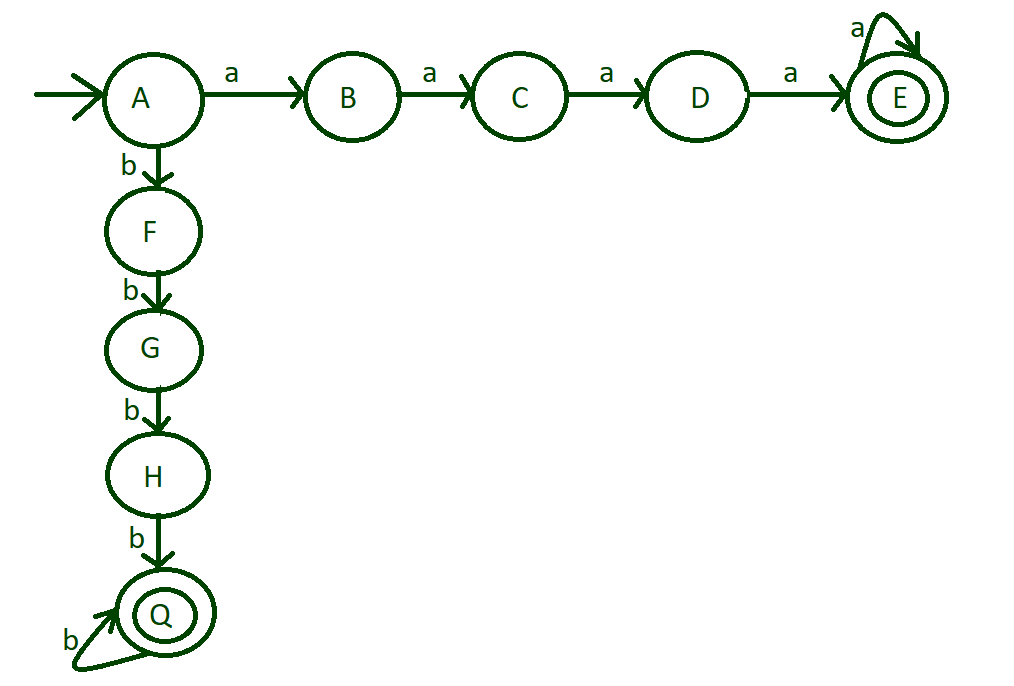
transiciones del alfabeto de entrada ‘b’
Paso 4: Hasta ahora lo hemos hecho con una sola entrada a o b, es decir, aaaa y bbbb, pero ahora nos ocupamos de ambas entradas, como aaaabbbb o aaaabbbbaaaaa, etc.
Para esta transición de la entrada ‘b’ desde el estado «E» al estado “F” y transición de la entrada ‘a’ del estado “Q” al estado “B”.

Paso 5: ahora se trata de los alfabetos de entrada restantes, hasta ahora la máquina diseñada ha cubierto todos los casos aceptables posibles y ninguno de los alfabetos de entrada restantes pasará al estado muerto «DS».
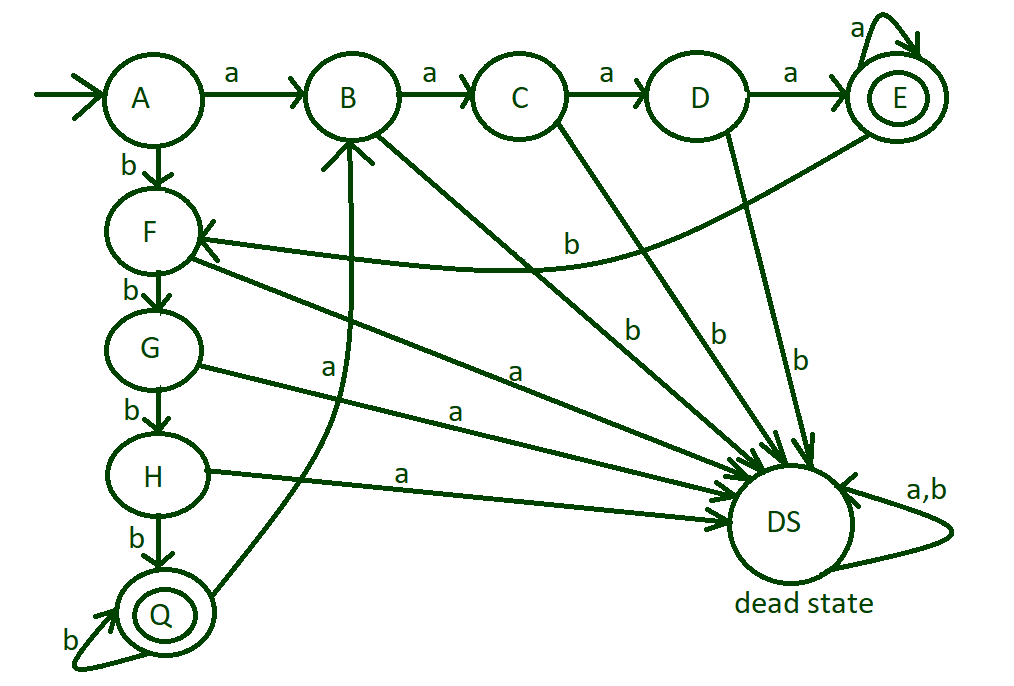
diseño final
Tabla de transición de DFA anterior:
aquí «A» es el estado inicial y «E» y «Q» son estados finales. DS se denomina ESTADO MUERTO
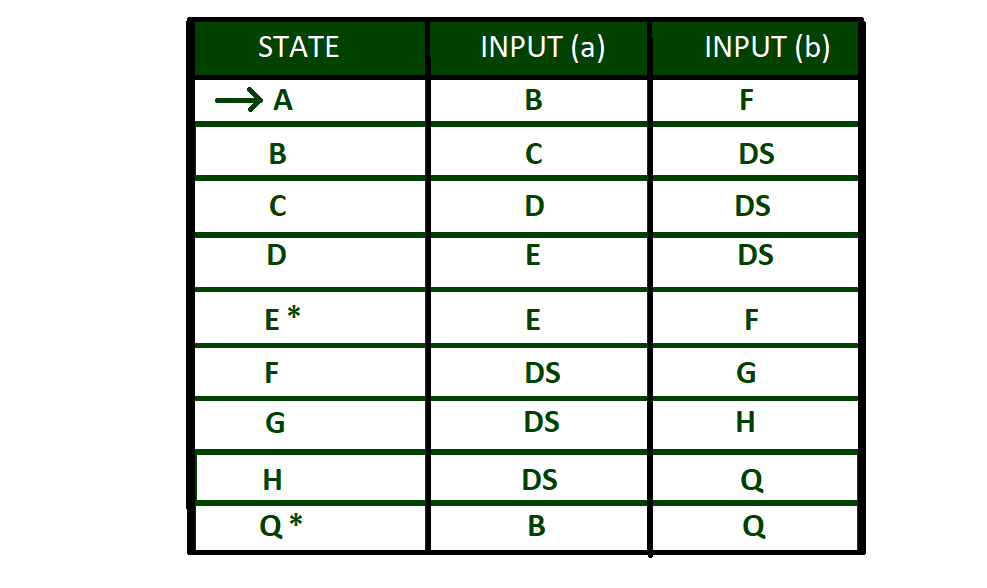
Tabla de transición
Implementación de Python de DFA anterior:
Python3
def checkStateA(n):
# if length of is 0
# print string not accepted
if(len(n)== 0):
print("string not accepted")
else:
# if 'a' is found
# call stateB function
# else call stateF
# function
if(n[0]=='a'):
stateB(n[1:])
else:
stateF(n[1:])
def stateB(n):
# if length of is 0
# print string not accepted
if (len(n)== 0):
print("string not accepted")
else:
# if 'a' is found
# call stateC function
# print string not
# accepted
if(n[0]=='a'):
stateC(n[1:])
else:
print("string not accepted")
def stateC(n):
# if length of is 0
# print string not accepted
if (len(n)== 0):
print("string not accepted")
else:
# if 'a' is found
# call stateD function
# print string not
# accepted
if(n[0]=='a'):
stateD(n[1:])
else:
print("string not accepted")
def stateD(n):
# if length of is 0
# print string not accepted
if(len(n)== 0):
print("string not accepted")
else:
# if 'a' is found
# call stateE function
# print string not
# accepted
if(n[0]=='a'):
stateE(n[1:])
else:
print("string not accepted")
def stateE(n):
# if length of is 0
# print string accepted
if(len(n)== 0):
print("string accepted")
# if 'a' is found
# call stateE function
# if 'b' is found
# call stateF function
elif(n[0]=='a'):
stateE(n[1:])
elif(n[0]=='b'):
stateF(n[1:])
def stateF(n):
# if length of is 0
# print string not accepted
if(len(n)== 0):
print("string not accepted")
else:
# if 'b' is found
# call stateG function
# print string not
# accepted
if(n[0]=='b'):
stateG(n[1:])
else:
print("string not accepted")
def stateG(n):
# if length of is 0
# print string not accepted
if(len(n)== 0):
print("string not accepted")
else:
# if 'b' is found
# call stateHfunction
# print string not
# accepted
if(n[0]=='b'):
stateH(n[1:])
else:
print("string not accepted")
def stateH(n):
# if length of is 0
# print string not accepted
if(len(n)== 0):
print("string not accepted")
else:
# if 'b' is found
# call stateQ function
# print string not
# accepted
if(n[0]=='b'):
stateQ(n[1:])
else:
print("string not accepted")
def stateQ(n):
# if length of is 0
# print string accepted
if(len(n)== 0):
print("string accepted")
else:
# if 'b' is found
# call stateQ function
# else call stateB function
if(n[0]=='b'):
stateQ(n[1:])
elif(n[0]=='a'):
stateB(n[1:])
# Driver code
if __name__ == '__main__':
# input string 1
n ="aaaabbbbbaaaa"
# function call to check the string
checkStateA(n)
# input string 2
n ="aaaabbb"
# function call to check the string
checkStateA(n)
string accepted string not accepteed
Publicación traducida automáticamente
Artículo escrito por _mridul_bhardwaj_ y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA