Implementación de Series de Fourier hasta ‘n’ Armónicos en MATLAB

En cálculo matemático, la forma expandida de una función periódica “f(x)” en términos de una suma infinita de cosenos y senos se denomina serie de Fourier. Hace uso de las relaciones de ortogonalidad de las funciones coseno y seno. En otras palabras, la serie de Fourier también se puede definir como una forma de representar cualquier función periódica “f(x)” como una suma de funciones coseno y seno (posiblemente infinitas). 

Para una función periódica “f(x)”, la serie de Fourier de “f(x)” en el Rango de [ c, c+2 l ] viene dada por:

 (En general, l =π)  

Aquí:

Aquí, a _n & b _n se denominan coeficientes de seno y coseno de Fourier, respectivamente.  

Nota: Si en la fórmula anterior de la Serie de Fourier, en lugar de Infinito, usamos la suma de n=1 a n=k, entonces la llamamos serie de Fourier de f(x) hasta armónicos ‘k’.

Las funciones de MATLAB utilizadas en el código son:

• disp(“txt”): este método muestra el mensaje-“txt” al usuario.
• entrada («txt»): este método muestra el mensaje-«txt» y espera a que el usuario ingrese un valor y presione la tecla Retorno.
• int(y,x ₁ ,x ₂ ): este método calcula la integral definida de ‘y’ de x ₁ a x ₂ .
• vpa(f,4): este método evalúa cada elemento de ‘f’ en al menos 4 dígitos significativos.
• ezplot(y,[x ₁ ,x ₂ ]): este método traza ‘y’ en el intervalo especificado [x ₁ ,x ₂ ].
• title(‘GFG’): Este método agrega el título-“GFG” especificado a una gráfica.
• legend(A,B,…): este método crea una leyenda con etiquetas descriptivas para cada línea trazada.
• strcat(A,B): este método concatena horizontalmente el texto en sus argumentos de entrada. 
• char(f): este método convierte la array de entrada ‘f’ en una array de caracteres.

Ejemplo:

% MATLAB code for Implementation of
% Fourier Series up to 'n' Harmonics in MATLAB:
clear all
clc      
disp("Implementation of Fourier Series
up to 'n' Harmonics in MATLAB | GeeksforGeeks")
syms x
 
f=input("Enter the function of x, whose fourier series is to be found:");
I=input("Enter the limits of Integration [a , b] :");
k=input("Enter the number of Harmonics:");
 
% Lower limit of Integration
a=I(1); 
 
 % Upper limit of Integration
b=I(2);
l=(b-a)/2;
a0=(1/l)*(int(f,a,b));
Fx=a0/2;
 
% Calculating the nth Harmonic
for n=1:k   
%To creates a new figure window
% using default property values
    figure; 
    an(n)=(1/l)*(int(f*cos(n*pi*x/l),a,b));
    bn(n)=(1/l)*(int(f*sin(n*pi*x/l),a,b));
    Fx=Fx+((an(n))*cos(n*pi*x/l))+((bn(n))*sin(n*pi*x/l));
     
    % To evaluate Each element of
     % Fx to at least 4-Significant digits
    Fx=vpa(Fx,4);       
     
    % To plot the curve Fx (Fourier series upto
    % nth Harmonic) in the given interval [a,b]
    ezplot(Fx,[a,b]);  
     
    % To add a second line plot (Given Function/f) without deleting
    % the existing line plot (Fourier series upto nth Harmonic/Fx)
    hold on;             
    ezplot(f,[a,b]);     
     
    % To plot the curve f (Given Function)
    % in the given interval [a,b]
    title(["The Fourier series upto ", num2str(n)," Harmonics is:"]);
     
    % To create a legend with descriptive labels
    % for both of the plotted lines (f & Fx)
    legend("Fourier series","Given Function"); 
    
   % To set the hold state to off
    hold off;            
end
disp(strcat('The Fourier series upto ', num2str(n),' Harmonics is:',char(Fx)))

Producción:

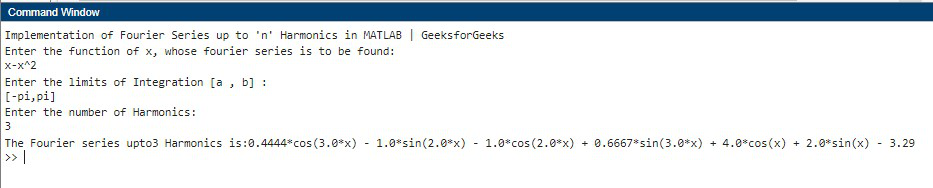
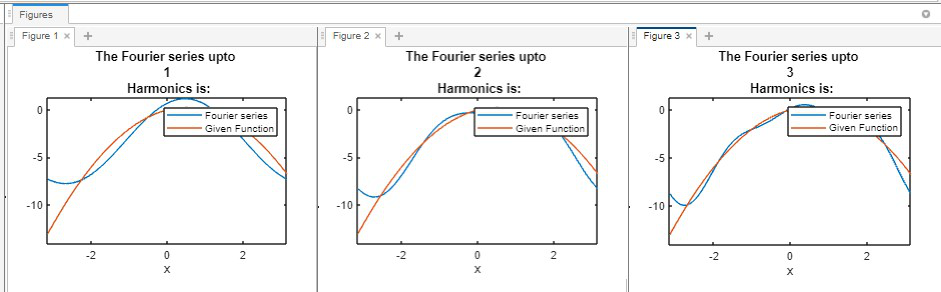
Input: For a function  in the Range= [ -π, π ],
       Fourier Series of f(x) up to '3' Harmonics is:

 

 

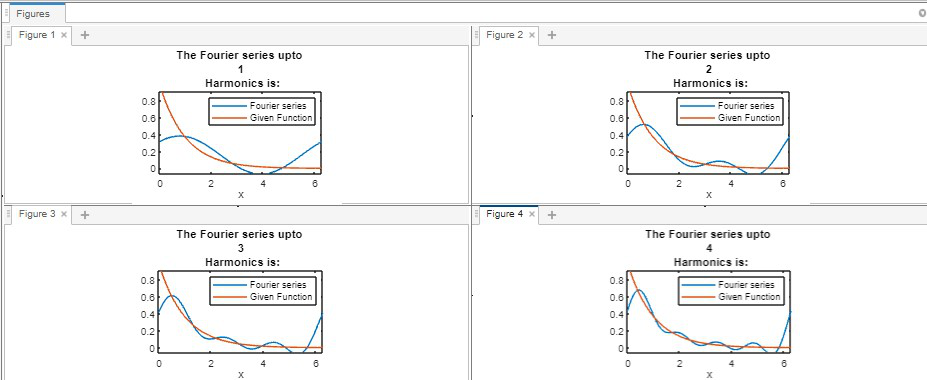
Input: For a function f(x)=e-x in the Range= [ 0, 2π ],
       Fourier Series of f(x) up to '4' Harmonics is: