Implementando el proceso de entrenamiento de Redes Neuronales Artificiales en Python

Una red neuronal artificial (ANN) es un paradigma de procesamiento de información que se inspira en el cerebro. Las RNA, como las personas, aprenden con el ejemplo. Una ANN se configura para una aplicación específica, como el reconocimiento de patrones o la clasificación de datos, a través de un proceso de aprendizaje. El aprendizaje implica en gran medida ajustes en las conexiones sinápticas que existen entre las neuronas. 
 
 

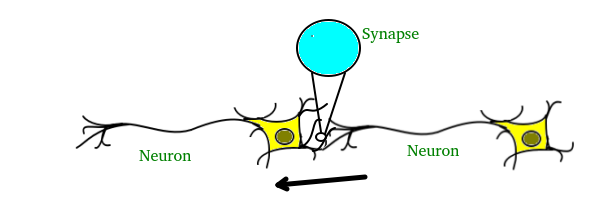
El cerebro consta de cientos de miles de millones de células llamadas neuronas. Estas neuronas están conectadas entre sí por sinapsis que no son más que las conexiones a través de las cuales una neurona puede enviar un impulso a otra neurona. Cuando una neurona envía una señal excitatoria a otra neurona, esta señal se sumará a todas las demás entradas de esa neurona. Si excede un umbral dado, hará que la neurona objetivo envíe una señal de acción hacia adelante: así es como funciona internamente el proceso de pensamiento.
En Ciencias de la Computación, modelamos este proceso creando «redes» en una computadora usando arrays. Estas redes pueden entenderse como una abstracción de neuronas sin tener en cuenta todas las complejidades biológicas. Para mantener las cosas simples, solo modelaremos un NN simple, con dos capas capaces de resolver un problema de clasificación lineal.
 

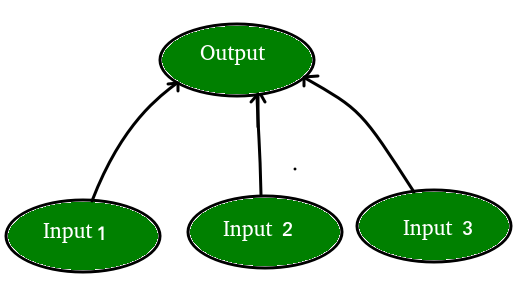
Digamos que tenemos un problema en el que queremos predecir la salida dado un conjunto de entradas y salidas como ejemplo de entrenamiento así:

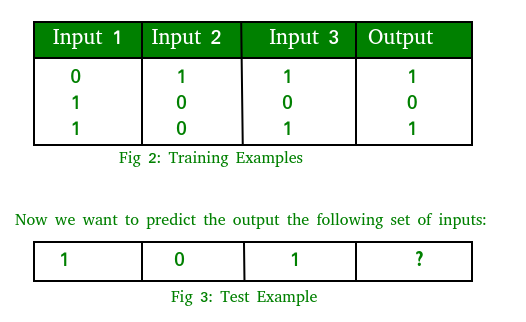
Tenga en cuenta que la salida está directamente relacionada con la tercera columna, es decir, los valores de la entrada 3 es lo que es la salida en cada ejemplo de entrenamiento en la fig. 2. Entonces, para el ejemplo de prueba, el valor de salida debe ser 1.
 

El proceso de formación consta de los siguientes pasos: 

1. Propagación directa: 
   tome las entradas, multiplique por los pesos (solo use números aleatorios como pesos) 
   Sea Y = W _i I _i  = W ₁ I ₁ +W ₂ I ₂ +W ₃ I ₃ 
   Pase el resultado a través de una fórmula sigmoidea para calcular la salida de la neurona. La función Sigmoid se usa para normalizar el resultado entre 0 y 1: 
   1/1 + e ^-y
2. Back Propagation 
   Calcula el error, es decir, la diferencia entre la salida real y la salida esperada. Dependiendo del error, ajuste los pesos multiplicando el error con la entrada y nuevamente con el gradiente de la curva sigmoidea: 
   Peso += Error Entrada Salida (1-Salida), aquí la Salida (1-Salida) es derivada de la curva sigmoidea.

Nota: Repita todo el proceso durante unas pocas miles de iteraciones.
Codifiquemos todo el proceso en Python. Usaremos la biblioteca Numpy para ayudarnos con todos los cálculos en arrays fácilmente. Necesitaría instalar una biblioteca numpy en su sistema para ejecutar el 
comando de código para instalar numpy: 

 sudo apt -get install python-numpy

Implementación:

from joblib.numpy_pickle_utils import xrange
from numpy import *
  
  
class NeuralNet(object):
    def __init__(self):
        # Generate random numbers
        random.seed(1)
  
        # Assign random weights to a 3 x 1 matrix,
        self.synaptic_weights = 2 * random.random((3, 1)) - 1
  
    # The Sigmoid function
    def __sigmoid(self, x):
        return 1 / (1 + exp(-x))
  
    # The derivative of the Sigmoid function.
    # This is the gradient of the Sigmoid curve.
    def __sigmoid_derivative(self, x):
        return x * (1 - x)
  
    # Train the neural network and adjust the weights each time.
    def train(self, inputs, outputs, training_iterations):
        for iteration in xrange(training_iterations):
            # Pass the training set through the network.
            output = self.learn(inputs)
  
            # Calculate the error
            error = outputs - output
  
            # Adjust the weights by a factor
            factor = dot(inputs.T, error * self.__sigmoid_derivative(output))
            self.synaptic_weights += factor
  
        # The neural network thinks.
  
    def learn(self, inputs):
        return self.__sigmoid(dot(inputs, self.synaptic_weights))
  
  
if __name__ == "__main__":
    # Initialize
    neural_network = NeuralNet()
  
    # The training set.
    inputs = array([[0, 1, 1], [1, 0, 0], [1, 0, 1]])
    outputs = array([[1, 0, 1]]).T
  
    # Train the neural network
    neural_network.train(inputs, outputs, 10000)
  
    # Test the neural network with a test example.
    print(neural_network.learn(array([1, 0, 1])))

Salida esperada: después de 10 iteraciones, nuestra red neuronal predice que el valor será 0,65980921. No parece bueno, ya que la respuesta debería ser 1. Si aumentamos el número de iteraciones a 100, obtenemos 0,87680541. ¡Nuestra red se está volviendo más inteligente! Posteriormente, para 10000 iteraciones obtenemos 0,9897704, que está bastante cerca y, de hecho, es un resultado satisfactorio.
Referencias: 
 

• REDES NEURONALES de Christos Stergiou y Dimitrios Siganos
• Fundamentos del aprendizaje profundo: comenzando con la red neuronal artificial
• Juega con una red neuronal aquí mismo en tu navegador
• Redes neuronales desmitificadas

Este artículo es una contribución de Vivek Pal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.