Imprima todas las permutaciones posibles de un Array/Vector sin duplicados usando Backtracking

Dados los números de vectores , la tarea es imprimir todas las permutaciones posibles del vector dado utilizando el retroceso  .

Ejemplos :

Entrada : nums[] = {1, 2, 3}
Salida : {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 2, 1}, {3, 1, 2}
Explicación : hay 6 permutaciones posibles

Entrada : nums[] = {1, 3}
Salida : {1, 3}, {3, 1}
Explicación : Hay 2 permutaciones posibles

Enfoque : La tarea se puede resolver con la ayuda de retroceder . Un artículo similar para una mejor comprensión está aquí: Imprimir todas las permutaciones de una string dada 

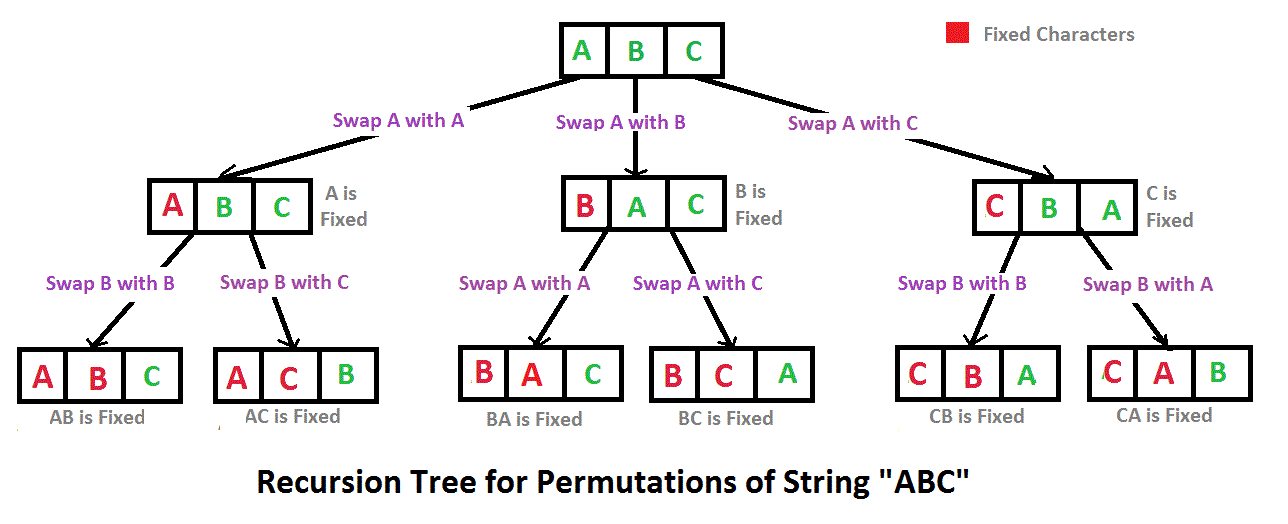
A continuación se muestra la implementación del código anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function for swapping two numbers
void swap(int& x, int& y)
{
    int temp = x;
    x = y;
    y = temp;
}
 
// Function to find the possible
// permutations
void permutations(vector<vector<int> >& res,
                  vector<int> nums, int l, int h)
{
    // Base case
    // Add the vector to result and return
    if (l == h) {
        res.push_back(nums);
        return;
    }
 
    // Permutations made
    for (int i = l; i <= h; i++) {
 
        // Swapping
        swap(nums[l], nums[i]);
 
        // Calling permutations for
        // next greater value of l
        permutations(res, nums, l + 1, h);
 
        // Backtracking
        swap(nums[l], nums[i]);
    }
}
 
// Function to get the permutations
vector<vector<int> > permute(vector<int>& nums)
{
    // Declaring result variable
    vector<vector<int> > res;
    int x = nums.size() - 1;
 
    // Calling permutations for the first
    // time by passing l
    // as 0 and h = nums.size()-1
    permutations(res, nums, 0, x);
    return res;
}
 
// Driver Code
int main()
{
    vector<int> nums = { 1, 2, 3 };
    vector<vector<int> > res = permute(nums);
 
    // printing result
    for (auto x : res) {
        for (auto y : x) {
            cout << y << " ";
        }
        cout << endl;
    }
 
    return 0;
}

// Java program for the above approach
 
import java.util.ArrayList;
import java.util.Arrays;
 
public class GFG
{
    // Function for swapping two numbers
    static void swap(int nums[], int l, int i)
    {
        int temp = nums[l];
        nums[l] = nums[i];
        nums[i] = temp;
    }
 
    // Function to find the possible
    // permutations
    static void permutations(ArrayList<int[]> res,
                             int[] nums, int l, int h)
    {
        // Base case
        // Add the array to result and return
        if (l == h) {
            res.add(Arrays.copyOf(nums, nums.length));
            return;
        }
 
        // Permutations made
        for (int i = l; i <= h; i++) {
            // Swapping
            swap(nums, l, i);
 
            // Calling permutations for
            // next greater value of l
            permutations(res, nums, l + 1, h);
 
            // Backtracking
            swap(nums, l, i);
        }
    }
 
    // Function to get the permutations
    static ArrayList<int[]> permute(int[] nums)
    {
        // Declaring result variable
        ArrayList<int[]> res = new ArrayList<int[]>();
        int x = nums.length - 1;
 
        // Calling permutations for the first
        // time by passing l
        // as 0 and h = nums.size()-1
        permutations(res, nums, 0, x);
        return res;
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int[] nums = { 1, 2, 3 };
        ArrayList<int[]> res = permute(nums);
 
        // printing result
        for (int[] x : res) {
            for (int y : x) {
                System.out.print(y + " ");
            }
            System.out.println();
        }
    }
}
 
// This code is contributed by jainlovely450

# Python program for the above approach
 
# Function to find the possible
# permutations
def permutations(res, nums, l, h) :
     
    # Base case
    # Add the vector to result and return
    if (l == h) :
        res.append(nums);
        for i in range(len(nums)):
            print(nums[i], end=' ');
 
        print('')
        return;
 
    # Permutations made
    for i in range(l, h + 1):
         
        # Swapping
        temp = nums[l];
        nums[l] = nums[i];
        nums[i] = temp;
 
        # Calling permutations for
        # next greater value of l
        permutations(res, nums, l + 1, h);
 
        # Backtracking
        temp = nums[l];
        nums[l] = nums[i];
        nums[i] = temp;
 
# Function to get the permutations
def permute(nums):
     
    # Declaring result variable
    x = len(nums) - 1;
    res = [];
     
    # Calling permutations for the first
    # time by passing l
    # as 0 and h = nums.size()-1
    permutations(res, nums, 0, x);
    return res;
 
# Driver Code
nums = [ 1, 2, 3 ];
res = permute(nums);
 
# This code is contributed by Saurabh Jaiswal

<script>
 
// JavaScript program for the above approach
 
// Function to find the possible
// permutations
function permutations(res, nums, l, h)
{
     
    // Base case
    // Add the vector to result and return
    if (l == h)
    {
        res.push(nums);
        for(let i = 0; i < nums.length; i++)
            document.write(nums[i] + ' ');
 
        document.write('<br>')
        return;
    }
 
    // Permutations made
    for(let i = l; i <= h; i++)
    {
         
        // Swapping
        let temp = nums[l];
        nums[l] = nums[i];
        nums[i] = temp;
 
        // Calling permutations for
        // next greater value of l
        permutations(res, nums, l + 1, h);
 
        // Backtracking
        temp = nums[l];
        nums[l] = nums[i];
        nums[i] = temp;
    }
}
 
// Function to get the permutations
function permute(nums)
{
     
    // Declaring result variable
    let x = nums.length - 1;
    let res = [];
     
    // Calling permutations for the first
    // time by passing l
    // as 0 and h = nums.size()-1
    permutations(res, nums, 0, x);
    return res;
}
 
// Driver Code
let nums = [ 1, 2, 3 ];
let res = permute(nums);
 
// This code is contributed by Potta Lokesh
 
</script>

1 2 3 
1 3 2 
2 1 3 
2 3 1 
3 2 1 
3 1 2 

Complejidad de tiempo : O(N*N!) Tenga en cuenta que hay N! permutaciones y requiere tiempo O(N) para imprimir una permutación.
Espacio Auxiliar : O(r – l)