Dado un gráfico no dirigido que consta de N Nodes en forma de array de adyacencia graph[][] de tamaño N*N , la tarea es imprimir todos los ciclos hamiltonianos posibles en el gráfico no dirigido dado (tomando el vértice inicial como ‘0’).
Un ciclo hamiltoniano (o circuito hamiltoniano) es un camino hamiltoniano tal que hay un borde (en el gráfico) desde el último vértice hasta el primer vértice del camino hamiltoniano.
Ejemplos:
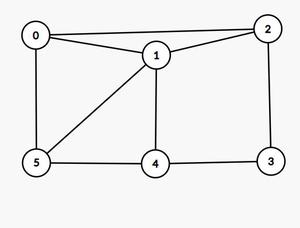
Entrada: gráfico[][] = {{0, 1, 1, 0, 0, 1}, {1, 0, 1, 0, 1, 1}, {1, 1, 0, 1, 0, 0} , {0, 0, 1, 0, 1, 0}, {0, 1, 0, 1, 0, 1}, {1, 1, 0, 0, 1, 0}}
Salida:
0 1 2 3 4 5 0
0 1 5 4 3 2 0
0 2 3 4 1 5 0
0 2 3 4 5 1 0
0 5 1 4 3 2 0
0 5 4 3 2 1 0
Explicación:
Todos los ciclos hamiltonianos posibles para el siguiente gráfico (con el vértice inicial como 0) son
- {0 → 1 → 2 → 3 → 4 → 5 → 0}
- {0 → 1 → 5 → 4 → 3 → 2 → 0}
- {0 → 2 → 3 → 4 → 1 → 5 → 0}
- {0 → 2 → 3 → 4 → 5 → 1 → 0}
- {0 → 5 → 1 → 4 → 3 → 2 → 0}
- {0 → 5 → 4 → 3 → 2 → 1 → 0}
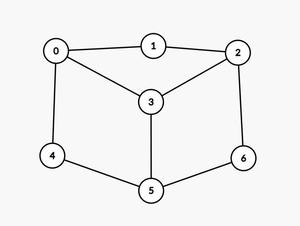
Entrada: gráfico[][] = {{0, 1, 0, 1, 1, 0, 0}, {1, 0, 1, 0, 0, 0, 0}, {0, 1, 0, 1, 0, 0, 1}, {1, 0, 1, 0, 0, 1, 0}, {1, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 1, 1, 0, 1}, {0, 0, 1, 0, 0, 1, 0}}
Salida: No es posible ningún ciclo hamiltoniano
Explicación:
Para el gráfico dado, no es posible ningún ciclo hamiltoniano:
Enfoque: el problema dado se puede resolver utilizando Backtracking para generar todos los ciclos hamiltonianos posibles. Siga los pasos a continuación para resolver el problema:
- Cree una array auxiliar , digamos ruta[] para almacenar el orden de recorrido de los Nodes y una array booleana visitada[] para realizar un seguimiento de los vértices incluidos en la ruta actual.
- Inicialmente, agregue el vértice de origen (en este caso, ‘0’) a la ruta .
- Ahora, agrega recursivamente vértices a la ruta uno por uno para encontrar el ciclo .
- Antes de agregar un vértice a la ruta , verifique si el vértice que se está considerando es adyacente al vértice agregado previamente o no y si no está ya en la ruta . Si se encuentra dicho vértice, agréguelo a la ruta y marque su valor como verdadero en la array visited[] .
- Si la longitud de la ruta se vuelve igual a N , y hay un borde desde el último vértice en la ruta a 0 , imprima la array de la ruta .
- Después de completar los pasos anteriores, si no existe tal ruta, imprima No es posible un ciclo hamiltoniano .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include<bits/stdc++.h>
using namespace std;
// To check if there exists
// at least 1 hamiltonian cycle
bool hasCycle;
// Function to check if a vertex v
// can be added at index pos in
// the Hamiltonian Cycle
bool isSafe(int v, int graph[][6], vector<int> path, int pos)
{
// If the vertex is adjacent to
// the vertex of the previously
// added vertex
if (graph[path[pos - 1]][v] == 0)
return false;
// If the vertex has already
// been included in the path
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
// Both the above conditions are
// not true, return true
return true;
}
// Recursive function to find all
// hamiltonian cycles
void FindHamCycle(int graph[][6], int pos, vector<int> path, bool visited[], int N)
{
// If all vertices are included
// in Hamiltonian Cycle
if (pos == N) {
// If there is an edge
// from the last vertex to
// the source vertex
if (graph[path[path.size() - 1]][path[0]] != 0) {
// Include source vertex
// into the path and
// print the path
path.push_back(0);
for (int i = 0; i < path.size(); i++) {
cout << path[i] << " ";
}
cout << endl;
// Remove the source
// vertex added
path.pop_back();
// Update the hasCycle
// as true
hasCycle = true;
}
return;
}
// Try different vertices
// as the next vertex
for (int v = 0; v < N; v++) {
// Check if this vertex can
// be added to Cycle
if (isSafe(v, graph, path, pos) && !visited[v]) {
path.push_back(v);
visited[v] = true;
// Recur to construct
// rest of the path
FindHamCycle(graph, pos + 1, path, visited, N);
// Remove current vertex
// from path and process
// other vertices
visited[v] = false;
path.pop_back();
}
}
}
// Function to find all possible
// hamiltonian cycles
void hamCycle(int graph[][6], int N)
{
// Initially value of boolean
// flag is false
hasCycle = false;
// Store the resultant path
vector<int> path;
path.push_back(0);
// Keeps the track of the
// visited vertices
bool visited[N];
for (int i = 0; i < N; i++)
visited[i] = false;
visited[0] = true;
// Function call to find all
// hamiltonian cycles
FindHamCycle(graph, 1, path, visited, N);
if (!hasCycle) {
// If no Hamiltonian Cycle
// is possible for the
// given graph
cout << "No Hamiltonian Cycle" << "possible " << endl;
return;
}
}
int main()
{
int graph[][6] = {
{ 0, 1, 1, 0, 0, 1 },
{ 1, 0, 1, 0, 1, 1 },
{ 1, 1, 0, 1, 0, 0 },
{ 0, 0, 1, 0, 1, 0 },
{ 0, 1, 0, 1, 0, 1 },
{ 1, 1, 0, 0, 1, 0 },
};
hamCycle(graph, 6);
return 0;
}
// This code is contributed by rameshtravel07.
Java
// Java program for the above approach
import java.util.ArrayList;
class GFG {
// Function to check if a vertex v
// can be added at index pos in
// the Hamiltonian Cycle
boolean isSafe(int v, int graph[][],
ArrayList<Integer> path,
int pos)
{
// If the vertex is adjacent to
// the vertex of the previously
// added vertex
if (graph[path.get(pos - 1)][v]
== 0)
return false;
// If the vertex has already
// been included in the path
for (int i = 0; i < pos; i++)
if (path.get(i) == v)
return false;
// Both the above conditions are
// not true, return true
return true;
}
// To check if there exists
// at least 1 hamiltonian cycle
boolean hasCycle;
// Function to find all possible
// hamiltonian cycles
void hamCycle(int graph[][])
{
// Initially value of boolean
// flag is false
hasCycle = false;
// Store the resultant path
ArrayList<Integer> path
= new ArrayList<>();
path.add(0);
// Keeps the track of the
// visited vertices
boolean[] visited
= new boolean[graph.length];
for (int i = 0;
i < visited.length; i++)
visited[i] = false;
visited[0] = true;
// Function call to find all
// hamiltonian cycles
FindHamCycle(graph, 1, path,
visited);
if (!hasCycle) {
// If no Hamiltonian Cycle
// is possible for the
// given graph
System.out.println(
"No Hamiltonian Cycle"
+ "possible ");
return;
}
}
// Recursive function to find all
// hamiltonian cycles
void FindHamCycle(int graph[][], int pos,
ArrayList<Integer> path,
boolean[] visited)
{
// If all vertices are included
// in Hamiltonian Cycle
if (pos == graph.length) {
// If there is an edge
// from the last vertex to
// the source vertex
if (graph[path.get(path.size() - 1)]
[path.get(0)]
!= 0) {
// Include source vertex
// into the path and
// print the path
path.add(0);
for (int i = 0;
i < path.size(); i++) {
System.out.print(
path.get(i) + " ");
}
System.out.println();
// Remove the source
// vertex added
path.remove(path.size() - 1);
// Update the hasCycle
// as true
hasCycle = true;
}
return;
}
// Try different vertices
// as the next vertex
for (int v = 0;
v < graph.length; v++) {
// Check if this vertex can
// be added to Cycle
if (isSafe(v, graph, path, pos)
&& !visited[v]) {
path.add(v);
visited[v] = true;
// Recur to construct
// rest of the path
FindHamCycle(
graph, pos + 1,
path, visited);
// Remove current vertex
// from path and process
// other vertices
visited[v] = false;
path.remove(
path.size() - 1);
}
}
}
// Driver Code
public static void main(String args[])
{
GFG hamiltonian = new GFG();
/* Input Graph:
(0) - - -- (2)
| \ / |
| (1) |
| / | |
| / | |
(5)----(4)--(3)*/
int[][] graph = {
{ 0, 1, 1, 0, 0, 1 },
{ 1, 0, 1, 0, 1, 1 },
{ 1, 1, 0, 1, 0, 0 },
{ 0, 0, 1, 0, 1, 0 },
{ 0, 1, 0, 1, 0, 1 },
{ 1, 1, 0, 0, 1, 0 },
};
hamiltonian.hamCycle(graph);
}
}
Python3
# Python3 program for the above approach
# Function to check if a vertex v
# can be added at index pos in
# the Hamiltonian Cycle
def isSafe(v, graph, path, pos):
# If the vertex is adjacent to
# the vertex of the previously
# added vertex
if graph[path[pos - 1]][v] == 0:
return False
# If the vertex has already
# been included in the path
for i in range(pos):
if path[i] == v:
return False
# Both the above conditions are
# not true, return true
return True
# To check if there exists
# at least 1 hamiltonian cycle
hasCycle = False
# Function to find all possible
# hamiltonian cycles
def hamCycle(graph):
global hasCycle
# Initially value of boolean
# flag is false
hasCycle = False
# Store the resultant path
path = []
path.append(0)
# Keeps the track of the
# visited vertices
visited = [False]*(len(graph))
for i in range(len(visited)):
visited[i] = False
visited[0] = True
# Function call to find all
# hamiltonian cycles
FindHamCycle(graph, 1, path, visited)
if hasCycle:
# If no Hamiltonian Cycle
# is possible for the
# given graph
print("No Hamiltonian Cycle" + "possible ")
return
# Recursive function to find all
# hamiltonian cycles
def FindHamCycle(graph, pos, path, visited):
# If all vertices are included
# in Hamiltonian Cycle
if pos == len(graph):
# If there is an edge
# from the last vertex to
# the source vertex
if graph[path[-1]][path[0]] != 0:
# Include source vertex
# into the path and
# print the path
path.append(0)
for i in range(len(path)):
print(path[i], end = " ")
print()
# Remove the source
# vertex added
path.pop()
# Update the hasCycle
# as true
hasCycle = True
return
# Try different vertices
# as the next vertex
for v in range(len(graph)):
# Check if this vertex can
# be added to Cycle
if isSafe(v, graph, path, pos) and not visited[v]:
path.append(v)
visited[v] = True
# Recur to construct
# rest of the path
FindHamCycle(graph, pos + 1, path, visited)
# Remove current vertex
# from path and process
# other vertices
visited[v] = False
path.pop()
""" Input Graph:
(0) - - -- (2)
| \ / |
| (1) |
| / | |
| / | |
(5)----(4)--(3)"""
graph = [
[ 0, 1, 1, 0, 0, 1 ],
[ 1, 0, 1, 0, 1, 1 ],
[ 1, 1, 0, 1, 0, 0 ],
[ 0, 0, 1, 0, 1, 0 ],
[ 0, 1, 0, 1, 0, 1 ],
[ 1, 1, 0, 0, 1, 0 ],
]
hamCycle(graph)
# This code is contributed by divyesh072019.
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG {
// Function to check if a vertex v
// can be added at index pos in
// the Hamiltonian Cycle
static bool isSafe(int v, int[,] graph, List<int> path, int pos)
{
// If the vertex is adjacent to
// the vertex of the previously
// added vertex
if (graph[path[pos - 1],v] == 0)
return false;
// If the vertex has already
// been included in the path
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
// Both the above conditions are
// not true, return true
return true;
}
// To check if there exists
// at least 1 hamiltonian cycle
static bool hasCycle;
// Function to find all possible
// hamiltonian cycles
static void hamCycle(int[,] graph)
{
// Initially value of boolean
// flag is false
hasCycle = false;
// Store the resultant path
List<int> path = new List<int>();
path.Add(0);
// Keeps the track of the
// visited vertices
bool[] visited = new bool[graph.GetLength(0)];
for (int i = 0; i < visited.Length; i++)
visited[i] = false;
visited[0] = true;
// Function call to find all
// hamiltonian cycles
FindHamCycle(graph, 1, path, visited);
if (!hasCycle) {
// If no Hamiltonian Cycle
// is possible for the
// given graph
Console.WriteLine("No Hamiltonian Cycle" + "possible ");
return;
}
}
// Recursive function to find all
// hamiltonian cycles
static void FindHamCycle(int[,] graph, int pos, List<int> path, bool[] visited)
{
// If all vertices are included
// in Hamiltonian Cycle
if (pos == graph.GetLength(0)) {
// If there is an edge
// from the last vertex to
// the source vertex
if (graph[path[path.Count - 1], path[0]] != 0) {
// Include source vertex
// into the path and
// print the path
path.Add(0);
for (int i = 0; i < path.Count; i++) {
Console.Write(path[i] + " ");
}
Console.WriteLine();
// Remove the source
// vertex added
path.RemoveAt(path.Count - 1);
// Update the hasCycle
// as true
hasCycle = true;
}
return;
}
// Try different vertices
// as the next vertex
for (int v = 0; v < graph.GetLength(0); v++) {
// Check if this vertex can
// be added to Cycle
if (isSafe(v, graph, path, pos) && !visited[v]) {
path.Add(v);
visited[v] = true;
// Recur to construct
// rest of the path
FindHamCycle(graph, pos + 1, path, visited);
// Remove current vertex
// from path and process
// other vertices
visited[v] = false;
path.RemoveAt(path.Count - 1);
}
}
}
static void Main() {
/* Input Graph:
(0) - - -- (2)
| \ / |
| (1) |
| / | |
| / | |
(5)----(4)--(3)*/
int[,] graph = {
{ 0, 1, 1, 0, 0, 1 },
{ 1, 0, 1, 0, 1, 1 },
{ 1, 1, 0, 1, 0, 0 },
{ 0, 0, 1, 0, 1, 0 },
{ 0, 1, 0, 1, 0, 1 },
{ 1, 1, 0, 0, 1, 0 },
};
hamCycle(graph);
}
}
// This code is contributed by suresh07.
Javascript
<script>
// Javascript program for the above approach
// Function to check if a vertex v
// can be added at index pos in
// the Hamiltonian Cycle
function isSafe(v, graph, path, pos)
{
// If the vertex is adjacent to
// the vertex of the previously
// added vertex
if (graph[path[pos - 1]][v] == 0)
return false;
// If the vertex has already
// been included in the path
for (let i = 0; i < pos; i++)
if (path[i] == v)
return false;
// Both the above conditions are
// not true, return true
return true;
}
// To check if there exists
// at least 1 hamiltonian cycle
let hasCycle;
// Function to find all possible
// hamiltonian cycles
function hamCycle(graph)
{
// Initially value of boolean
// flag is false
hasCycle = false;
// Store the resultant path
let path = [];
path.push(0);
// Keeps the track of the
// visited vertices
let visited = new Array(graph.length);
for (let i = 0; i < visited.length; i++)
visited[i] = false;
visited[0] = true;
// Function call to find all
// hamiltonian cycles
FindHamCycle(graph, 1, path, visited);
if (!hasCycle) {
// If no Hamiltonian Cycle
// is possible for the
// given graph
document.write("No Hamiltonian Cycle" + "possible ");
return;
}
}
// Recursive function to find all
// hamiltonian cycles
function FindHamCycle(graph, pos, path, visited)
{
// If all vertices are included
// in Hamiltonian Cycle
if (pos == graph.length) {
// If there is an edge
// from the last vertex to
// the source vertex
if (graph[path[path.length - 1]][path[0]] != 0) {
// Include source vertex
// into the path and
// print the path
path.push(0);
for (let i = 0; i < path.length; i++) {
document.write(path[i] + " ");
}
document.write("</br>");
// Remove the source
// vertex added
path.pop();
// Update the hasCycle
// as true
hasCycle = true;
}
return;
}
// Try different vertices
// as the next vertex
for (let v = 0; v < graph.length; v++) {
// Check if this vertex can
// be added to Cycle
if (isSafe(v, graph, path, pos) && !visited[v]) {
path.push(v);
visited[v] = true;
// Recur to construct
// rest of the path
FindHamCycle(graph, pos + 1, path, visited);
// Remove current vertex
// from path and process
// other vertices
visited[v] = false;
path.pop();
}
}
}
/* Input Graph:
(0) - - -- (2)
| \ / |
| (1) |
| / | |
| / | |
(5)----(4)--(3)*/
let graph = [
[ 0, 1, 1, 0, 0, 1 ],
[ 1, 0, 1, 0, 1, 1 ],
[ 1, 1, 0, 1, 0, 0 ],
[ 0, 0, 1, 0, 1, 0 ],
[ 0, 1, 0, 1, 0, 1 ],
[ 1, 1, 0, 0, 1, 0 ],
];
hamCycle(graph);
// This code is contributed by divyeshrabadiya07.
</script>
0 1 2 3 4 5 0 0 1 5 4 3 2 0 0 2 3 4 1 5 0 0 2 3 4 5 1 0 0 5 1 4 3 2 0 0 5 4 3 2 1 0
Complejidad temporal: O(N!)
Espacio auxiliar: O(N)