Dado un árbol binario, un Node objetivo en el árbol binario y un valor entero k, imprima todos los Nodes que están a una distancia k del Node objetivo dado. No hay punteros principales disponibles.
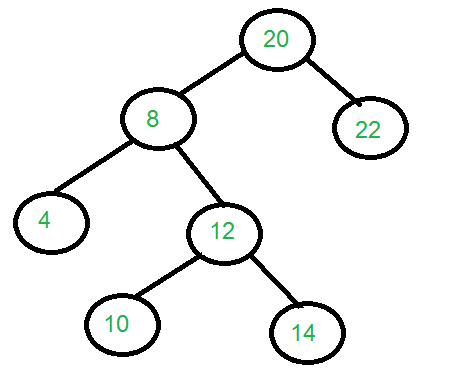
Considere el árbol que se muestra en el diagrama
Entrada: objetivo = puntero al Node con datos 8.
raíz = puntero al Node con datos 20.
k = 2.
Salida: 10 14 22
Si el objetivo es 14 y k es 3, entonces la salida
debe ser “4 20”
Hay dos tipos de Nodes a considerar.
1) Nodes en el subárbol enraizados con el Node de destino. Por ejemplo, si el Node de destino es 8 yk es 2, entonces dichos Nodes son 10 y 14.
2) Otros Nodes pueden ser un ancestro de destino o un Node en algún otro subárbol. Para el Node de destino 8 y k es 2, el Node 22 entra en esta categoría.
Encontrar el primer tipo de Nodes es fácil de implementar. Simplemente atraviese los subárboles enraizados con el Node de destino y disminuya k en la llamada recursiva. Cuando k se convierte en 0, imprime el Node que se está atravesando actualmente (ver esto para más detalles). Aquí llamamos a la función como printkdistanceNodeDown() .
¿Cómo encontrar Nodes de segundo tipo? Para los Nodes de salida que no se encuentran en el subárbol con el Node de destino como raíz, debemos pasar por todos los ancestros. Para cada ancestro, encontramos su distancia desde el Node objetivo, dejemos que la distancia sea d, ahora vamos a otro subárbol (si el objetivo se encontró en el subárbol izquierdo, luego vamos al subárbol derecho y viceversa) del ancestro y buscamos todos los Nodes a kd distancia del antepasado.
A continuación se muestra la implementación del enfoque anterior.
C++
#include <iostream>
using namespace std;
// A binary Tree node
struct node
{
int data;
struct node *left, *right;
};
/* Recursive function to print all the nodes at distance k in the
tree (or subtree) rooted with given root. See */
void printkdistanceNodeDown(node *root, int k)
{
// Base Case
if (root == NULL || k < 0) return;
// If we reach a k distant node, print it
if (k==0)
{
cout << root->data << endl;
return;
}
// Recur for left and right subtrees
printkdistanceNodeDown(root->left, k-1);
printkdistanceNodeDown(root->right, k-1);
}
// Prints all nodes at distance k from a given target node.
// The k distant nodes may be upward or downward. This function
// Returns distance of root from target node, it returns -1 if target
// node is not present in tree rooted with root.
int printkdistanceNode(node* root, node* target , int k)
{
// Base Case 1: If tree is empty, return -1
if (root == NULL) return -1;
// If target is same as root. Use the downward function
// to print all nodes at distance k in subtree rooted with
// target or root
if (root == target)
{
printkdistanceNodeDown(root, k);
return 0;
}
// Recur for left subtree
int dl = printkdistanceNode(root->left, target, k);
// Check if target node was found in left subtree
if (dl != -1)
{
// If root is at distance k from target, print root
// Note that dl is Distance of root's left child from target
if (dl + 1 == k)
cout << root->data << endl;
// Else go to right subtree and print all k-dl-2 distant nodes
// Note that the right child is 2 edges away from left child
else
printkdistanceNodeDown(root->right, k-dl-2);
// Add 1 to the distance and return value for parent calls
return 1 + dl;
}
// MIRROR OF ABOVE CODE FOR RIGHT SUBTREE
// Note that we reach here only when node was not found in left subtree
int dr = printkdistanceNode(root->right, target, k);
if (dr != -1)
{
if (dr + 1 == k)
cout << root->data << endl;
else
printkdistanceNodeDown(root->left, k-dr-2);
return 1 + dr;
}
// If target was neither present in left nor in right subtree
return -1;
}
// A utility function to create a new binary tree node
node *newnode(int data)
{
node *temp = new node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// Driver program to test above functions
int main()
{
/* Let us construct the tree shown in above diagram */
node * root = newnode(20);
root->left = newnode(8);
root->right = newnode(22);
root->left->left = newnode(4);
root->left->right = newnode(12);
root->left->right->left = newnode(10);
root->left->right->right = newnode(14);
node * target = root->left->right;
printkdistanceNode(root, target, 2);
return 0;
}
Java
// Java program to print all nodes at a distance k from given node
// A binary tree node
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree
{
Node root;
/* Recursive function to print all the nodes at distance k in
tree (or subtree) rooted with given root. */
void printkdistanceNodeDown(Node node, int k)
{
// Base Case
if (node == null || k < 0)
return;
// If we reach a k distant node, print it
if (k == 0)
{
System.out.print(node.data);
System.out.println("");
return;
}
// Recur for left and right subtrees
printkdistanceNodeDown(node.left, k - 1);
printkdistanceNodeDown(node.right, k - 1);
}
// Prints all nodes at distance k from a given target node.
// The k distant nodes may be upward or downward.This function
// Returns distance of root from target node, it returns -1
// if target node is not present in tree rooted with root.
int printkdistanceNode(Node node, Node target, int k)
{
// Base Case 1: If tree is empty, return -1
if (node == null)
return -1;
// If target is same as root. Use the downward function
// to print all nodes at distance k in subtree rooted with
// target or root
if (node == target)
{
printkdistanceNodeDown(node, k);
return 0;
}
// Recur for left subtree
int dl = printkdistanceNode(node.left, target, k);
// Check if target node was found in left subtree
if (dl != -1)
{
// If root is at distance k from target, print root
// Note that dl is Distance of root's left child from
// target
if (dl + 1 == k)
{
System.out.print(node.data);
System.out.println("");
}
// Else go to right subtree and print all k-dl-2 distant nodes
// Note that the right child is 2 edges away from left child
else
printkdistanceNodeDown(node.right, k - dl - 2);
// Add 1 to the distance and return value for parent calls
return 1 + dl;
}
// MIRROR OF ABOVE CODE FOR RIGHT SUBTREE
// Note that we reach here only when node was not found in left
// subtree
int dr = printkdistanceNode(node.right, target, k);
if (dr != -1)
{
if (dr + 1 == k)
{
System.out.print(node.data);
System.out.println("");
}
else
printkdistanceNodeDown(node.left, k - dr - 2);
return 1 + dr;
}
// If target was neither present in left nor in right subtree
return -1;
}
// Driver program to test the above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
/* Let us construct the tree shown in above diagram */
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
Node target = tree.root.left.right;
tree.printkdistanceNode(tree.root, target, 2);
}
}
// This code has been contributed by Mayank Jaiswal
Python3
# Python program to print nodes at distance k from a given node # A binary tree node class Node: # A constructor to create a new node def __init__(self, data): self.data = data self.left = None self.right = None # Recursive function to print all the nodes at distance k # int the tree(or subtree) rooted with given root. See def printkDistanceNodeDown(root, k): # Base Case if root is None or k< 0 : return # If we reach a k distant node, print it if k == 0 : print (root.data) return # Recur for left and right subtree printkDistanceNodeDown(root.left, k-1) printkDistanceNodeDown(root.right, k-1) # Prints all nodes at distance k from a given target node # The k distant nodes may be upward or downward. This function # returns distance of root from target node, it returns -1 # if target node is not present in tree rooted with root def printkDistanceNode(root, target, k): # Base Case 1 : IF tree is empty return -1 if root is None: return -1 # If target is same as root. Use the downward function # to print all nodes at distance k in subtree rooted with # target or root if root == target: printkDistanceNodeDown(root, k) return 0 # Recur for left subtree dl = printkDistanceNode(root.left, target, k) # Check if target node was found in left subtree if dl != -1: # If root is at distance k from target, print root # Note: dl is distance of root's left child # from target if dl +1 == k : print (root.data) # Else go to right subtree and print all k-dl-2 # distant nodes # Note: that the right child is 2 edges away from # left child else: printkDistanceNodeDown(root.right, k-dl-2) # Add 1 to the distance and return value for # for parent calls return 1 + dl # MIRROR OF ABOVE CODE FOR RIGHT SUBTREE # Note that we reach here only when node was not found # in left subtree dr = printkDistanceNode(root.right, target, k) if dr != -1: if (dr+1 == k): print (root.data) else: printkDistanceNodeDown(root.left, k-dr-2) return 1 + dr # If target was neither present in left nor in right subtree return -1 # Driver program to test above function root = Node(20) root.left = Node(8) root.right = Node(22) root.left.left = Node(4) root.left.right = Node(12) root.left.right.left = Node(10) root.left.right.right = Node(14) target = root.left.right printkDistanceNode(root, target, 2) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
using System;
// C# program to print all nodes at a distance k from given node
// A binary tree node
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
public Node root;
/* Recursive function to print all the nodes at distance k in
tree (or subtree) rooted with given root. */
public virtual void printkdistanceNodeDown(Node node, int k)
{
// Base Case
if (node == null || k < 0)
{
return;
}
// If we reach a k distant node, print it
if (k == 0)
{
Console.Write(node.data);
Console.WriteLine("");
return;
}
// Recur for left and right subtrees
printkdistanceNodeDown(node.left, k - 1);
printkdistanceNodeDown(node.right, k - 1);
}
// Prints all nodes at distance k from a given target node.
// The k distant nodes may be upward or downward.This function
// Returns distance of root from target node, it returns -1
// if target node is not present in tree rooted with root.
public virtual int printkdistanceNode(Node node, Node target, int k)
{
// Base Case 1: If tree is empty, return -1
if (node == null)
{
return -1;
}
// If target is same as root. Use the downward function
// to print all nodes at distance k in subtree rooted with
// target or root
if (node == target)
{
printkdistanceNodeDown(node, k);
return 0;
}
// Recur for left subtree
int dl = printkdistanceNode(node.left, target, k);
// Check if target node was found in left subtree
if (dl != -1)
{
// If root is at distance k from target, print root
// Note that dl is Distance of root's left child from
// target
if (dl + 1 == k)
{
Console.Write(node.data);
Console.WriteLine("");
}
// Else go to right subtree and print all k-dl-2 distant nodes
// Note that the right child is 2 edges away from left child
else
{
printkdistanceNodeDown(node.right, k - dl - 2);
}
// Add 1 to the distance and return value for parent calls
return 1 + dl;
}
// MIRROR OF ABOVE CODE FOR RIGHT SUBTREE
// Note that we reach here only when node was not found in left
// subtree
int dr = printkdistanceNode(node.right, target, k);
if (dr != -1)
{
if (dr + 1 == k)
{
Console.Write(node.data);
Console.WriteLine("");
}
else
{
printkdistanceNodeDown(node.left, k - dr - 2);
}
return 1 + dr;
}
// If target was neither present in left nor in right subtree
return -1;
}
// Driver program to test the above functions
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
/* Let us construct the tree shown in above diagram */
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
Node target = tree.root.left.right;
tree.printkdistanceNode(tree.root, target, 2);
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// Javascript program to print all nodes at a distance k from given node
// A binary tree node
class Node
{
constructor(item)
{
this.data = item;
this.left = null;
this.right = null;
}
}
var root = null;
/* Recursive function to print all the nodes at distance k in
tree (or subtree) rooted with given root. */
function printkdistanceNodeDown(node, k)
{
// Base Case
if (node == null || k < 0)
{
return;
}
// If we reach a k distant node, print it
if (k == 0)
{
document.write(node.data);
document.write("<br>");
return;
}
// Recur for left and right subtrees
printkdistanceNodeDown(node.left, k - 1);
printkdistanceNodeDown(node.right, k - 1);
}
// Prints all nodes at distance k from a given target node.
// The k distant nodes may be upward or downward.This function
// Returns distance of root from target node, it returns -1
// if target node is not present in tree rooted with root.
function printkdistanceNode(node, target, k)
{
// Base Case 1: If tree is empty, return -1
if (node == null)
{
return -1;
}
// If target is same as root. Use the downward function
// to print all nodes at distance k in subtree rooted with
// target or root
if (node == target)
{
printkdistanceNodeDown(node, k);
return 0;
}
// Recur for left subtree
var dl = printkdistanceNode(node.left, target, k);
// Check if target node was found in left subtree
if (dl != -1)
{
// If root is at distance k from target, print root
// Note that dl is Distance of root's left child from
// target
if (dl + 1 == k)
{
document.write(node.data);
document.write("<br>");
}
// Else go to right subtree and print all k-dl-2 distant nodes
// Note that the right child is 2 edges away from left child
else
{
printkdistanceNodeDown(node.right, k - dl - 2);
}
// Add 1 to the distance and return value for parent calls
return 1 + dl;
}
// MIRROR OF ABOVE CODE FOR RIGHT SUBTREE
// Note that we reach here only when node was not found in left
// subtree
var dr = printkdistanceNode(node.right, target, k);
if (dr != -1)
{
if (dr + 1 == k)
{
document.write(node.data);
document.write("<br>");
}
else
{
printkdistanceNodeDown(node.left, k - dr - 2);
}
return 1 + dr;
}
// If target was neither present in left nor in right subtree
return -1;
}
// Driver program to test the above functions
/* Let us construct the tree shown in above diagram */
root = new Node(20);
root.left = new Node(8);
root.right = new Node(22);
root.left.left = new Node(4);
root.left.right = new Node(12);
root.left.right.left = new Node(10);
root.left.right.right = new Node(14);
var target = root.left.right;
printkdistanceNode(root, target, 2);
// This code is contributed by importantly.
</script>
Producción:
4 20
Complejidad del tiempo: A primera vista, la complejidad del tiempo parece más que O(n), pero si miramos más de cerca, podemos observar que ningún Node se recorre más de dos veces. Por lo tanto, la complejidad del tiempo es O(n).
Este artículo es una contribución de Prasant Kumar . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Solución alternativa:
- Obtenga la ruta del Node raíz y agréguela a una lista
- Para cada i-ésimo elemento de Path, solo itere e imprima (Ki)-ésimos Nodes de distancia.
Java
import java.io.*;
import java.util.*;
class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode() {}
public TreeNode(int val) { this.val = val; }
}
class GFG {
List<TreeNode> path = null;
//Finding all the nodes at a distance K from target
//node.
public List<Integer> distanceK(TreeNode root,
TreeNode target, int K)
{
path = new ArrayList<>();
findPath(root, target);
List<Integer> result = new ArrayList<>();
for (int i = 0; i < path.size(); i++) {
findKDistanceFromNode(
path.get(i), K - i, result,
i == 0 ? null : path.get(i - 1));
}
//Returning list of all nodes at a distance K
return result;
}
// Blocker is used for ancestors node if target at
//left then we have to go in right or if target at
// right then we have to go in left.
public void findKDistanceFromNode(TreeNode node,
int dist,
List<Integer> result,
TreeNode blocker)
{
if (dist < 0 || node == null
|| (blocker != null && node == blocker)) {
return;
}
if (dist == 0) {
result.add(node.val);
}
findKDistanceFromNode(node.left, dist - 1, result,
blocker);
findKDistanceFromNode(node.right, dist - 1, result,
blocker);
}
//Finding the path of target node from root node
public boolean findPath(TreeNode node, TreeNode target)
{
if (node == null)
return false;
if (node == target || findPath(node.left, target)
|| findPath(node.right, target)) {
path.add(node);
return true;
}
return false;
}
// Driver program to test the above functions
public static void main(String[] args)
{
GFG gfg = new GFG();
/* Let us construct the tree shown in above diagram */
TreeNode root = new TreeNode(20);
root.left = new TreeNode(8);
root.right = new TreeNode(22);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(12);
root.left.right.left = new TreeNode(10);
root.left.right.right = new TreeNode(14);
TreeNode target = root.left.right;
System.out.println(gfg.distanceK(root, target, 2));
}
}
[4, 20]
Complejidad de tiempo: O(n)
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA