Dado un árbol binario y un entero positivo k, imprima todos los Nodes que estén a una distancia k de un Node hoja.
Aquí el significado de la distancia es diferente de la publicación anterior . Aquí k distancia desde una hoja significa k niveles más altos que un Node hoja. Por ejemplo, si k es mayor que la altura del árbol binario, entonces no se debe imprimir nada. La complejidad de tiempo esperada es O(n) donde n es el número de Nodes en el árbol binario dado.
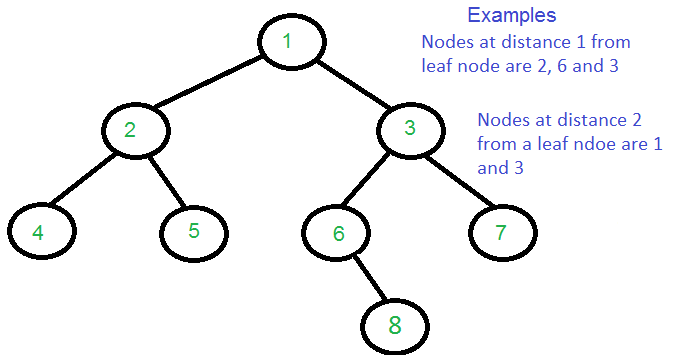
La idea es atravesar el árbol. Siga almacenando todos los ancestros hasta que lleguemos a un Node de hoja. Cuando llegamos a un Node hoja, imprimimos el ancestro a la distancia k. También necesitamos realizar un seguimiento de los Nodes que ya están impresos como salida. Para eso usamos una array booleana visited[].
C++
/* Program to print all nodes
which are at distance k from a leaf */
#include <iostream>
using namespace std;
#define MAX_HEIGHT 10000
struct Node {
int key;
Node *left, *right;
};
/* utility that allocates a new Node with the given key */
Node* newNode(int key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return (node);
}
/* This function prints all nodes that are distance k from a leaf node
path[] --> Store ancestors of a node
visited[] --> Stores true if a node is printed as output. A node may be k
distance away from many leaves, we want to print it once */
void kDistantFromLeafUtil(Node* node, int path[], bool visited[],
int pathLen, int k)
{
// Base case
if (node == NULL)
return;
/* append this Node to the path array */
path[pathLen] = node->key;
visited[pathLen] = false;
pathLen++;
/* it's a leaf, so print the ancestor at distance k only
if the ancestor is not already printed */
if (node->left == NULL &&
node->right == NULL &&
pathLen - k - 1 >= 0 &&
visited[pathLen - k - 1] == false)
{
cout << path[pathLen - k - 1] << " ";
visited[pathLen - k - 1] = true;
return;
}
/* If not leaf node, recur for left and right subtrees */
kDistantFromLeafUtil(node->left, path, visited, pathLen, k);
kDistantFromLeafUtil(node->right, path, visited, pathLen, k);
}
/* Given a binary tree and a number k, print all nodes that are k
distant from a leaf*/
void printKDistantfromLeaf(Node* node, int k)
{
int path[MAX_HEIGHT];
bool visited[MAX_HEIGHT] = { false };
kDistantFromLeafUtil(node, path, visited, 0, k);
}
/* Driver code*/
int main()
{
// Let us create binary tree
// given in the above example
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
cout << "Nodes at distance 2 are: ";
printKDistantfromLeaf(root, 2);
return 0;
}
Java
// Java program to print all nodes at a distance k from leaf
// A binary tree node
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
Node root;
/* This function prints all nodes that are distance k from a leaf node
path[] --> Store ancestors of a node
visited[] --> Stores true if a node is printed as output. A node may
be k distance away from many leaves, we want to print it once */
void kDistantFromLeafUtil(Node node, int path[], boolean visited[],
int pathLen, int k)
{
// Base case
if (node == null)
return;
/* append this Node to the path array */
path[pathLen] = node.data;
visited[pathLen] = false;
pathLen++;
/* it's a leaf, so print the ancestor at distance k only
if the ancestor is not already printed */
if (node.left == null && node.right == null
&& pathLen - k - 1 >= 0 && visited[pathLen - k - 1] == false) {
System.out.print(path[pathLen - k - 1] + " ");
visited[pathLen - k - 1] = true;
return;
}
/* If not leaf node, recur for left and right subtrees */
kDistantFromLeafUtil(node.left, path, visited, pathLen, k);
kDistantFromLeafUtil(node.right, path, visited, pathLen, k);
}
/* Given a binary tree and a number k, print all nodes that are k
distant from a leaf*/
void printKDistantfromLeaf(Node node, int k)
{
int path[] = new int[1000];
boolean visited[] = new boolean[1000];
kDistantFromLeafUtil(node, path, visited, 0, k);
}
// Driver program to test the above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
/* Let us construct the tree shown in above diagram */
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
System.out.println(" Nodes at distance 2 are :");
tree.printKDistantfromLeaf(tree.root, 2);
}
}
// This code has been contributed by Mayank Jaiswal
Python3
# Program to print all nodes which are at
# distance k from a leaf
# utility that allocates a new Node with
# the given key
class newNode:
def __init__(self, key):
self.key = key
self.left = self.right = None
# This function prints all nodes that
# are distance k from a leaf node
# path[] -. Store ancestors of a node
# visited[] -. Stores true if a node is
# printed as output. A node may be k distance
# away from many leaves, we want to print it once
def kDistantFromLeafUtil(node, path, visited,
pathLen, k):
# Base case
if (node == None):
return
# append this Node to the path array
path[pathLen] = node.key
visited[pathLen] = False
pathLen += 1
# it's a leaf, so print the ancestor at
# distance k only if the ancestor is
# not already printed
if (node.left == None and node.right == None and
pathLen - k - 1 >= 0 and
visited[pathLen - k - 1] == False):
print(path[pathLen - k - 1], end = " ")
visited[pathLen - k - 1] = True
return
# If not leaf node, recur for left
# and right subtrees
kDistantFromLeafUtil(node.left, path,
visited, pathLen, k)
kDistantFromLeafUtil(node.right, path,
visited, pathLen, k)
# Given a binary tree and a number k,
# print all nodes that are k distant from a leaf
def printKDistantfromLeaf(node, k):
global MAX_HEIGHT
path = [None] * MAX_HEIGHT
visited = [False] * MAX_HEIGHT
kDistantFromLeafUtil(node, path, visited, 0, k)
# Driver Code
MAX_HEIGHT = 10000
# Let us create binary tree given in
# the above example
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
root.right.left = newNode(6)
root.right.right = newNode(7)
root.right.left.right = newNode(8)
print("Nodes at distance 2 are:", end = " ")
printKDistantfromLeaf(root, 2)
# This code is contributed by pranchalK
C#
using System;
// C# program to print all nodes at a distance k from leaf
// A binary tree node
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree {
public Node root;
/* This function prints all nodes that are distance k from a leaf node
path[] --> Store ancestors of a node
visited[] --> Stores true if a node is printed as output. A node may
be k distance away from many leaves, we want to print it once */
public virtual void kDistantFromLeafUtil(Node node, int[] path, bool[] visited, int pathLen, int k)
{
// Base case
if (node == null) {
return;
}
/* append this Node to the path array */
path[pathLen] = node.data;
visited[pathLen] = false;
pathLen++;
/* it's a leaf, so print the ancestor at distance k only
if the ancestor is not already printed */
if (node.left == null && node.right == null && pathLen - k - 1 >= 0 && visited[pathLen - k - 1] == false) {
Console.Write(path[pathLen - k - 1] + " ");
visited[pathLen - k - 1] = true;
return;
}
/* If not leaf node, recur for left and right subtrees */
kDistantFromLeafUtil(node.left, path, visited, pathLen, k);
kDistantFromLeafUtil(node.right, path, visited, pathLen, k);
}
/* Given a binary tree and a number k, print all nodes that are k
distant from a leaf*/
public virtual void printKDistantfromLeaf(Node node, int k)
{
int[] path = new int[1000];
bool[] visited = new bool[1000];
kDistantFromLeafUtil(node, path, visited, 0, k);
}
// Driver program to test the above functions
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
/* Let us construct the tree shown in above diagram */
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
Console.WriteLine(" Nodes at distance 2 are :");
tree.printKDistantfromLeaf(tree.root, 2);
}
}
// This code is contributed by Shrikant13
Javascript
<script>
// JavaScript program to print all
// nodes at a distance k from leaf
// A binary tree node
class Node
{
constructor(item) {
this.left = null;
this.right = null;
this.data = item;
}
}
let root;
/* This function prints all nodes that
are distance k from a leaf node
path[] --> Store ancestors of a node
visited[] --> Stores true if a node is
printed as output. A node may
be k distance away from many leaves,
we want to print it once */
function kDistantFromLeafUtil(node, path, visited, pathLen, k)
{
// Base case
if (node == null)
return;
/* append this Node to the path array */
path[pathLen] = node.data;
visited[pathLen] = false;
pathLen++;
/* it's a leaf, so print the ancestor at distance k only
if the ancestor is not already printed */
if (node.left == null && node.right == null
&& (pathLen - k - 1) >= 0 &&
visited[pathLen - k - 1] == false) {
document.write(path[pathLen - k - 1] + " ");
visited[pathLen - k - 1] = true;
return;
}
/* If not leaf node, recur for left and right subtrees */
kDistantFromLeafUtil(node.left, path, visited, pathLen, k);
kDistantFromLeafUtil(node.right, path, visited, pathLen, k);
}
/* Given a binary tree and a number k, print all nodes that are k
distant from a leaf*/
function printKDistantfromLeaf(node, k)
{
let path = new Array(1000);
path.fill(0);
let visited = new Array(1000);
visited.fill(false);
kDistantFromLeafUtil(node, path, visited, 0, k);
}
/* Let us construct the tree shown in above diagram */
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
document.write(" Nodes at distance 2 are : ");
printKDistantfromLeaf(root, 2);
</script>
Nodes at distance 2 are: 1 3
Complejidad de tiempo: la complejidad de tiempo del código anterior es O (n) ya que el código realiza un recorrido de árbol simple.
Solución de espacio optimizado:
C++
// C++ program to print all nodes at a distance k from leaf
// A binary tree node
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int data;
Node *left, *right;
};
// Utility function to
// create a new tree node
Node* newNode(int key)
{
Node *temp = new Node;
temp->data= key;
temp->left = temp->right = NULL;
return temp;
}
/* Given a binary tree and a number k,
print all nodes that are k
distant from a leaf*/
int printKDistantfromLeaf(struct Node *node, int k)
{
if (node == NULL)
return -1;
int lk = printKDistantfromLeaf(node->left, k);
int rk = printKDistantfromLeaf(node->right, k);
bool isLeaf = lk == -1 && lk == rk;
if (lk == 0 || rk == 0 || (isLeaf && k == 0))
cout<<(" " )<<( node->data);
if (isLeaf && k > 0)
return k - 1; // leaf node
if (lk > 0 && lk < k)
return lk - 1; // parent of left leaf
if (rk > 0 && rk < k)
return rk - 1; // parent of right leaf
return -2;
}
// Driver code
int main()
{
Node *root = NULL;
/* Let us construct the tree shown in above diagram */
root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
cout << (" Nodes at distance 2 are :") << endl;
printKDistantfromLeaf(root, 2);
}
// This code contributed by aashish1995
Java
// Java program to print all nodes at a distance k from leaf
// A binary tree node
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
Node root;
/* Given a binary tree and a number k, print all nodes that are k
distant from a leaf*/
int printKDistantfromLeaf(Node node, int k)
{
if (node == null)
return -1;
int lk = printKDistantfromLeaf(node.left, k);
int rk = printKDistantfromLeaf(node.right, k);
boolean isLeaf = lk == -1 && lk == rk;
if (lk == 0 || rk == 0 || (isLeaf && k == 0))
System.out.print(" " + node.data);
if (isLeaf && k > 0)
return k - 1; // leaf node
if (lk > 0 && lk < k)
return lk - 1; // parent of left leaf
if (rk > 0 && rk < k)
return rk - 1; // parent of right leaf
return -2;
}
// Driver program to test the above functions
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
/* Let us construct the tree shown in above diagram */
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
System.out.println(" Nodes at distance 2 are :");
tree.printKDistantfromLeaf(tree.root, 2);
}
}
// This code has been contributed by Vijayan Annamalai
Python3
# Python program to print all nodes
# at a distance k from leaf
# A binary tree node
class Node:
def __init__(self,item):
self.data = item
self.left = None
self.right = None
class BinaryTree:
def __init__(self):
self.root = None
# Given a binary tree and a number
# k, print all nodes that are k
# distant from a leaf
def printKDistantfromLeaf(self,node, k):
if (node == None):
return -1
lk = self.printKDistantfromLeaf(node.left, k)
rk = self.printKDistantfromLeaf(node.right, k)
isLeaf = lk == -1 and lk == rk
if (lk == 0 or rk == 0 or (isLeaf and k == 0)):
print(node.data,end=" ")
# Leaf node
if (isLeaf and k > 0):
return k - 1
# Parent of left leaf
if (lk > 0 and lk < k):
return lk - 1
# Parent of right leaf
if (rk > 0 and rk < k):
return rk - 1
return -2
# Driver code
tree = BinaryTree()
# Let us construct the tree shown
# in above diagram
tree.root = Node(1)
tree.root.left = Node(2)
tree.root.right = Node(3)
tree.root.left.left = Node(4)
tree.root.left.right = Node(5)
tree.root.right.left = Node(6)
tree.root.right.right = Node(7)
tree.root.right.left.right = Node(8)
print("Nodes at distance 2 are :")
tree.printKDistantfromLeaf(tree.root, 2)
# self code is contributed by shinjanpatra
C#
// C# program to print all nodes at a distance k from leaf
// A binary tree node
using System;
class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
Node root;
/* Given a binary tree and a number k, print all nodes that are k
distant from a leaf*/
int printKDistantfromLeaf(Node node, int k)
{
if (node == null)
return -1;
int lk = printKDistantfromLeaf(node.left, k);
int rk = printKDistantfromLeaf(node.right, k);
bool isLeaf = lk == -1 && lk == rk;
if (lk == 0 || rk == 0 || (isLeaf && k == 0))
Console.Write(" " + node.data);
if (isLeaf && k > 0)
return k - 1; // leaf node
if (lk > 0 && lk < k)
return lk - 1; // parent of left leaf
if (rk > 0 && rk < k)
return rk - 1; // parent of right leaf
return -2;
}
// Driver program to test the above functions
public static void Main(string []args)
{
BinaryTree tree = new BinaryTree();
/* Let us construct the tree shown in above diagram */
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
Console.Write("Nodes at distance 2 are :");
tree.printKDistantfromLeaf(tree.root, 2);
}
}
// This code is contributed by rutvik_56
Javascript
<script>
// JavaScript program to print all nodes
// at a distance k from leaf
// A binary tree node
class Node
{
constructor(item)
{
this.data = item;
this.left = null;
this.right = null;
}
}
class BinaryTree
{
constructor()
{
this.root = null;
}
// Given a binary tree and a number
// k, print all nodes that are k
// distant from a leaf
printKDistantfromLeaf(node, k)
{
if (node == null)
return -1;
var lk = this.printKDistantfromLeaf(node.left, k);
var rk = this.printKDistantfromLeaf(node.right, k);
var isLeaf = lk == -1 && lk == rk;
if (lk == 0 || rk == 0 || (isLeaf && k == 0))
document.write(" " + node.data);
// Leaf node
if (isLeaf && k > 0)
return k - 1;
// Parent of left leaf
if (lk > 0 && lk < k)
return lk - 1;
// Parent of right leaf
if (rk > 0 && rk < k)
return rk - 1;
return -2;
}
}
// Driver code
var tree = new BinaryTree();
// Let us construct the tree shown
// in above diagram
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
document.write("Nodes at distance 2 are :<br>");
tree.printKDistantfromLeaf(tree.root, 2);
// This code is contributed by rdtank
</script>
Nodes at distance 2 are : 3 1
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Otro enfoque :
C++
// Print all nodes that are at distance k from a leaf node
#include <iostream>
using namespace std;
struct bstnode {
int data;
bstnode* right;
bstnode* left;
};
bstnode* newnode(int data)
{
bstnode* temp = new bstnode();
temp->data = data;
temp->right = temp->left = NULL;
return temp;
}
void del(bstnode* root)
{
if (root != NULL) {
del(root->left);
del(root->right);
delete root;
}
}
int printk(bstnode* root, int k)
{
if (root == NULL)
return 0;
int l = printk(root->left, k);
int r = printk(root->right, k);
if (l == k || r == k)
cout << root->data << " ";
return 1 + max(l, r);
}
int main()
{
bstnode* root = NULL;
root = newnode(1);
root->left = newnode(2);
root->right = newnode(3);
root->left->left = newnode(4);
root->left->right = newnode(5);
root->right->left = newnode(6);
root->right->right = newnode(7);
root->right->left->right = newnode(8);
// root->right->right->right=newnode(9);
int k = 2;
printk(root, k);
del(root);
return 0;
// This approach is given by gourabn2000
}
3 1
Complejidad de tiempo: O (n) ya que el código hace un recorrido de árbol simple.
Espacio auxiliar : O(h) como pila de llamadas de función se usa donde h=altura del árbol.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA