Dado un árbol binario, imprímalo verticalmente. El siguiente ejemplo ilustra el recorrido de orden vertical.
1
/ \
2 3
/ \ / \
4 5 6 7
/ \
8 9
The output of print this tree vertically will be:
4
2
1 5 6
3 8
7
9
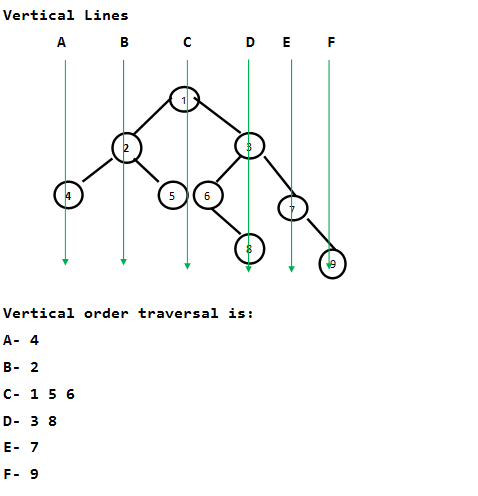
Hemos discutido una solución O(n 2 ) en la publicación anterior . En esta publicación, se analiza una solución eficiente basada en el mapa hash. Necesitamos verificar las distancias horizontales desde la raíz para todos los Nodes. Si dos Nodes tienen la misma Distancia Horizontal (HD), entonces están en la misma línea vertical. La idea de HD es simple. HD para raíz es 0, un borde derecho (borde que se conecta al subárbol derecho) se considera como una distancia horizontal de +1 y un borde izquierdo se considera como una distancia horizontal de -1. Por ejemplo, en el árbol anterior, HD para el Node 4 está en -2, HD para el Node 2 es -1, HD para 5 y 6 es 0 y HD para el Node 7 es +2.
Podemos hacer un recorrido de preorden del árbol binario dado. Mientras recorremos el árbol, podemos calcular HD de forma recursiva. Inicialmente pasamos la distancia horizontal como 0 para la raíz. Para el subárbol izquierdo, pasamos la Distancia horizontal como Distancia horizontal de la raíz menos 1. Para el subárbol derecho, pasamos la Distancia horizontal como Distancia horizontal de la raíz más 1. Para cada valor HD, mantenemos una lista de Nodes en un mapa hash. Cada vez que vemos un Node en el recorrido, vamos a la entrada del mapa hash y agregamos el Node al mapa hash usando HD como clave en un mapa.
A continuación se muestra la implementación en C++ del método anterior. Gracias a Chirag por proporcionar la siguiente implementación de C++.
C++
// C++ program for printing vertical order of a given binary tree
#include <iostream>
#include <vector>
#include <map>
using namespace std;
// Structure for a binary tree node
struct Node
{
int key;
Node *left, *right;
};
// A utility function to create a new node
struct Node* newNode(int key)
{
struct Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return node;
}
// Utility function to store vertical order in map 'm'
// 'hd' is horizontal distance of current node from root.
// 'hd' is initially passed as 0
void getVerticalOrder(Node* root, int hd, map<int, vector<int>> &m)
{
// Base case
if (root == NULL)
return;
// Store current node in map 'm'
m[hd].push_back(root->key);
// Store nodes in left subtree
getVerticalOrder(root->left, hd-1, m);
// Store nodes in right subtree
getVerticalOrder(root->right, hd+1, m);
}
// The main function to print vertical order of a binary tree
// with the given root
void printVerticalOrder(Node* root)
{
// Create a map and store vertical order in map using
// function getVerticalOrder()
map < int,vector<int> > m;
int hd = 0;
getVerticalOrder(root, hd,m);
// Traverse the map and print nodes at every horizontal
// distance (hd)
map< int,vector<int> > :: iterator it;
for (it=m.begin(); it!=m.end(); it++)
{
for (int i=0; i<it->second.size(); ++i)
cout << it->second[i] << " ";
cout << endl;
}
}
// Driver program to test above functions
int main()
{
Node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
root->right->right->right = newNode(9);
cout << "Vertical order traversal is n";
printVerticalOrder(root);
return 0;
}
Java
// Java program for printing vertical order of a given binary tree
import java.util.TreeMap;
import java.util.Vector;
import java.util.Map.Entry;
public class VerticalOrderBtree
{
// Tree node
static class Node
{
int key;
Node left;
Node right;
// Constructor
Node(int data)
{
key = data;
left = null;
right = null;
}
}
// Utility function to store vertical order in map 'm'
// 'hd' is horizontal distance of current node from root.
// 'hd' is initially passed as 0
static void getVerticalOrder(Node root, int hd,
TreeMap<Integer,Vector<Integer>> m)
{
// Base case
if(root == null)
return;
//get the vector list at 'hd'
Vector<Integer> get = m.get(hd);
// Store current node in map 'm'
if(get == null)
{
get = new Vector<>();
get.add(root.key);
}
else
get.add(root.key);
m.put(hd, get);
// Store nodes in left subtree
getVerticalOrder(root.left, hd-1, m);
// Store nodes in right subtree
getVerticalOrder(root.right, hd+1, m);
}
// The main function to print vertical order of a binary tree
// with the given root
static void printVerticalOrder(Node root)
{
// Create a map and store vertical order in map using
// function getVerticalOrder()
TreeMap<Integer,Vector<Integer>> m = new TreeMap<>();
int hd =0;
getVerticalOrder(root,hd,m);
// Traverse the map and print nodes at every horizontal
// distance (hd)
for (Entry<Integer, Vector<Integer>> entry : m.entrySet())
{
System.out.println(entry.getValue());
}
}
// Driver program to test above functions
public static void main(String[] args) {
// TO DO Auto-generated method stub
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
System.out.println("Vertical Order traversal is");
printVerticalOrder(root);
}
}
// This code is contributed by Sumit Ghosh
Python3
# Python program for printing vertical order of a given
# binary tree
# A binary tree node
class Node:
# Constructor to create a new node
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Utility function to store vertical order in map 'm'
# 'hd' is horizontal distance of current node from root
# 'hd' is initially passed as 0
def getVerticalOrder(root, hd, m):
# Base Case
if root is None:
return
# Store current node in map 'm'
try:
m[hd].append(root.key)
except:
m[hd] = [root.key]
# Store nodes in left subtree
getVerticalOrder(root.left, hd-1, m)
# Store nodes in right subtree
getVerticalOrder(root.right, hd+1, m)
# The main function to print vertical order of a binary
#tree ith given root
def printVerticalOrder(root):
# Create a map and store vertical order in map using
# function getVerticalORder()
m = dict()
hd = 0
getVerticalOrder(root, hd, m)
# Traverse the map and print nodes at every horizontal
# distance (hd)
for index, value in enumerate(sorted(m)):
for i in m[value]:
print (i,end=" ")
print()
# Driver program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
root.right.left.right = Node(8)
root.right.right.right = Node(9)
print ("Vertical order traversal is")
printVerticalOrder(root)
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
C#
// C# program for printing vertical order of a given binary tree
using System;
using System.Collections.Generic;
public class VerticalOrderBtree
{
// Tree node
public class Node {
public int key;
public Node left;
public Node right;
// Constructor
public Node(int data) {
key = data;
left = null;
right = null;
}
}
// Utility function to store vertical order in map 'm'
// 'hd' is horizontal distance of current node from root.
// 'hd' is initially passed as 0
static void getVerticalOrder(Node root, int hd,
SortedDictionary<int,
List<int>> m)
{
// Base case
if (root == null)
return;
// get the vector list at 'hd'
List<int> get = new List<int>();//m[hd];
if(m.ContainsKey(hd))
get.AddRange(m[hd]);
// Store current node in map 'm'
if (get == null) {
get = new List<int>();
get.Add(root.key);
} else
get.Add(root.key);
m[hd] = get;
// Store nodes in left subtree
getVerticalOrder(root.left, hd - 1, m);
// Store nodes in right subtree
getVerticalOrder(root.right, hd + 1, m);
}
// The main function to print vertical order of a binary tree
// with the given root
static void printVerticalOrder(Node root)
{
// Create a map and store vertical order in map using
// function getVerticalOrder()
SortedDictionary<int, List<int>> m = new SortedDictionary<int, List<int>>();
int hd = 0;
getVerticalOrder(root, hd, m);
// Traverse the map and print nodes at every horizontal
// distance (hd)
foreach(KeyValuePair<int, List<int>> entry in m)
{
foreach(int v in entry.Value)
Console.Write(v+" ");
Console.WriteLine();
}
}
// Driver program to test above functions
public static void Main(String[] args) {
// TO DO Auto-generated method stub
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
Console.WriteLine("Vertical Order traversal is");
printVerticalOrder(root);
}
}
// This code is contributed by Rajput-Ji
Vertical order traversal is n4 2 1 5 6 3 8 7 9
La complejidad temporal de la solución basada en hash se puede considerar como O(n) bajo el supuesto de que tenemos una buena función hash que permite operaciones de inserción y recuperación en tiempo O(1). En la implementación de C++ anterior, se usa el mapa de STL . El mapa en STL generalmente se implementa utilizando un árbol de búsqueda binaria autoequilibrado donde todas las operaciones toman tiempo O (Inicio de sesión). Por lo tanto, la complejidad temporal de la implementación anterior es O(nLogn).
Tenga en cuenta que es posible que la solución anterior no imprima los Nodes en el mismo orden vertical en el que aparecen en el árbol. Por ejemplo, el programa anterior imprime 12 antes de las 9. Vea esto para una ejecución de muestra.
1
/ \
2 3
/ / \
4 5 6 7
/ \
8 10 9
\
11
\
12
Consulte la publicación a continuación para conocer la solución basada en el recorrido de orden de nivel. La siguiente publicación se asegura de que los Nodes de una línea vertical se impriman en el mismo orden en que aparecen en el árbol.
Imprima un árbol binario en orden vertical | Conjunto 3 (usando el recorrido de orden de nivel)
Usando el enfoque transversal de pedido anticipado, mantenga el orden de los Nodes en el mismo orden vertical que aparecen en el árbol:
También podemos mantener el orden de los Nodes en el mismo orden vertical en el que aparecen en el árbol. Los Nodes que tengan la misma distancia horizontal se imprimirán según el orden de nivel.
Por ejemplo, en el siguiente diagrama 9 y 12 tienen la misma distancia horizontal. Podemos asegurarnos de que si un Node como 12 viene debajo en la misma línea vertical, se imprime después de un Node como 9
Idea: En lugar de usar la distancia horizontal como clave en el mapa, usaremos la distancia horizontal + la distancia vertical como clave. Sabemos que el número de Nodes no puede ser mayor que el rango de enteros en un árbol binario.
Usaremos los primeros 30 bits de la clave para la distancia horizontal [MSB a LSB] y usaremos los siguientes 30 bits para la distancia vertical. Por lo tanto, las claves se almacenarán en el mapa según nuestros requisitos.
A continuación se muestra la implementación del enfoque anterior.
C++14
// C++ program for printing
// vertical order of a given binary
// tree
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
struct Node* newNode(int data)
{
struct Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
// Store vertical order
// in map "m", hd = horizontal
// distance, vd = vertical distance
void preOrderTraversal(Node* root,
long long int hd,
long long int vd,
map<long long int,
vector<int> >& m)
{
if (!root)
return;
// key = horizontal
// distance (30 bits) + vertical
// distance (30 bits) map
// will store key in sorted
// order. Thus nodes having same
// horizontal distance
// will sort according to
// vertical distance.
long long val = hd << 30 | vd;
// insert in map
m[val].push_back(root->data);
preOrderTraversal(root->left, hd - 1, vd + 1, m);
preOrderTraversal(root->right, hd + 1, vd + 1, m);
}
void verticalOrder(Node* root)
{
// map to store all nodes in vertical order.
// keys will be horizontal + vertical distance.
map<long long int, vector<int> > mp;
preOrderTraversal(root, 0, 1, mp);
// print map
int prekey = INT_MAX;
map<long long int, vector<int> >::iterator it;
for (it = mp.begin(); it != mp.end(); it++) {
if (prekey != INT_MAX
&& (it->first >> 30) != prekey) {
cout << endl;
}
prekey = it->first >> 30;
for (int j = 0; j < it->second.size(); j++)
cout << it->second[j] << " ";
}
}
// Driver code
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
root->right->right->right = newNode(9);
cout << "Vertical order traversal :- " << endl;
verticalOrder(root);
return 0;
}
Java
// Java program for printing vertical order of a given
// binary tree
import java.util.Map.Entry;
import java.util.TreeMap;
import java.util.Vector;
public class VerticalOrderBtree {
// Tree node
static class Node {
int data;
Node left;
Node right;
// Constructor
Node(int key)
{
data = key;
left = null;
right = null;
}
}
// Store vertical order
// in map "m", hd = horizontal
// distance, vd = vertical distance
static void
preOrderTraversal(Node root, long hd, long vd,
TreeMap<Long, Vector<Integer> > m)
{
if (root == null)
return;
// key = horizontal
// distance (30 bits) + vertical
// distance (30 bits) map
// will store key in sorted
// order. Thus nodes having same
// horizontal distance
// will sort according to
// vertical distance.
long val = hd << 30 | vd;
// insert in map
if (m.get(val) != null)
m.get(val).add(root.data);
else {
Vector<Integer> v = new Vector<Integer>();
v.add(root.data);
m.put(val, v);
}
preOrderTraversal(root.left, hd - 1, vd + 1, m);
preOrderTraversal(root.right, hd + 1, vd + 1, m);
}
static void verticalOrder(Node root)
{
// map to store all nodes in vertical order.
// keys will be horizontal + vertical distance.
TreeMap<Long, Vector<Integer> > mp
= new TreeMap<>();
preOrderTraversal(root, 0, 1, mp);
// print map
int prekey = Integer.MAX_VALUE;
for (Entry<Long, Vector<Integer> > entry :
mp.entrySet()) {
if (prekey != Integer.MAX_VALUE
&& (entry.getKey() >> 30) != prekey) {
System.out.println();
}
prekey = (int)(entry.getKey() >> 30);
for (int x : entry.getValue())
System.out.print(x + " ");
}
}
// Driver program to test above functions
public static void main(String[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
System.out.println("Vertical Order traversal :- ");
verticalOrder(root);
}
}
// This code is contributed by Abhijeet Kumar(abhijeet19403)
Python3
import sys
# Python program for printing
# vertical order of a given binary
# tree
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
# Store vertical order
# in map "m", hd = horizontal
# distance, vd = vertical distance
def preOrderTraversal(root, hd, vd, m):
if not root:
return
# key = horizontal
# distance (30 bits) + vertical
# distance (30 bits) map
# will store key in sorted
# order. Thus nodes having same
# horizontal distance
# will sort according to
# vertical distance.
val = hd << 30 | vd
# insert in map
if val in m:
m[val].append(root.data)
else:
m[val] = [root.data]
preOrderTraversal(root.left, hd-1, vd+1, m)
preOrderTraversal(root.right, hd+1, vd+1, m)
def verticalOrder(root):
mp = dict()
preOrderTraversal(root, 0, 0, mp)
# print dictionary
prekey = sys.maxsize
for i in sorted(mp.keys()):
if (prekey != sys.maxsize) and (i >> 30 != prekey):
print()
prekey = i >> 30
for j in mp[i]:
print(j, end=" ")
# Driver code
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
root.right.left.right = Node(8)
root.right.right.right = Node(9)
print("Vertical order traversal :- ")
verticalOrder(root)
# This code is contributed by prashantchandelme.
C#
// C# program for printing vertical order of a given binary
// tree
using System;
using System.Collections.Generic;
public class VerticalOrderBtree {
// Tree node
public class Node {
public int data;
public Node left;
public Node right;
// Constructor
public Node(int val)
{
data = val;
left = null;
right = null;
}
}
// Store vertical order
// in map "m", hd = horizontal
// distance, vd = vertical distance
static void
preOrderTraversal(Node root, long hd, long vd,
SortedDictionary<long, List<int> > m)
{
if (root == null)
return;
// key = horizontal
// distance (30 bits) + vertical
// distance (30 bits) map
// will store key in sorted
// order. Thus nodes having same
// horizontal distance
// will sort according to
// vertical distance.
long val = hd << 30 | vd;
// insert in map
if (m.ContainsKey(val) == true)
m[val].Add(root.data);
else {
List<int> v = new List<int>();
v.Add(root.data);
m.Add(val, v);
}
preOrderTraversal(root.left, hd - 1, vd + 1, m);
preOrderTraversal(root.right, hd + 1, vd + 1, m);
}
static void verticalOrder(Node root)
{
// map to store all nodes in vertical order.
// keys will be horizontal + vertical distance.
SortedDictionary<long, List<int> > mp
= new SortedDictionary<long, List<int> >();
preOrderTraversal(root, 0, 1, mp);
// print map
int prekey = Int32.MaxValue;
foreach(KeyValuePair<long, List<int> > entry in mp)
{
if (prekey != Int32.MaxValue
&& (entry.Key >> 30) != prekey) {
Console.WriteLine();
}
prekey = (int)entry.Key >> 30;
foreach(int v in entry.Value)
Console.Write(v + " ");
}
}
// Driver program to test above functions
public static void Main(String[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.left = new Node(6);
root.right.right = new Node(7);
root.right.left.right = new Node(8);
root.right.right.right = new Node(9);
Console.WriteLine("Vertical Order traversal :- ");
verticalOrder(root);
}
}
// This code is contributed by Abhijeet Kumar(abhijeet19403)
Vertical order traversal :- 4 2 1 5 6 3 8 7 9
Complejidad Temporal: O(n Log n).
Espacio Auxiliar: O(n)
Otro enfoque que utiliza el método computeIfAbsent:
Podemos escribir el código de una manera más concisa, usando el método computeIfAbsent del mapa en Java y usando un mapa de árbol para la clasificación natural basada en claves.
A continuación se muestra la implementación del enfoque anterior.
Java
// Java Program for above approach
import java.util.ArrayList;
import java.util.List;
import java.util.Map;
import java.util.TreeMap;
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree {
Node root;
// Values class
class Values {
int max, min;
}
// Program to find vertical Order
public void verticalOrder(Node node)
{
Values val = new Values();
// Create TreeMap
Map<Integer, List<Integer> > map
= new TreeMap<Integer, List<Integer> >();
// Function Call to findHorizontalDistance
findHorizontalDistance(node, val, val, 0, map);
// Iterate over map.values()
for (List<Integer> list : map.values()) {
System.out.println(list);
}
// Print "done"
System.out.println("done");
}
// Program to find Horizontal Distance
public void findHorizontalDistance(
Node node, Values min, Values max, int hd,
Map<Integer, List<Integer> > map)
{
// If node is null
if (node == null)
return;
// if hd is less than min.min
if (hd < min.min)
min.min = hd;
// if hd is greater than min.min
if (hd > max.max)
max.max = hd;
// Using computeIfAbsent
map.computeIfAbsent(hd,
k -> new ArrayList<Integer>())
.add(node.data);
// Function Call with hd equal to hd - 1
findHorizontalDistance(node.left, min, max, hd - 1,
map);
// Function Call with hd equal to hd + 1
findHorizontalDistance(node.right, min, max,
hd + 1, map);
}
// Driver Code
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
/* Let us construct the tree shown
in above diagram */
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.root.right.left.right = new Node(8);
tree.root.right.right.right = new Node(9);
System.out.println("vertical order traversal is :");
// Function Call
tree.verticalOrder(tree.root);
}
}
vertical order traversal is : [4] [2] [1, 5, 6] [3, 8] [7] [9] done
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Otro enfoque utilizando el método de mapa desordenado:
Hemos visto el mapa ordenado arriba, pero su complejidad es O (n logn), y tampoco imprime los Nodes verticales de la misma distancia horizontal en el orden correcto.
aquí implementamos esto usando un mapa desordenado, ya que el mapa desordenado se implementa usando una tabla hash, su complejidad es O (n), mejor que usar un mapa ordenado que se implementa usando un BST.
aquí, para imprimir todos los Nodes de la misma distancia horizontal desde la raíz, usamos mn y mx, dos variables que almacenan la distancia horizontal mínima y máxima desde la raíz.
C++
// C++ program for printing vertical
// order of a given binary tree using BFS
#include <bits/stdc++.h>
using namespace std;
// Structure for a binary tree node
struct Node {
int key;
Node *left, *right;
};
// A function to create a new node
Node* newNode(int key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return node;
}
// The main function to print vertical
// order of a binary tree with given root
void printVerticalOrder(Node* root)
{
// Base case
if (!root) return;
// Create a map and store vertical
// order in map using
// function getVerticalOrder()
unordered_map<int, vector<int> > m;
int hd = 0;
// Create queue to do level order
// traversal Every item of queue contains
// node and horizontal distance
queue<pair<Node*, int> > q;
q.push({root, hd});
// mn and mx contain the minimum and
// maximum horizontal distance from root
int mn=0,mx=0;
while (q.size()>0) {
// pop from queue front
pair<Node*, int> temp = q.front();
q.pop();
hd = temp.second;
Node* node = temp.first;
// insert this node's data
// in vector of hash
m[hd].push_back(node->key);
if (node->left)
q.push({node->left, hd - 1});
if (node->right)
q.push({node->right, hd + 1});
// Update mn and mx
if(mn>hd)
mn=hd;
else if(mx<hd)
mx=hd;
}
// run the loop from minimum to maximum
// every horizontal distance hd
for (int i=mn;i<=mx;i++)
{
vector<int> tmp=m[i];
for(int j=0;j<tmp.size();j++)
cout<<tmp[j]<<" ";
cout<<endl;
}
}
// Driver program to test above functions
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
root->right->right->right = newNode(9);
root->right->right->left = newNode(10);
root->right->right->left->right = newNode(11);
root->right->right->left->right->right = newNode(12);
cout << "Vertical order traversal is \n";
printVerticalOrder(root);
return 0;
}
Vertical order traversal is 4 2 1 5 6 3 8 10 7 11 9 12
Complejidad temporal: O(n)
Complejidad espacial: O(n)
Aquí todos los Nodes de la misma distancia horizontal se imprimirán en el orden correcto, es decir, de arriba a abajo.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA