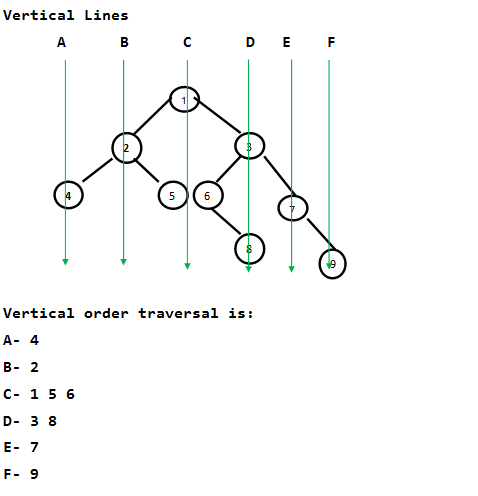
Dado un árbol binario, imprímalo verticalmente. El siguiente ejemplo ilustra el recorrido de orden vertical.
1
/ \
2 3
/ \ / \
4 5 6 7
\ \
8 9
The output of print this tree vertically will be:
4
2
1 5 6
3 8
7
9
Hemos discutido un enfoque eficiente en la publicación a continuación.
Imprima un árbol binario en orden vertical | Conjunto 2 (Método basado en Hashmap)
La solución anterior utiliza un recorrido de preorden y Hashmap para almacenar Nodes de acuerdo con las distancias horizontales. Dado que el enfoque anterior utiliza un recorrido de orden previo, es posible que los Nodes en una línea vertical no se impriman en el mismo orden en que aparecen en el árbol. Por ejemplo, la solución anterior imprime 12 antes de las 9 en el árbol de abajo. Vea esto para una ejecución de muestra.
1
/ \
2 3
/ \ / \
4 5 6 7
\ / \
8 10 9
\
11
\
12
Si usamos el recorrido por orden de nivel , podemos asegurarnos de que si un Node como el 12 viene debajo en la misma línea vertical, se imprime después de un Node como el 9 que viene arriba en la línea vertical.
1. To maintain a hash for the branch of each node.
2. Traverse the tree in level order fashion.
3. In level order traversal, maintain a queue
which holds, node and its vertical branch.
* pop from queue.
* add this node's data in vector corresponding
to its branch in the hash.
* if this node hash left child, insert in the
queue, left with branch - 1.
* if this node hash right child, insert in the
queue, right with branch + 1.
Implementación:
C++
// C++ program for printing vertical order
// of a given binary tree using BFS.
#include <bits/stdc++.h>
using namespace std;
// Structure for a binary tree node
struct Node {
int key;
Node *left, *right;
};
// A utility function to create a new node
Node* newNode(int key)
{
Node* node = new Node;
node->key = key;
node->left = node->right = NULL;
return node;
}
// The main function to print vertical order of a
// binary tree with given root
void printVerticalOrder(Node* root)
{
// Base case
if (!root)
return;
// Create a map and store vertical order in
// map using function getVerticalOrder()
map<int, vector<int> > m;
int hd = 0;
// Create queue to do level order traversal.
// Every item of queue contains node and
// horizontal distance.
queue<pair<Node*, int> > que;
que.push(make_pair(root, hd));
while (!que.empty()) {
// pop from queue front
pair<Node*, int> temp = que.front();
que.pop();
hd = temp.second;
Node* node = temp.first;
// insert this node's data in vector of hash
m[hd].push_back(node->key);
if (node->left != NULL)
que.push(make_pair(node->left, hd - 1));
if (node->right != NULL)
que.push(make_pair(node->right, hd + 1));
}
// Traverse the map and print nodes at
// every horizontal distance (hd)
map<int, vector<int> >::iterator it;
for (it = m.begin(); it != m.end(); it++) {
for (int i = 0; i < it->second.size(); ++i)
cout << it->second[i] << " ";
cout << endl;
}
}
// Driver program to test above functions
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->right->left->right = newNode(8);
root->right->right->right = newNode(9);
root->right->right->left = newNode(10);
root->right->right->left->right = newNode(11);
root->right->right->left->right->right = newNode(12);
cout << "Vertical order traversal is \n";
printVerticalOrder(root);
return 0;
}
Java
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Map;
import java.util.Queue;
import java.util.TreeMap;
class Node {
int key;
Node left, right;
// A utility function to create a new node
Node newNode(int key)
{
Node node = new Node();
node.key = key;
node.left = node.right = null;
return node;
}
}
class Qobj {
int hd;
Node node;
Qobj(int hd, Node node)
{
this.hd = hd;
this.node = node;
}
}
public class VerticalOrderTraversal {
// The main function to print vertical order of a
// binary tree with given root
static void printVerticalOrder(Node root)
{
// Base case
if (root == null)
return;
// Create a map and store vertical order in
// map using function getVerticalOrder()
TreeMap<Integer, ArrayList<Integer> > m = new TreeMap<>();
int hd = 0;
// Create queue to do level order traversal.
// Every item of queue contains node and
// horizontal distance.
Queue<Qobj> que = new LinkedList<Qobj>();
que.add(new Qobj(0, root));
while (!que.isEmpty()) {
// pop from queue front
Qobj temp = que.poll();
hd = temp.hd;
Node node = temp.node;
// insert this node's data in array of hash
if (m.containsKey(hd)) {
m.get(hd).add(node.key);
}
else {
ArrayList<Integer> al = new ArrayList<>();
al.add(node.key);
m.put(hd, al);
}
if (node.left != null)
que.add(new Qobj(hd - 1, node.left));
if (node.right != null)
que.add(new Qobj(hd + 1, node.right));
}
// Traverse the map and print nodes at
// every horizontal distance (hd)
for (Map.Entry<Integer, ArrayList<Integer> > entry : m.entrySet()) {
ArrayList<Integer> al = entry.getValue();
for (Integer i : al)
System.out.print(i + " ");
System.out.println();
}
}
// Driver program to test above functions
public static void main(String ar[])
{
Node n = new Node();
Node root;
root = n.newNode(1);
root.left = n.newNode(2);
root.right = n.newNode(3);
root.left.left = n.newNode(4);
root.left.right = n.newNode(5);
root.right.left = n.newNode(6);
root.right.right = n.newNode(7);
root.right.left.right = n.newNode(8);
root.right.right.right = n.newNode(9);
root.right.right.left = n.newNode(10);
root.right.right.left.right = n.newNode(11);
root.right.right.left.right.right = n.newNode(12);
System.out.println("Vertical order traversal is ");
printVerticalOrder(root);
}
}
Python3
# python3 Program to print zigzag traversal of binary tree
import collections
# Binary tree node
class Node:
# Constructor to create a new node
def __init__(self, data):
self.data = data
self.left = self.right = None
# function to print vertical order traversal of binary tree
def verticalTraverse(root):
# Base case
if root is None:
return
# Create empty queue for level order traversal
queue = []
# create a map to store nodes at a particular
# horizontal distance
m = {}
# map to store horizontal distance of nodes
hd_node = {}
# enqueue root
queue.append(root)
# store the horizontal distance of root as 0
hd_node[root] = 0
m[0] = [root.data]
# loop will run while queue is not empty
while len(queue) > 0:
# dequeue node from queue
temp = queue.pop(0)
if temp.left:
# Enqueue left child
queue.append(temp.left)
# Store the horizontal distance of left node
# hd(left child) = hd(parent) -1
hd_node[temp.left] = hd_node[temp] - 1
hd = hd_node[temp.left]
if m.get(hd) is None:
m[hd] = []
m[hd].append(temp.left.data)
if temp.right:
# Enqueue right child
queue.append(temp.right)
# store the horizontal distance of right child
# hd(right child) = hd(parent) + 1
hd_node[temp.right] = hd_node[temp] + 1
hd = hd_node[temp.right]
if m.get(hd) is None:
m[hd] = []
m[hd].append(temp.right.data)
# Sort the map according to horizontal distance
sorted_m = collections.OrderedDict(sorted(m.items()))
# Traverse the sorted map and print nodes at each horizontal distance
for i in sorted_m.values():
for j in i:
print(j, " ", end ="")
print()
# Driver program to check above function
"""
Constructed binary tree is
1
/ \
2 3
/ \ / \
4 5 6 7
\ / \
8 10 9
\
11
\
12
"""
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
root.right.left.right = Node(8)
root.right.right.left = Node(10)
root.right.right.right = Node(9)
root.right.right.left.right = Node(11)
root.right.right.left.right.right = Node(12)
print("Vertical order traversal is ")
verticalTraverse(root)
# This code is contributed by Shweta Singh
C#
// C# program to implement the
// above approach
using System;
using System.Collections;
using System.Collections.Generic;
class Node{
public int key;
public Node left, right;
// A utility function to
// create a new node
public Node newNode(int key)
{
Node node = new Node();
node.key = key;
node.left = node.right =
null;
return node;
}
}
class Qobj{
public int hd;
public Node node;
public Qobj(int hd,
Node node)
{
this.hd = hd;
this.node = node;
}
}
class VerticalOrderTraversal{
// The main function to print
// vertical order of a binary
// tree with given root
static void printVerticalOrder(Node root)
{
// Base case
if (root == null)
return;
// Create a map and store vertical
// order in map using function
// getVerticalOrder()
SortedDictionary<int,
ArrayList> m =
new SortedDictionary<int,
ArrayList>();
int hd = 0;
// Create queue to do level order
// traversal. Every item of queue
// contains node and horizontal
// distance.
Queue que = new Queue();
que.Enqueue(new Qobj(0, root));
while(que.Count != 0)
{
// pop from queue front
Qobj temp = (Qobj)que.Dequeue();
hd = temp.hd;
Node node = temp.node;
// insert this node's data in
// array of hash
if (m.ContainsKey(hd))
{
m[hd].Add(node.key);
}
else
{
ArrayList al = new ArrayList();
al.Add(node.key);
m[hd] = al;
}
if (node.left != null)
que.Enqueue(new Qobj(hd - 1,
node.left));
if (node.right != null)
que.Enqueue(new Qobj(hd + 1,
node.right));
}
// Traverse the map and print
// nodes at every horizontal
// distance (hd)
foreach(KeyValuePair<int,
ArrayList> entry in m)
{
ArrayList al = (ArrayList)entry.Value;
foreach (int i in al)
Console.Write(i + " ");
Console.Write("\n");
}
}
// Driver code
public static void Main(string []arr)
{
Node n = new Node();
Node root;
root = n.newNode(1);
root.left = n.newNode(2);
root.right = n.newNode(3);
root.left.left = n.newNode(4);
root.left.right = n.newNode(5);
root.right.left = n.newNode(6);
root.right.right = n.newNode(7);
root.right.left.right = n.newNode(8);
root.right.right.right = n.newNode(9);
root.right.right.left = n.newNode(10);
root.right.right.left.right = n.newNode(11);
root.right.right.left.right.right = n.newNode(12);
Console.Write("Vertical order traversal is \n");
printVerticalOrder(root);
}
}
// This code is contributed by Rutvik_56
Javascript
<script>
// Javascript program to implement the
// above approach
class Node
{
constructor()
{
this.key = 0;
this.left = null;
this.right = null;
}
}
// A utility function to
// create a new node
function newNode(key)
{
var node = new Node();
node.key = key;
node.left = node.right =
null;
return node;
}
class Qobj{
constructor(hd, node)
{
this.hd = hd;
this.node = node;
}
}
// The main function to print
// vertical order of a binary
// tree with given root
function printVerticalOrder(root)
{
// Base case
if (root == null)
return;
// Create a map and store vertical
// order in map using function
// getVerticalOrder()
var m = new Map();
var hd = 0;
// Create queue to do level order
// traversal. Every item of queue
// contains node and horizontal
// distance.
var que = [];
que.push(new Qobj(0, root));
while(que.length != 0)
{
// pop from queue front
var temp = que[0];
que.shift();
hd = temp.hd;
var node = temp.node;
// insert this node's data in
// array of hash
if (m.has(hd))
{
var al = m.get(hd);
al.push(node.key);
m.set(hd, al);
}
else
{
var al = [];
al.push(node.key);
m.set(hd, al);
}
if (node.left != null)
que.push(new Qobj(hd - 1,
node.left));
if (node.right != null)
que.push(new Qobj(hd + 1,
node.right));
}
// Traverse the map and print
// nodes at every horizontal
// distance (hd)
[...m].sort((a,b)=>a[0]-b[0]).forEach(tmp => {
var al = tmp[1];
for(var i of al)
document.write(i + " ");
document.write("<br>");
});
}
// Driver code
var root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(6);
root.right.right = newNode(7);
root.right.left.right = newNode(8);
root.right.right.right = newNode(9);
root.right.right.left = newNode(10);
root.right.right.left.right = newNode(11);
root.right.right.left.right.right = newNode(12);
document.write("Vertical order traversal is <br>");
printVerticalOrder(root);
// This code is contributed by famously.
</script>
Vertical order traversal is 4 2 1 5 6 3 8 10 7 11 9 12
La complejidad temporal de la implementación anterior es O(n Log n). Tenga en cuenta que la implementación anterior utiliza un mapa que se implementa mediante BST de autoequilibrio.
Podemos reducir la complejidad del tiempo a O(n) usando unordered_map. Para imprimir los Nodes en el orden deseado, podemos tener 2 variables que indiquen la distancia horizontal mínima y máxima. Simplemente podemos iterar desde la distancia horizontal mínima a la máxima y obtener los valores correspondientes del Mapa. Entonces es O(n)
Espacio Auxiliar: O(n)
?list=PLqM7alHXFySGwXaessYMemAnITqlZdZVE
Este artículo es una contribución de Sahil Chhabra (akku) . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA