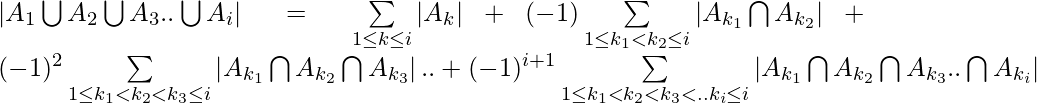En el campo de la combinatoria, es un método de conteo utilizado para calcular la cardinalidad del conjunto de unión. De acuerdo con el principio básico de Inclusión-Exclusión :
- Para 2 conjuntos finitos
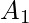 y
y 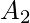 , que son subconjuntos del conjunto Universal, entonces
, que son subconjuntos del conjunto Universal, entonces 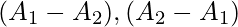 y
y  son conjuntos disjuntos.
son conjuntos disjuntos.
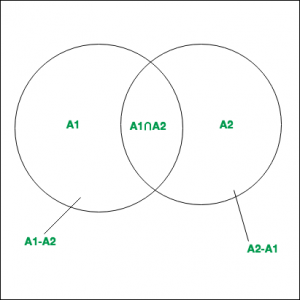
-
De ahí que se pueda decir que,

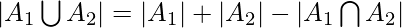 .
. - Análogamente para 3 conjuntos finitos
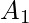 ,
, 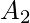 y
y 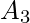 ,
, 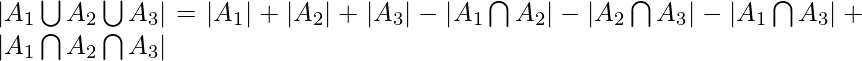
Principio :
El principio de inclusión-exclusión dice que para cualquier número de conjuntos finitos ![]() , la unión de los conjuntos viene dada por = Suma de los tamaños de todos los conjuntos individuales – Suma de todas las intersecciones de 2 conjuntos + Suma de todas las intersecciones de 3 conjuntos – Suma de los 4 -set intersecciones .. +
, la unión de los conjuntos viene dada por = Suma de los tamaños de todos los conjuntos individuales – Suma de todas las intersecciones de 2 conjuntos + Suma de todas las intersecciones de 3 conjuntos – Suma de los 4 -set intersecciones .. + ![]() Suma de todas las intersecciones i-set.
Suma de todas las intersecciones i-set.
En general se puede decir que,
Propiedades :
- Calcula el número total de elementos que satisfacen al menos una de varias propiedades.
- Previene el problema de la doble contabilización.
Ejemplo 1:
Como se muestra en el diagrama, se dan 3 conjuntos finitos A, B y C con sus valores correspondientes. Calcular ![]() _
_
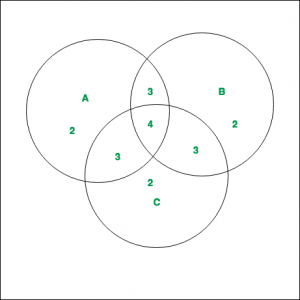
Solución:
los valores de las regiones correspondientes, como se puede observar en el diagrama, son: ![]()
![]()
Aplicando el principio de Inclusión-Exclusión, 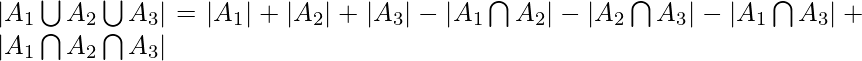
![]()
Aplicaciones:
- Desordenes
Para determinar el número de desarreglos (o permutaciones) de n objetos tales que ningún objeto está en su posición original (como el problema de la verificación del sombrero).
Como ejemplo podemos considerar los desarreglos del número en los siguientes casos:
Para i = 1, el número total de desarreglos es 0.
Para i = 2, el número total de desarreglos es 1. Esto es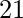 .
.
Para i = 3, el número total de trastornos es 2. Estos son y 3 1 2.
y 3 1 2.
Publicación traducida automáticamente
Artículo escrito por Anand_Shekhar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA