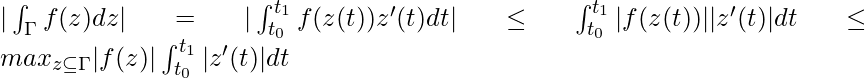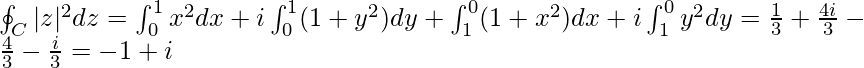Integración compleja – Barcelona Geeks

La integración compleja es una simple extensión de las ideas que desarrollamos en cálculo al mundo complejo. En cálculo real, la diferenciación y la integración son, en términos generales, operaciones inversas (salvo por la interpretación adicional de la derivada como la pendiente de una función y la integral como el área bajo la curva). Veremos que la misma relación inversa entre diferenciación e integración existe en el dominio complejo; pero además, la diferenciación y la integración son también operaciones aproximadamente equivalentes. Pero para ver este sorprendente resultado, tenemos que esperar hasta el Teorema de Cauchy. Este artículo crece sobre los conceptos básicos y es necesario para la preparación para apreciar completamente el Teorema de Cauchy y sus resultados.

Integración compleja de una variable real

Comience con lo básico, es decir, para una función compleja de una variable real, y luego aumente lentamente a casos más complicados, pero emocionantes, de integración compleja. Supongamos que f es una función de valor complejo de una variable real t. Podemos escribir f(t) = u(t) + iv(t), donde u y v ahora son funciones de valor real de una variable real. Por tanto, podemos definir la integral de f(t) en el intervalo [a, b] como

$\int_{a}^{b}f(t)dt=\int_{a}^{b}u(t)dt+i\int_{a}^{b}v(t)dt$ , f(t) is integrable is it is continuous (Flashback to integration in real calculus), and for that matter, if u(t) and v(t) are continuous. We can clearly see that here f(t) is just a linear combination of u(t) and v(t). Hence all theorems and rules we know for real integration flow directly to this case.

Ejemplo 1: Integra f(t) = 2t + it ² . Aquí, u(t) = 2t y v(t) = t ² . Entonces, para 0≤t≤1.

Solución:

$\int_{0}^{1}f(t)dt=\int_{0}^{1}(2t+it^{2})dt=2\int_{0}^{1}tdt+i\int_{0}^{1}t^{2}dt=1+\frac{i}{3}$

Ejemplo 2: Resolver f(t) = ie ^t . Integrandolo de 0 a 2.

Solución:

$\int_{0}^{2}f(t)dt=\int_{0}^{2}ie^{t}dt=i(e^{2}-1)$

Integrales de contorno

Las integrales de contorno son básicamente la integración de la forma, $\int_{z_{0}}^{z_{1}}f(z)dz$

Donde z ₀ y z ₁ son números complejos. Inmediatamente vemos una dificultad. A diferencia del caso de un intervalo [a, b] donde es obvio cómo ir de a a b, aquí tenemos puntos en el plano complejo y hay infinitas formas de ir de un punto a otro ya que el plano complejo es un plano bidimensional. Por lo tanto, la integral anterior es ambigua. Para hacer esta integración, tenemos que definir un camino de z _o a z ₁ . Esto es similar a las integrales de línea de funciones vectoriales en un espacio tridimensional, donde necesitamos una ruta parametrizada específica para calcular la integral.

Definición: Sean z ₀ y z ₁ dos puntos en el plano complejo. Una curva parametrizada que une z ₀ y z ₁ se puede definir mediante una función continua z: [t ₀ , t ₁ ] → C tal que z(t ₀ ) = z ₀ y z(t ₁ ) = z ₁ . Podemos pensar en t aquí como el tiempo. En cualquier instante dado en el tiempo t ₀ ≤ t ≤ t ₁ , la partícula está en el punto z(t) en el plano complejo. Por lo tanto, vemos que una curva que une z ₀ y z ₁ puede definirse mediante una función z(t) mapeando puntos de dominio t, en el intervalo [t ₀, t ₁ ], a los puntos correspondientes z(t) en el plano complejo, tal que z(t ₀ ) = z ₀ y z(t ₁ ) = z ₁ . Como resultado inmediato de esta definición, podemos descomponer z en sus partes real e imaginaria, y esto es equivalente a dos funciones continuas de valor real x(t) y y(t) definidas en el intervalo [t ₀ , t ₁ ] tal que x(t ₀ ) = x ₀ y x(t ₁ ) = x ₁ y de manera similar para y(t): y(t ₀ ) = y ₀ y y(t ₁ ) = y ₁ , donde z ₀ = x ₀+ iy ₀ y z ₁ = x ₁ + iy ₁ . Llamamos suave a la curva si su velocidad dz(t)/dt = z'(t) es una función continua en el intervalo [t ₀ , t ₁ ] que nunca es cero.

Sea Γ una curva suave parametrizada que une z ₀ con z ₁ , y sea f(z) una función de valores complejos que es continua en Γ. Entonces definimos la integral de f a lo largo de Γ por,

$\int_{\Gamma }^{}f(z)dz=\int_{t_{0}}^{t_{1}}f(z(t))z'(t)dt$

La integral compleja también satisface algunas propiedades como la linealidad y el cambio de signo cuando se integra en la dirección inversa. Las pruebas de estas propiedades son fáciles y se pueden hacer fácilmente usando la definición.

Propiedad de linealidad

∫ _Γ (αf(z) + βg(z))dz = α∫ _Γ f(z)dz + β∫ _Γ g (z))dz

Propiedad de inversión de signo

∫ _−Γ f(z)dz = −∫ _Γ f(z)dz

Ejemplo 1: Considere la función f(z) = |z| ² = x ² + y ² integrada a lo largo de la curva parametrizada por z(t) = t + it para 0 ≤ t ≤ 1.

Solución:

Este es el segmento de línea recta que une el origen y el punto 1+ i. Tenemos aquí ̇dz(t)/dt = z'(t) = 1 + i. Asi que,

$\int_{path}^{}f(z)z'(t)dt = \int_{0}^{1}(t^{2}+t^{2})(1+i)dt=2(1+i)\int_{0}^{1}t^{2}dt=\frac{2}{3}(1+i)$

Ejemplo 2: Considere ahora la función f(z) = 1/z integrada a lo largo de la curva suave Γ parametrizada por z(θ) = R e ^{(i θ)} para 0 ≤ θ ≤ 2π, donde R ≠ 0.

Solución:

La curva es un círculo de radio R con centro en el origen. Aquí f(z(θ)) = (1/R) e ^{(−i θ)} y dz(θ)/dθ = z'(θ) = i R e ^{(i θ)} = iz. Entonces tenemos:

$\int_{path}^{}f(z)z'(θ)dθ=\int_{0}^{2\pi }\frac{1}{z}izdθ=i\int_{0}^{2\pi }dθ = 2\pi i$

Tenga en cuenta que el resultado es independiente de R.

Ejemplo 3: Calcular la integral de ln(z) sobre el círculo unitario |z| = 1. Parametrizar z = e ^iθ .

Solución:

Entonces, considerando 0 ≤ θ ≤ 2π. Aquí tomamos |z| = 1 como se especifica. Ahora, dz(θ)/dθ = z'(θ) = ie ^iθ .

$\int_{|z|=1}^{}f(z)z'(\theta )d\theta = \int_{0}^{2\pi }ln(e^{i\theta })ie^{i\theta }d\theta = -\int_{0}^{2\pi }\theta e^{i\theta }d\theta$

Después de hacer la integración por partes, finalmente obtenemos 2πi.

Resultados de la integración de contornos

Resultado 1: Tome f(z) = 1, luego de acuerdo con la definición anterior,

$\int_{\Gamma }^{}f(z)dz=\int_{t_{0}}^{t_{1}}z'(t)dt$

Resultado 2: La longitud de la curva es la integral de contorno del módulo de dz, la función real |dz|. La longitud de la curva Γ es, por tanto,

$\int_{\Gamma }^{}|dz|=\int_{t_{0}}^{t_{1}}|z'(t)|dt=\int_{t_{0}}^{t_{1}}\sqrt{x'(t)^{2}+y'(t)^{2}}dt$

Resultado 3: Estimación del valor máximo de una integral de contorno.

$|\int_{\Gamma }^{}f(z)dz|=|\int_{t_{0}}^{t_{1}}f(z(t))z'(t)dt|\leq \int_{t_{0}}^{t_{1}}|f(z(t))||z'(t)|dt\leq max_{z\subseteq \Gamma }|f(z)| \int_{t_{0}}^{t_{1}}|z'(t)|dt$

Curva suave por partes

Si Γ ₁ es una curva suave que une z ₀ con z ₁ y Γ ₂ es otra curva suave que une z ₁ con z ₂ , entonces podemos hacer una curva Γ, no necesariamente suave, uniendo z ₀ con z ₂ yendo primero a el punto intermedio z ₁ vía Γ ₁ y luego desde allí vía Γ ₂ hasta nuestro destino z ₂ . La curva resultante Γ sigue siendo continua, pero puede que no sea suave, ya que la velocidad no necesita ser continua en el punto intermedio z ₁. Este tipo de curvas se pueden denominar suaves por partes o contornos, como se denominan popularmente en la literatura. Podemos, por lo tanto, construir curvas que no sean suaves pero que puedan estar formadas por un número finito de curvas suaves, llamadas componentes suaves.

Sea Γ un contorno con n componentes suaves {Γ _j } para j = 1, 2, . . . , n. Si f(z) es una función continua en Γ, entonces la integral de contorno de f a lo largo de Γ se define como

$\int_{\Gamma }^{}f(z)dz=\sum_{j=1}^{n}\int_{\Gamma _{j}}^{}f(z)dz =\int_{\Gamma _{1}}^{}f(z)dz+\int_{\Gamma _{2}}^{}f(z)dz+....+\int_{\Gamma _{n}}^{}f(z)dz$

Ejemplo 1: Encuentra el límite superior de la integral I = $\int_{C}^{}\frac{e^{z}}{z^{2}}dz$ , donde C es la línea recta que une los puntos (0,1) y (2,0).

Solución:

La primera tarea es encontrar |f(z)|. Esto es: |f(z)| = $|\frac{e^{^{z}}}{z^{2}}|=\frac{e^{x}}{x^{2}+y^{2}}$

La línea C se muestra aquí. La ecuación de C es 2y + x – 2 = 0.

Aquí, en la línea C, |f(z)| se convierte en una función de una variable. Poniendo y = (2 – x)/2, obtenemos,

$|f(z)| = \frac{e^{x}}{x^{2}+(\frac{2-x}{2})^{2}}$

El valor máximo alcanzado por |f(z)| es e ^4/5 en x = 4/5.

Ahora la longitud del contorno C es básicamente la distancia entre (0,1) y (2,0), es decir, √5.

Usando el Resultado-3, tenemos I ≤ √5e ^4/5

Ejemplo 2: Integra f(z) = |z| ^{2 de} nuevo, pero sobre un contorno suave por partes.

Solución:

Dividir todo el proceso de integración en cuatro partes.

Para OA, dy = 0. Entonces dz = dx. y = 0, entonces |z| ² = x2 ^.

Para AB, dx = 0. Entonces dz = idy. x = 1 entonces |z| ² = 1+y ² .

Para BC, dy = 0, entonces dz = dx. y = 1 entonces |z| ² = x2 +1 ^.

Para CO, dx = 0, entonces dz = idy. x = 0, entonces |z| ² = y ² .

$\oint_{C}^{}|z|^{2}dz=\int_{0}^{1}x^{2}dx+i\int_{0}^{1}(1+y^{2})dy+\int_{1}^{0}(1+x^{2})dx+i\int_{1}^{0}y^{2}dy =\frac{1}{3}+\frac{4i}{3}-\frac{4}{3}-\frac{i}{3}=-1+i$

Teorema de la independencia del camino

En cálculo vectorial, la integral de línea se vuelve independiente de la trayectoria en algunos casos especiales. Esto sucede cuando la función vectorial se puede expresar como el gradiente de una función escalar. Similar es la noción de independencia del camino en la integración compleja. Si tenemos una función cuya antiderivada existe en una región, podemos decir que la integral de la función será independiente del camino de integración. Un dominio es un subconjunto (o una región) de un plano complejo, en el que cada par de puntos se puede conectar a través de un contorno (o una curva suave por partes).

Sea D un dominio y sea f: D → C una función continua compleja definida sobre D. Decimos que f tiene una antiderivada en D si existe alguna función F: D → C tal que,

F'(z) = $\frac{\mathrm{d}F(z) }{\mathrm{d} z}$ = f(z)

Claramente, F es analítica en D. Sea Γ cualquier contorno en D con extremos z ₀ y z ₁ . Si f tiene una antiderivada F en D, la integral de contorno está dada por, ∫ _Γ f(z)dz = F(z ₁ ) − F(z ₀ ). La prueba es sencilla. Comience con la definición y parametrice Γ por z(t) para 0 ≤ t ≤ 1. Entonces,

$\int_{\Gamma }^{}f(z)dz= \int_{0}^{1}F'(z(t))z'(t)dt=\int_{0}^{1}\frac{\mathrm{d} F(z(t))}{\mathrm{d} t} = F(z(1))-F(z(0))=F(z_{1})-F(z_{0})$

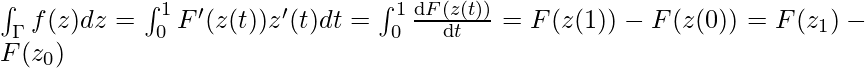
Para un contorno más general, podemos segmentar todo el contorno en componentes suaves individuales {Γj} para j = 1, 2, . . . , n. Entonces, podemos ver fácilmente que los puntos finales de cada componente suave se anulan, dejando atrás los puntos inicial y final.

∫ _Γ f(z)dz = _{j = 1} ∑ ⁿ ∫ _Γj f (z)dz = ∫ _Γ1 f(z)dz + ∫ _Γ2 f(z)dz + …. + ∫ _Γn f(z)dz = F(τ ₁ ) − F(z ₀ ) + F(τ ₂ ) − F(τ ₁ )+….+F(z ₁ ) − F (τ _n−1 ) = F(z ₁ ) − F(z ₀ )

Este resultado dice que si una función f tiene una antiderivada, entonces sus integrales de contorno no dependen de la trayectoria precisa, sino solo de los puntos extremos. Si ahora tenemos un contorno cerrado, lo que significa que los puntos inicial y final coinciden, entonces la integral de contorno cerrado en tal caso es cero. Dicho explícitamente, si Γ es un contorno cerrado en algún dominio D y f : D → C tiene una antiderivada en D, entonces,

$\oint_{\Gamma }^{}f(z)dz=0$

Esta es la declaración matemática precisa de la independencia de la trayectoria de una función compleja, cuya antiderivada existe en el dominio dado. Por ejemplo, los exponenciales complejos y los polinomios son funciones cuya antiderivada existe y, por lo tanto, sus integrales de contorno cerradas son cero según el teorema de independencia de trayectoria.

Publicación traducida automáticamente

Artículo escrito por srimandutta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Integración compleja de una variable real

Integrales de contorno

Deja una respuesta Cancelar la respuesta