Las integrales definidas son la extensión después de las integrales indefinidas, las integrales definidas tienen límites [a, b]. Da el área de una curva delimitada entre límites dados.
![]() , It denotes the area of curve F(x) bounded between a and b, where a is the lower limit and b is the upper limit.
, It denotes the area of curve F(x) bounded between a and b, where a is the lower limit and b is the upper limit.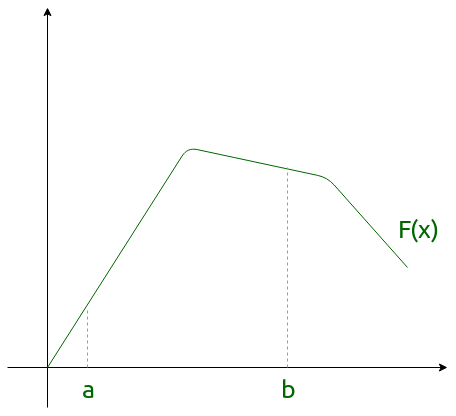
Nota: Si f es una función continua definida en el intervalo cerrado [a, b] y F es una antiderivada de f. Entonces ![]()
Aquí, la función f debe estar bien definida y ser continua en [a, b].
Ejemplo: ![]()
Solución:
![Rendered by QuickLaTeX.com Since, \int x^{2}=\frac{x^{3}}{3} \newline \newline \textup{Then F(x)} =\frac{x^{3}}{3} \newline \newline [F(x)]_{1}^{4}= F(4)-F(1) \newline \newline =[\frac{4^{3}}{3} - \frac{1^{3}}{3}]=\frac{65}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3627c9c053789eee6e71b9eb63beebc9_l3.png)
Propiedades de integrales definidas –
Estas propiedades se pueden usar directamente para encontrar el valor de una integral definida particular y también se pueden intercambiar a otras formas si es necesario.
- Preguntas relacionadas con la puerta:
- Puerta 2014
Publicación traducida automáticamente
Artículo escrito por VaibhavRai3 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA