¿Qué es una estructura de datos de árbol?
Un árbol es una estructura de datos no lineal y jerárquica que consta de una colección de Nodes de modo que cada Node del árbol almacena un valor y una lista de referencias a otros Nodes (los «hijos»).
Esta estructura de datos es un método especializado para organizar y almacenar datos en la computadora para usarlos de manera más efectiva. Consiste en un Node central, Nodes estructurales y subNodes, que están conectados a través de los bordes. También podemos decir que la estructura de datos del árbol tiene raíces, ramas y hojas conectadas entre sí.
Definición recursiva:
Un árbol consta de una raíz y cero o más subárboles T 1 , T 2 , … , T k tales que hay una arista desde la raíz del árbol hasta la raíz de cada subárbol.
¿Por qué Tree se considera una estructura de datos no lineal?
Los datos en un árbol no se almacenan de forma secuencial, es decir, no se almacenan linealmente. En cambio, están organizados en múltiples niveles o podemos decir que es una estructura jerárquica. Por esta razón, el árbol se considera una estructura de datos no lineal.
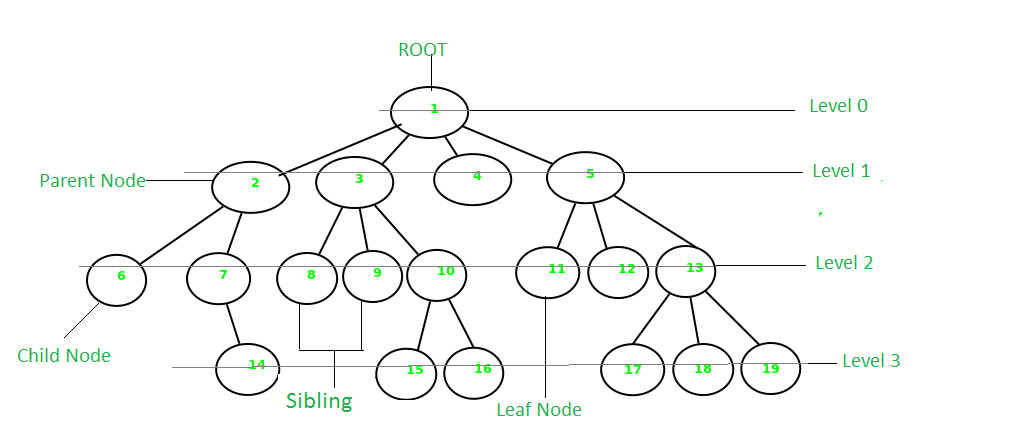
Terminologías básicas en la estructura de datos de árbol:
- Node principal: el Node que es un predecesor de un Node se denomina Node principal de ese Node. { 2} es el Node principal de { 6, 7} .
- Node secundario: el Node que es el sucesor inmediato de un Node se denomina Node secundario de ese Node. Ejemplos: { 6, 7} son los Nodes secundarios de { 2} .
- Node Raíz: El Node más alto de un árbol o el Node que no tiene ningún Node principal se llama Node raíz. { 1} es el Node raíz del árbol. Un árbol no vacío debe contener exactamente un Node raíz y exactamente una ruta desde la raíz a todos los demás Nodes del árbol.
- Node hoja o Node externo: los Nodes que no tienen Nodes secundarios se denominan Nodes hoja. { 6, 14, 8, 9, 15, 16, 4, 11, 12, 17, 18, 19} son los Nodes hoja del árbol.
- Ancestro de un Node: cualquier Node predecesor en la ruta de la raíz a ese Node se denomina Ancestros de ese Node. { 1, 2} son los Nodes antecesores del Node { 7}
- Descendiente: cualquier Node sucesor en la ruta desde el Node hoja hasta ese Node. { 7, 14} son los descendientes del Node. { 2} .
- Hermano: Los hijos del mismo Node padre se llaman hermanos. { 8, 9, 10} se llaman hermanos.
- Nivel de un Node: el recuento de aristas en la ruta desde el Node raíz hasta ese Node. El Node raíz tiene el nivel 0 .
- Node interno: Un Node con al menos un hijo se llama Node interno.
- Vecino de un Node: los Nodes principales o secundarios de ese Node se denominan vecinos de ese Node.
- Subárbol : Cualquier Node del árbol junto con su descendiente.
Propiedades de un árbol:
- Número de aristas: Una arista se puede definir como la conexión entre dos Nodes. Si un árbol tiene N Nodes, tendrá (N-1) aristas. Solo hay un camino desde cada Node a cualquier otro Node del árbol.
- Profundidad de un Node: La profundidad de un Node se define como la longitud del camino desde la raíz hasta ese Node. Cada borde agrega 1 unidad de longitud al camino. Por lo tanto, también se puede definir como el número de aristas en el camino desde la raíz del árbol hasta el Node.
- Altura de un Node: la altura de un Node se puede definir como la longitud del camino más largo desde el Node hasta un Node hoja del árbol.
- Altura del árbol: La altura de un árbol es la longitud del camino más largo desde la raíz del árbol hasta un Node de hoja del árbol.
- Grado de un Node: el recuento total de subárboles adjuntos a ese Node se denomina grado del Node. El grado de un Node hoja debe ser 0 . El grado de un árbol es el grado máximo de un Node entre todos los Nodes del árbol.
Algunas propiedades más son:
- El recorrido en un árbol se realiza mediante el algoritmo de búsqueda primero en profundidad y primero en amplitud.
- No tiene bucle ni circuito.
- No tiene auto-bucle
- Su modelo jerárquico.
Sintaxis:
struct Node
{
datos int;
estructura Node *left_child;
struct Node *right_child;
};
Operación básica del árbol:
Crear: crea un árbol en la estructura de datos.
Insertar: inserta datos en un árbol.
Buscar: busca datos específicos en un árbol para verificar si están presentes o no.
Preorder Traversal: realice el recorrido de un árbol de forma preordenada en la estructura de datos.
Recorrido en orden: realice el desplazamiento de un árbol en orden.
Recorrido posterior a la orden: realiza el desplazamiento de un árbol de manera posterior a la orden.
Ejemplo de estructura de datos de árbol

Aquí,
El Node A es el Node raíz.
B es el padre de D y E
D y E son los hermanos
D, E, F y G son los Nodes hoja
A y B son los ancestros de E
Algunos ejemplos de estructura de datos de árbol: a continuación se describe un código para demostrar algunas de las terminologías anteriores:

C++
// C++ program to demonstrate some of the above
// terminologies
#include <bits/stdc++.h>
using namespace std;
// Function to add an edge between vertices x and y
void addEdge(int x, int y, vector<vector<int> >& adj)
{
adj[x].push_back(y);
adj[y].push_back(x);
}
// Function to print the parent of each node
void printParents(int node, vector<vector<int> >& adj,
int parent)
{
// current node is Root, thus, has no parent
if (parent == 0)
cout << node << "->Root" << endl;
else
cout << node << "->" << parent << endl;
// Using DFS
for (auto cur : adj[node])
if (cur != parent)
printParents(cur, adj, node);
}
// Function to print the children of each node
void printChildren(int Root, vector<vector<int> >& adj)
{
// Queue for the BFS
queue<int> q;
// pushing the root
q.push(Root);
// visit array to keep track of nodes that have been
// visited
int vis[adj.size()] = { 0 };
// BFS
while (!q.empty()) {
int node = q.front();
q.pop();
vis[node] = 1;
cout << node << "-> ";
for (auto cur : adj[node])
if (vis[cur] == 0) {
cout << cur << " ";
q.push(cur);
}
cout << endl;
}
}
// Function to print the leaf nodes
void printLeafNodes(int Root, vector<vector<int> >& adj)
{
// Leaf nodes have only one edge and are not the root
for (int i = 1; i < adj.size(); i++)
if (adj[i].size() == 1 && i != Root)
cout << i << " ";
cout << endl;
}
// Function to print the degrees of each node
void printDegrees(int Root, vector<vector<int> >& adj)
{
for (int i = 1; i < adj.size(); i++) {
cout << i << ": ";
// Root has no parent, thus, its degree is equal to
// the edges it is connected to
if (i == Root)
cout << adj[i].size() << endl;
else
cout << adj[i].size() - 1 << endl;
}
}
// Driver code
int main()
{
// Number of nodes
int N = 7, Root = 1;
// Adjacency list to store the tree
vector<vector<int> > adj(N + 1, vector<int>());
// Creating the tree
addEdge(1, 2, adj);
addEdge(1, 3, adj);
addEdge(1, 4, adj);
addEdge(2, 5, adj);
addEdge(2, 6, adj);
addEdge(4, 7, adj);
// Printing the parents of each node
cout << "The parents of each node are:" << endl;
printParents(Root, adj, 0);
// Printing the children of each node
cout << "The children of each node are:" << endl;
printChildren(Root, adj);
// Printing the leaf nodes in the tree
cout << "The leaf nodes of the tree are:" << endl;
printLeafNodes(Root, adj);
// Printing the degrees of each node
cout << "The degrees of each node are:" << endl;
printDegrees(Root, adj);
return 0;
}
Java
// java code for above approach
import java.io.*;
import java.util.*;
class GFG {
// Function to print the parent of each node
public static void
printParents(int node, Vector<Vector<Integer> > adj,
int parent)
{
// current node is Root, thus, has no parent
if (parent == 0)
System.out.println(node + "->Root");
else
System.out.println(node + "->" + parent);
// Using DFS
for (int i = 0; i < adj.get(node).size(); i++)
if (adj.get(node).get(i) != parent)
printParents(adj.get(node).get(i), adj,
node);
}
// Function to print the children of each node
public static void
printChildren(int Root, Vector<Vector<Integer> > adj)
{
// Queue for the BFS
Queue<Integer> q = new LinkedList<>();
// pushing the root
q.add(Root);
// visit array to keep track of nodes that have been
// visited
int vis[] = new int[adj.size()];
Arrays.fill(vis, 0);
// BFS
while (q.size() != 0) {
int node = q.peek();
q.remove();
vis[node] = 1;
System.out.print(node + "-> ");
for (int i = 0; i < adj.get(node).size(); i++) {
if (vis[adj.get(node).get(i)] == 0) {
System.out.print(adj.get(node).get(i)
+ " ");
q.add(adj.get(node).get(i));
}
}
System.out.println();
}
}
// Function to print the leaf nodes
public static void
printLeafNodes(int Root, Vector<Vector<Integer> > adj)
{
// Leaf nodes have only one edge and are not the
// root
for (int i = 1; i < adj.size(); i++)
if (adj.get(i).size() == 1 && i != Root)
System.out.print(i + " ");
System.out.println();
}
// Function to print the degrees of each node
public static void
printDegrees(int Root, Vector<Vector<Integer> > adj)
{
for (int i = 1; i < adj.size(); i++) {
System.out.print(i + ": ");
// Root has no parent, thus, its degree is
// equal to the edges it is connected to
if (i == Root)
System.out.println(adj.get(i).size());
else
System.out.println(adj.get(i).size() - 1);
}
}
// Driver code
public static void main(String[] args)
{
// Number of nodes
int N = 7, Root = 1;
// Adjacency list to store the tree
Vector<Vector<Integer> > adj
= new Vector<Vector<Integer> >();
for (int i = 0; i < N + 1; i++) {
adj.add(new Vector<Integer>());
}
// Creating the tree
adj.get(1).add(2);
adj.get(2).add(1);
adj.get(1).add(3);
adj.get(3).add(1);
adj.get(1).add(4);
adj.get(4).add(1);
adj.get(2).add(5);
adj.get(5).add(2);
adj.get(2).add(6);
adj.get(6).add(2);
adj.get(4).add(7);
adj.get(7).add(4);
// Printing the parents of each node
System.out.println("The parents of each node are:");
printParents(Root, adj, 0);
// Printing the children of each node
System.out.println(
"The children of each node are:");
printChildren(Root, adj);
// Printing the leaf nodes in the tree
System.out.println(
"The leaf nodes of the tree are:");
printLeafNodes(Root, adj);
// Printing the degrees of each node
System.out.println("The degrees of each node are:");
printDegrees(Root, adj);
}
}
// This code is contributed by rj13to.
Python3
# python program to demonstrate some of the above
# terminologies
# Function to add an edge between vertices x and y
# Function to print the parent of each node
def printParents(node, adj, parent):
# current node is Root, thus, has no parent
if (parent == 0):
print(node, "->Root")
else:
print(node, "->", parent)
# Using DFS
for cur in adj[node]:
if (cur != parent):
printParents(cur, adj, node)
# Function to print the children of each node
def printChildren(Root, adj):
# Queue for the BFS
q = []
# pushing the root
q.append(Root)
# visit array to keep track of nodes that have been
# visited
vis = [0]*len(adj)
# BFS
while (len(q) > 0):
node = q[0]
q.pop(0)
vis[node] = 1
print(node, "-> ", end=" ")
for cur in adj[node]:
if (vis[cur] == 0):
print(cur, " ", end=" ")
q.append(cur)
print("\n")
# Function to print the leaf nodes
def printLeafNodes(Root, adj):
# Leaf nodes have only one edge and are not the root
for i in range(0, len(adj)):
if (len(adj[i]) == 1 and i != Root):
print(i, end=" ")
print("\n")
# Function to print the degrees of each node
def printDegrees(Root, adj):
for i in range(1, len(adj)):
print(i, ": ", end=" ")
# Root has no parent, thus, its degree is equal to
# the edges it is connected to
if (i == Root):
print(len(adj[i]))
else:
print(len(adj[i])-1)
# Driver code
# Number of nodes
N = 7
Root = 1
# Adjacency list to store the tree
adj = []
for i in range(0, N+1):
adj.append([])
# Creating the tree
adj[1].append(2)
adj[2].append(1)
adj[1].append(3)
adj[3].append(1)
adj[1].append(4)
adj[4].append(1)
adj[2].append(5)
adj[5].append(2)
adj[2].append(6)
adj[6].append(2)
adj[4].append(7)
adj[7].append(4)
# Printing the parents of each node
print("The parents of each node are:")
printParents(Root, adj, 0)
# Printing the children of each node
print("The children of each node are:")
printChildren(Root, adj)
# Printing the leaf nodes in the tree
print("The leaf nodes of the tree are:")
printLeafNodes(Root, adj)
# Printing the degrees of each node
print("The degrees of each node are:")
printDegrees(Root, adj)
# This code is contributed by rj13to.
The parents of each node are: 1->Root 2->1 5->2 6->2 3->1 4->1 7->4 The children of each node are: 1-> 2 3 4 2-> 5 6 3-> 4-> 7 5-> 6-> 7-> The leaf nodes of the tree are: 3 5 6 7 The degrees of each node are: 1: 3 2: 2 3: 0 4: 1 5: 0 6: 0 7: 0
Tipos de estructuras de datos de árbol
Los diferentes tipos de estructuras de datos de árbol son los siguientes:
1. Árbol general
Una estructura de datos de árbol general no tiene restricciones en el número de Nodes. Significa que un Node principal puede tener cualquier número de Nodes secundarios.
2. Árbol binario
Un Node de un árbol binario puede tener un máximo de dos Nodes secundarios. En el diagrama de árbol dado, los Nodes B, D y F son los hijos de la izquierda, mientras que E, C y G son los hijos de la derecha.
3. Árbol equilibrado
Si la altura del subárbol izquierdo y el subárbol derecho es igual o difiere como máximo en 1, el árbol se conoce como un árbol equilibrado.

Árbol Equilibrado Árbol Desequilibrado
4. Árbol de búsqueda binario
Como su nombre lo indica, los árboles de búsqueda binarios se utilizan para varios algoritmos de búsqueda y clasificación. Los ejemplos incluyen el árbol AVL y el árbol rojo-negro. Es una estructura de datos no lineal. Muestra que el valor del Node izquierdo es menor que su padre, mientras que el valor del Node derecho es mayor que su padre.
Aplicaciones de la estructura de datos de árbol:
Las aplicaciones de las estructuras de datos de árbol son las siguientes:
1. Árboles de expansión: Es el árbol de ruta más corto utilizado en los enrutadores para dirigir los paquetes al destino.
2. Árbol de búsqueda binaria: es un tipo de estructura de datos de árbol que ayuda a mantener un flujo de datos ordenado.
- Árbol binario completo
- Árbol binario completo
- Árbol binario sesgado
- Árbol binario pegajoso
- Árbol binario extendido
3. Almacenamiento de datos jerárquicos: las estructuras de datos de árbol se utilizan para almacenar los datos jerárquicos, lo que significa que los datos se organizan en forma de orden.
4. Árbol sintáctico: El árbol sintáctico representa la estructura del código fuente del programa, que se utiliza en los compiladores.
5. Trie: es una forma rápida y eficiente de revisión ortográfica dinámica. También se utiliza para ubicar claves específicas dentro de un conjunto.
6. Montón: también es una estructura de datos de árbol que se puede representar en forma de array. Se utiliza para implementar colas de prioridad.