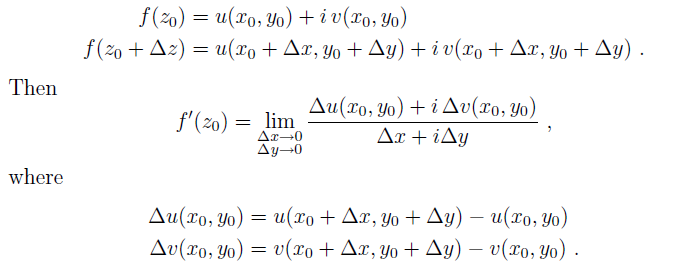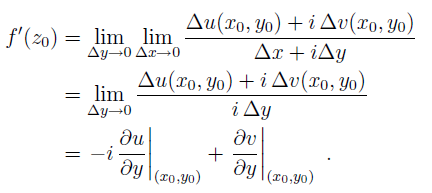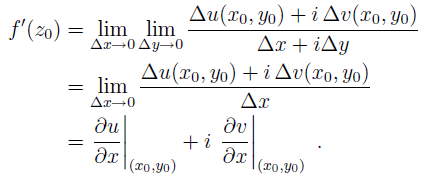Introducción al análisis complejo

El análisis complejo es una rama de las matemáticas que se ocupa de los números complejos, sus funciones y su cálculo. En términos simples, el análisis complejo es una extensión del cálculo de números reales al dominio complejo. Extenderemos las nociones de continuidad, derivadas e integrales, familiares del cálculo, al caso de funciones complejas de una variable compleja. Al hacerlo, nos encontraremos con funciones analíticas, que forman la pieza central de esta introducción. De hecho, en gran medida el análisis complejo es el estudio de funciones analíticas.

El ingrediente básico del análisis complejo es una función analítica, o eso lo conocemos tan bien en cálculo como una función diferenciable. Cualquier número complejo z se puede considerar como un punto en un plano ( x,y ), por lo que z = x+iy, donde i=√-1. De manera similar, cualquier función compleja de una variable compleja z se puede separar en dos funciones, como en   f(z)=u(z)+iv(z), o f(x,y)=u(x ,y)+iv(x,y). Claramente, tales funciones dependen de dos variables independientes y tienen dos funciones separables, por lo que trazar la función necesitaría un espacio de cuatro dimensiones, lo cual es difícil de imaginar.

Por supuesto, el primer punto de partida del cálculo de funciones complejas es comenzar con la continuidad de la función y luego pasar lentamente a la diferenciabilidad en el dominio complejo. 

Continuidad 

Comenzamos con un caso bastante trivial de una función de valor complejo. Supongamos que f es una función de valor complejo de una variable real. Eso significa que si x es un número real, f(x) es un número complejo, que se puede descomponer en sus partes real e imaginaria:   f(x) = u(x)+iv(x) , donde u y v son funciones de valor real de una variable real; es decir, los objetos con los que está familiarizado a partir del cálculo real. Decimos que f es continua en x ₀ si u y v son continuas en x ₀ .

La continuidad de una función de valor complejo de una variable compleja es una propiedad no trivial. Se dice que una función es continua en un punto z _o si tiende al valor f(z _o ) cuando z tiende a z _o . Dado que z vive en un plano complejo (también conocido como plano de Argand), puede acercarse al punto desde varias direcciones. Por lo tanto, necesitamos refinar nuestra definición para satisfacer las nuevas necesidades. 

Formalmente, decimos que f(z) es continua en z _o si, para cualquier ε>0, existe un δ>0, tal que |f(z)-f(z _o )|<ε para todo |zz _o |<δ. Entonces, siempre que z esté dentro de un disco de radio δ con centro en z _o (llamado el vecindario de z _o ) y la función se acerque al valor de f (z _o ). 

analiticidad 

Una vez que hemos establecido las nociones de continuidad de funciones complejas, podemos sumergirnos en la diferenciación de funciones complejas. Mientras discutimos la diferenciación de funciones complejas, veremos que tales funciones necesitan satisfacer un criterio importante, llamado las ecuaciones de Cauchy-Riemann . Si una analogía ayuda, sabemos que para que la derivada de una función real exista finitamente en un punto dado, la función debe ser continua en el punto. Un criterio similar para las funciones complejas son las ecuaciones de Cauchy-Riemann. Pronto veremos la prueba en la siguiente discusión. 

Una función de valor complejo de una variable real se puede diferenciar fácilmente, como f'(x)=u'(x)+iv'(x), donde f(x) es la función de valor complejo de una variable real x. En otras palabras, extendemos la operación de diferenciación linealmente compleja. No hay nada novedoso aquí.

Sin embargo, la situación cambia cuando f se convierte en una función de una variable compleja z . Sabemos que una variable compleja z en sí misma es en realidad un par de dos variables reales x e y . Representamos z como un punto en el plano complejo con un par ordenado ( x,y ) y denotamos z=x+iy. Entonces, esto trae una pregunta sobre cómo diferenciar una función de valor complejo de una variable compleja. Como era de esperar, tenemos una definición de derivada similar al cálculo real:

Entonces, el primer desafío es cómo hacer que δz sea infinitamente pequeño. En el plano complejo, podemos hacerlo desde múltiples direcciones. Como se desprende de la definición, la derivada de la función no debe cambiar en la forma en que se toma el límite. O bien, obtendremos una nueva derivada cada vez que cambiemos los límites. De hecho, lo que estamos haciendo es investigar cómo cambia la función f(z) cuando tomamos δz⇢0, o en otras palabras, δx⇢0 y δy⇢0. En esencia, nuestra derivada no debe cambiar al cambiar el orden de tomar los límites. Y cambiar el orden de los límites no siempre garantiza el mismo valor (¡todos los matemáticos pueden idear una función que pruebe esta proposición!). Entonces, la diferenciabilidad es una propiedad no trivial en el mundo complejo. 

Ahora, escribamos f(z)=u(z)+iv(z) o, de manera equivalente, f(x,y)=u(x,y)+iv(x,y) . 

A continuación, tomamos primero δx⇢0 y luego δy⇢0. Esto es equivalente a tomar δz⇢0 a lo largo del eje imaginario. 

Ahora, al revés, tomamos primero δy⇢0 y luego δx⇢0. Esto es equivalente a tomar δz⇢0 a lo largo del eje real. 

Las dos expresiones concuerdan si y solo si:

Aquí, tenemos las ecuaciones de Cauchy-Riemann. 

Entonces, para comprobar si una función f(z) es diferenciable en un punto z _o =x _o +iy _o , necesitamos ver si satisfacen las ecuaciones de Cauchy-Riemann. Y luego su derivada viene dada por cualquiera de las expresiones obtenidas para f'(z _o ). 

Se puede observar que la diferenciación en el mundo complejo no es fácil y hay muchas funciones que no son realmente diferenciables, incluso las más simples (intenta diferenciar z*, el complejo conjugado de z). 

Podemos decir que una función es analítica u holomorfa en una vecindad de zo _si es diferenciable en esa vecindad. Una función que es analítica sobre todo el plano complejo se dice entera. 

Es importante darse cuenta de que la analiticidad, a diferencia de la diferenciabilidad, no es una propiedad de una función en un punto, sino en un conjunto abierto de puntos. La razón de esto es poder eliminar de la clase de funciones interesantes, funciones que pueden ser derivables en un punto pero en ningún otro lugar. Si bien esto es una rareza en cálculo, es una ocurrencia muy común para funciones de valores complejos de variables complejas. Por ejemplo, considere la función f(z) = |z| ² . Esta función tiene u(x, y) = x ² + y ² y v(x, y) = 0. Por lo tanto, las ecuaciones de Cauchy-Riemann solo se satisfacen en el origen en el plano complejo.