Finite Automata (FA) es la máquina más simple para reconocer patrones. El autómata finito o máquina de estados finitos es una máquina abstracta que consta de cinco elementos o tuplas. Tiene un conjunto de estados y reglas para pasar de un estado a otro, pero depende del símbolo de entrada aplicado. Básicamente, es un modelo abstracto de una computadora digital. La siguiente figura muestra algunas características esenciales de la automatización general.

La figura anterior muestra las siguientes características de los autómatas:
- Aporte
- Producción
- Estados de autómatas
- relación de estado
- Relación de salida
Un autómata finito consta de lo siguiente:
Q : Finite set of states. Σ : set of Input Symbols. q : Initial state. F : set of Final States. δ : Transition Function.
La especificación formal de la máquina es
{ Q, Σ, q, F, δ }
FA se caracteriza en dos tipos:
1) Autómatas finitos deterministas (DFA) –
DFA consists of 5 tuples {Q, Σ, q, F, δ}.
Q : set of all states.
Σ : set of input symbols. ( Symbols which machine takes as input )
q : Initial state. ( Starting state of a machine )
F : set of final state.
δ : Transition Function, defined as δ : Q X Σ --> Q.
En un DFA, para un carácter de entrada en particular, la máquina pasa a un solo estado. Se define una función de transición en cada estado para cada símbolo de entrada. Además, en DFA no se permite el movimiento nulo (o ε), es decir, DFA no puede cambiar de estado sin ningún carácter de entrada.
Por ejemplo, debajo de DFA con Σ = {0, 1} acepta todas las strings que terminan en 0.

Una cosa importante a tener en cuenta es que puede haber muchos DFA posibles para un patrón . Por lo general, se prefiere un DFA con un número mínimo de estados.
2) Autómatas finitos no deterministas (NFA)
NFA es similar a DFA excepto por las siguientes características adicionales:
- Se permite el movimiento nulo (o ε), es decir, puede avanzar sin leer símbolos.
- Capacidad de transmitir a cualquier número de estados para una entrada en particular.
Sin embargo, estas características anteriores no agregan ningún poder a NFA. Si comparamos ambos en términos de potencia, ambos son equivalentes.
Debido a las características adicionales anteriores, NFA tiene una función de transición diferente, el resto es igual que DFA.
δ: Transition Function δ: Q X (Σ U ε ) --> 2 ^ Q.
Como puede ver, la función de transición es para cualquier entrada, incluido nulo (o ε), NFA puede ir a cualquier número de estados.
Por ejemplo, a continuación se muestra un NFA para el problema anterior.
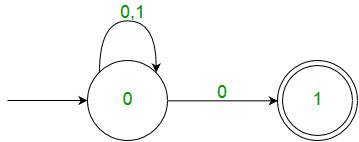
Una cosa importante a tener en cuenta es que, en NFA, si alguna ruta para una string de entrada conduce a un estado final, entonces se acepta la string de entrada . Por ejemplo, en el NFA anterior, hay varias rutas para la string de entrada «00». Dado que uno de los caminos conduce a un estado final, el NFA anterior acepta «00».
Algunos puntos importantes:
- Justificación:
In case of DFA δ : Q X Σ --> Q In case of NFA δ : Q X Σ --> 2Q
Ahora, si observa, descubrirá que QX Σ –> Q es parte de QX Σ –> 2 Q.
En el lado derecho, Q es el subconjunto de 2 Q , lo que indica que Q está contenido en 2 Q o Q es parte de 2 Q , sin embargo, lo contrario no es cierto. Entonces, matemáticamente, podemos concluir que cada DFA es NFA pero no al revés . Sin embargo, hay una manera de convertir un NFA a DFA, por lo que existe un DFA equivalente para cada NFA .
- Tanto NFA como DFA tienen el mismo poder y cada NFA se puede traducir a DFA.
- Puede haber varios estados finales tanto en DFA como en NFA.
- NFA es más un concepto teórico.
- DFA se utiliza en análisis léxico en Compiler.
Consulte el cuestionario sobre expresiones regulares y autómatas finitos .
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA