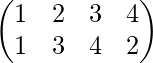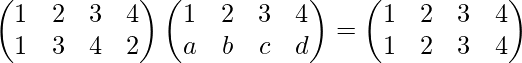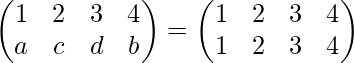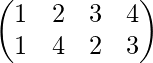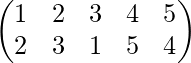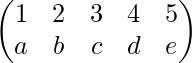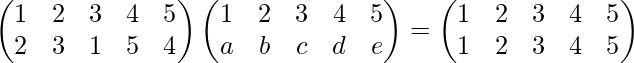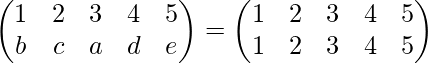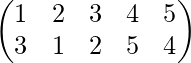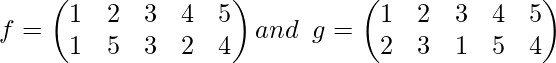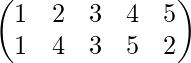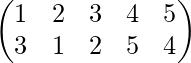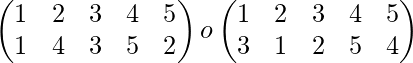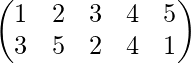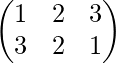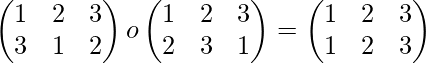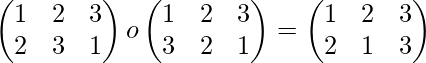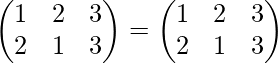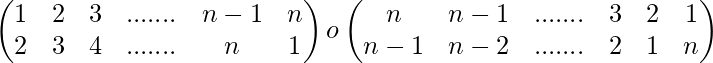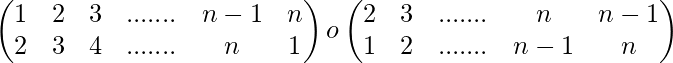Grupo de permutación inversa

Inverso del grupo de permutaciones: si el producto de dos permutaciones es la permutación idéntica, cada una de ellas se denomina inversa entre sí.

Por ejemplo-: Las permutaciones

$\begin{pmatrix} a1 &a2&a3&........&an\\ b1 & b2 & b3&........&bn \end{pmatrix} and \begin{pmatrix} b1 & b2 & b3&........&bn\\ a1 &a2&a3&........&an \end{pmatrix}$

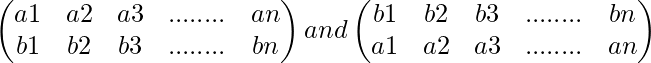
son inversas entre sí ya que su producto es 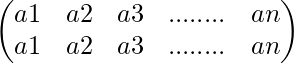$\begin{pmatrix} a1&a2&a3&........&an\\ a1&a2&a3&........&an \end{pmatrix}$

que es una permutación idéntica.

Ejemplo 1-: Encuentra el inverso de la permutación $\begin{pmatrix} 1 & 2 & 3&4\\ 1 & 3 & 4&2 \end{pmatrix}$

Solución-: Sea el inverso de la permutación $\begin{pmatrix} 1 & 2 & 3&4\\ a & b & c&d \end{pmatrix}$ \

donde se van a calcular a, b, c y d.

Entonces, de acuerdo con la definición de inversa de permutación

$\begin{pmatrix} 1 & 2 & 3&4\\ 1 & 3 & 4&2 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3&4\\ a & b & c&d \end{pmatrix}= \begin{pmatrix} 1 & 2 & 3&4\\ 1 & 2 & 3&4 \end{pmatrix}$

o $\begin{pmatrix} 1 & 2 & 3&4\\ a & c & d&b \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3&4\\ 1 & 2 & 3&4 \end{pmatrix}$

∴ segundo=4, c=2, a=1, re=3

∴ El inverso requerido es $\begin{pmatrix} 1 & 2 & 3&4\\ 1 & 4 & 2&3 \end{pmatrix}$

Ejemplo 2-: Calcular A ^-1 si A= $\begin{pmatrix} 1 & 2 & 3&4&5\\ 2&3&1&5&4 \end{pmatrix}$

Solución-: Sea el inverso de A $\begin{pmatrix} 1 & 2 & 3&4&5\\ a&b&c&d&e \end{pmatrix}$

donde se van a calcular a, b, c, d y e.

Entonces, de acuerdo con la definición de inversa de permutación

$\begin{pmatrix} 1 & 2 & 3&4&5\\ 2&3&1&5&4 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3&4&5\\ a&b&c&d&e \end{pmatrix} =\begin{pmatrix} 1 & 2 & 3&4&5\\ 1&2&3&4&5 \end{pmatrix}$

o $\begin{pmatrix} 1 & 2 & 3&4&5\\ b&c&a&d&e \end{pmatrix}= \begin{pmatrix} 1 & 2 & 3&4&5\\ 1&2&3&4&5 \end{pmatrix}$

∴ segundo=1, c=2, a=3, e=4, re=5

∴ Tenemos A ^-1 = $\begin{pmatrix} 1 & 2 & 3&4&5\\ 3&1&2&5&4 \end{pmatrix}$

Ejemplo 3-: Si $f=\begin {pmatrix} 1 & 2 & 3&4&5\\ 1 & 5& 3&2&4 \end{pmatrix} and \,\,\, g=\begin{pmatrix} 1 & 2 & 3&4&5\\ 2& 3& 1&5&4 \end{pmatrix}$

luego calcule f ^-1 o g ^-1 .

Solución-:

f ^-1 = $\begin{pmatrix} 1 & 2 & 3&4&5\\ 1 & 4 & 3&5&2 \end{pmatrix}$

g ^-1 = $\begin{pmatrix} 1 & 2 & 3&4&5\\ 3 & 1 & 2&5&4 \end{pmatrix}$

f ^-1 o g ^-1 = $\begin{pmatrix} 1 & 2 & 3&4&5\\ 1 & 4 & 3&5&2 \end{pmatrix} o\begin{pmatrix} 1 & 2 & 3&4&5\\ 3 & 1 & 2&5&4 \end{pmatrix}$

f ^-1 o g ^-1 = $\begin{pmatrix} 1 & 2 & 3&4&5\\ 3 & 5 & 2&4&1 \end{pmatrix}$

Ejemplo 4-: Si P1= $\begin{pmatrix} 1 & 2 & 3\\ 3 & 1 & 2 \end{pmatrix}$ , P2= $\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix}$ ,P3= $\begin{pmatrix} 1 & 2 & 3\\ 3 & 2 & 1 \end{pmatrix}$

Encuentre (P1 o P2) ^-1 y (P2 o P3) ^-1 .

Solución-: P1 o P2= $\begin{pmatrix} 1 & 2 & 3\\ 3 & 1 & 2 \end{pmatrix}o\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix}$

P2 o P3= $\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix}o\begin{pmatrix} 1 & 2 & 3\\ 3 & 2 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 2 & 1 & 3 \end{pmatrix}$

Además, sabemos que si P ^-1 es la inversa de la permutación P, entonces P ^-1 o P = I .

∴ (P1 o P2) ^-1 = inversa de $\begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 1 & 2 & 3 \end{pmatrix}$

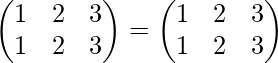
∴ (P2 o P3) ^-1 = inversa de $\begin{pmatrix} 1 & 2 & 3\\ 2 & 1 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 2 & 1 & 3 \end{pmatrix}$

Ejemplo 5-: Demostrar que (1 2 3 ……. n ) ^-1 = ( n n-1 n-3 ….. 2 1)

Solución-: ( 1 2 3 ….. n)= $\begin{pmatrix} 1 & 2 & 3&.......&n-1&n\\ 2 & 3 & 4&.......&n&1 \end{pmatrix}$

= $\begin{pmatrix} 1 & 2 & 3&.......&n-1&n\\ 2 & 3 & 4&.......&n&1 \end{pmatrix}o\begin{pmatrix} n & n-1 &.......&3&2&1\\ n-1 & n-2&.......&2&1&n \end{pmatrix}$

= $\begin{pmatrix} 1 & 2 & 3&.......&n-1&n\\ 2 & 3 & 4&.......&n&1 \end{pmatrix}o\begin{pmatrix} 2 & 3 &.......&n&n-1\\ 1 & 2 &.......&n-1&n \end{pmatrix}$

= $\begin{pmatrix} 1 & 2 &.......&n-1&n\\ 1 & 2 &.......&n-1&n \end{pmatrix}$ = yo

Por lo tanto, (1 2 3 ……. n ) ^-1 = ( n n-1 n-3 ….. 2 1)

Publicación traducida automáticamente

Artículo escrito por portalpirate y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta