Prerrequisito – Grupo
Isomorfismo :
Para dos grupos ( G ,+) y ( G’ ,*) una función f : G → G’ se llama isomorfismo si
- f es uno-uno
- fi s en
- fi s homomorfismo es decir f (a + b) = f( a) * f (b) ∀ a, b ∈ G.
En resumen, un homomorfismo biyectivo es un isomorfismo.
Grupo isomorfo:
Si existe un isomorfismo del grupo (G,+) al (G’,*). Entonces un grupo (G,+) se llama isomorfo a un grupo (G’,*)
Se escribe como G ≅ G’ .
Ejemplos –
1. f(x)=log(x) para grupos (R + ,*) y (R,+) es un isomorfismo de grupo.
Explicación –
- f(x)=f(y) => log(x)=log(y) => x=y , entonces f es uno-uno.
- f(R + )=R , entonces f es sobre.
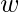
- f(x*y)=log(x*y)=log(x)+log(y)=f(x)+f(y) , entonces f es un homomorfismo.
2. f(x)=ax para el grupo (Z,+) a (aZ,+) , donde a es cualquier número distinto de cero.
Explicación –
- f(x)=f(y) => ax=ay => x=y , entonces f es uno-uno.
- f(Z)=aZ , entonces f es sobre.
- f(x + y) =ax + ay= f(x) + f(y), entonces f es un homomorfismo.
3. La función f del grupo de raíces cúbicas de la unidad { ![]() } con una operación de multiplicación es un isomorfismo para agrupar clases residuales mod(3) {{0},{1},{2}} con la operación de suma de clases residuales mod(3) tal que f(1)={0}, f(
} con una operación de multiplicación es un isomorfismo para agrupar clases residuales mod(3) {{0},{1},{2}} con la operación de suma de clases residuales mod(3) tal que f(1)={0}, f( ![]() )={1} y f(
)={1} y f( ![]() )={2}.
)={2}.
Explicación –
- Claramente, f es sobre y uno-uno.
- También f(1*
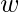 ) = f(
) = f( 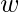 ) = {1} = {0} + 3 {1} = f(1)*f(
) = {1} = {0} + 3 {1} = f(1)*f( 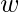 ).
).
f(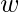 *
* 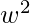 ) = f(1) = {0} = {1} + 3 {2} = f(
) = f(1) = {0} = {1} + 3 {2} = f( 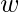 )*f(
)*f( 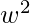 ).
).
y f(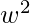 *1) = f(
*1) = f( 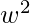 ) = {2}={2} + 3 {0} = f(
) = {2}={2} + 3 {0} = f( 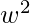 )*f(1). Entonces f es homomorfismo.
)*f(1). Entonces f es homomorfismo.
Todo esto prueba que f es un isomorfismo para dos grupos referidos.
4. f(x)=ex para grupos (R,+) y (R+,*) donde R+ es un grupo de números reales positivos y x es un número entero.
5. Los grupos ({0,1,2,3},+ 4 ) y ({2,3,4,1},+ 5 ) son isomorfos.
NOTA :
- Si hay un Homomorfismo f forman grupos (G,*) a (H,+) . Entonces f también es un isomorfismo si y solo si Ker(f)={e}. Aquí e es la identidad de (G,*).
Además, Ker(f) = Núcleo de un homeomorfismo f :(G,*) → (H,+) es un conjunto de todos los elementos en G tal que una imagen de todos estos elementos en H es el elemento identidad e’ de (H,+) . - Si dos grupos son isomorfos, ambos serán abelianos o no lo serán. Recuerda que un grupo es abeliano si es conmutativo.
- Un conjunto de grupos isomorfos forman una clase de equivalencia y tienen una estructura idéntica y se dice que son abstractamente idénticos.
Automorfismo :
Para un grupo (G,+), una aplicación f : G → G se llama automorfismo si
- f es uno-uno.
- f homomórfica , es decir , f (a +b) = f (a) + f (b) ∀ a, b ∈ G.
Ejemplos –
1. Para cualquier grupo (G,+) un mapeo de identidad I g : G → G, tal que I g (g)=g , ∀g ∈ G es un automorfismo.
Explicación-
- como si I(a)=I(b) => a=b entonces I es uno-uno.
- como I(a+b) =a+b =I(a)+I(b), entonces I también es un homomorfismo.
2. f(x)=-x para el grupo (Z,+).
Explicación-
- como si f(a)=f(b) => -a=-b => a=b entonces f es uno-uno.
- como si f(a+b) =-(a+b) =(-a)+(-b) =f(a)+f(b), entonces f es también un homomorfismo.
3. f(x)=axa -1 para un grupo (G,+) ∀a ∈ G.
Explicación –
- como f(n)=f(m) => ana -1 = ama -1 => n = m entonces f es uno-uno.
- como f(n+m)= a(n+m)a -1 =ana -1 + ama -1 = f(n) + f(m), entonces f es también homomorhismo.
4. f(z)= ![]() para grupos de números complejos con operación de suma.
para grupos de números complejos con operación de suma.
Recuerde que f es un complejo conjugado tal que si z=a+ib entonces f(z)= ![]() =
= ![]() =a-ib.
=a-ib.
5.f(x)=1/x es automorfismo para un grupo (G,*) si es abeliano.
NOTA :
- Un conjunto de todos los automorfismos (funciones) de un grupo, con un compuesto de funciones como operaciones binarias forma un grupo.
- Simplemente, un isomorfismo también se llama automorfismo si tanto el dominio como el rango son iguales.
- Si f es un automorfismo del grupo (G,+), entonces (G,+) es un grupo abeliano.
- El mapeo de identidad como vemos, en el ejemplo, es un automorfismo sobre un grupo que se llama automorfismo trivial y otro no trivial.
- El automorfismo se puede dividir en automorfismo interno y externo .
Publicación traducida automáticamente
Artículo escrito por ohiamvaibhav y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA