k elementos más pequeños en el mismo orden usando O(1) espacio extra

Se nos da una array de n elementos, debe encontrar los k elementos más pequeños de la array, pero deben estar en el mismo orden en que están en la array dada y se nos permite usar solo O (1) espacio adicional.

Ejemplos:  

Input : arr[] = {4, 2, 6, 1, 5}, 
            k = 3
Output : 4 2 1
Explanation : 1, 2 and 4 are three smallest 
numbers and 4 2 1 is their order in given array

Input : arr[] = {4, 12, 16, 21, 25}, 
            k = 3
Output : 4 12 16
Explanation : 4, 12 and 16 are 3 smallest numbers
and 4 12 16 is their order in given arra
 

Hemos discutido una solución eficiente para encontrar los n elementos más pequeños del problema anterior usando espacio extra de O(n). Para resolverlo sin utilizar ningún espacio extra, utilizaremos el concepto de ordenación por inserción.
La idea es mover k elementos mínimos para empezar en el mismo orden. Para hacer esto, comenzamos desde el (k+1)-ésimo elemento y nos movemos hasta el final. Para cada elemento de la array, reemplazamos el elemento más grande de los primeros k elementos con el elemento actual si el elemento actual es más pequeño que el más grande. Para mantener el orden, usamos la idea  de ordenar por inserción .

El diagrama de flujo es el siguiente: 

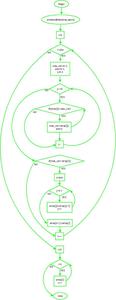
Diagrama de flujo- printsmall

 Implementación:

// CPP for printing smallest k numbers in order
 
#include <algorithm>
#include <iostream>
using namespace std;
 
// Function to print smallest k numbers
// in arr[0..n-1]
void printSmall(int arr[], int n, int k)
{
    // For each arr[i] find whether
    // it is a part of n-smallest
    // with insertion sort concept
    for (int i = k; i < n; ++i) {
 
        // find largest from first k-elements
        int max_var = arr[k - 1];
        int pos = k - 1;
 
        for (int j = k - 2; j >= 0; j--) {
            if (arr[j] > max_var) {
                max_var = arr[j];
                pos = j;
            }
        }
 
        // if largest is greater than arr[i]
        // shift all element one place left
        if (max_var > arr[i]) {
 
            int j = pos;
            while (j < k - 1) {
                arr[j] = arr[j + 1];
                j++;
            }
 
            // make arr[k-1] = arr[i]
            arr[k - 1] = arr[i];
        }
    }
 
    // print result
    for (int i = 0; i < k; i++)
        cout << arr[i] << " ";
}
 
// Driver program
int main()
{
    int arr[] = { 1, 5, 8, 9, 6, 7, 3, 4, 2, 0 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int k = 5;
    printSmall(arr, n, k);
    return 0;
}

// Java for printing smallest k numbers in order
import java.lang.*;
import java.util.*;
 
public class GfG {
    // Function to print smallest k numbers
    // in arr[0..n-1]
    public static void printSmall(int arr[], int n, int k)
    {
        // For each arr[i] find whether
        // it is a part of n-smallest
        // with insertion sort concept
        for (int i = k; i < n; ++i) {
            // Find largest from top n-element
            int max_var = arr[k - 1];
            int pos = k - 1;
            for (int j = k - 2; j >= 0; j--) {
                if (arr[j] > max_var) {
                    max_var = arr[j];
                    pos = j;
                }
            }
 
            // If largest is greater than arr[i]
            // shift all element one place left
            if (max_var > arr[i]) {
                int j = pos;
                while (j < k - 1) {
                    arr[j] = arr[j + 1];
                    j++;
                }
                // make arr[k-1] = arr[i]
                arr[k - 1] = arr[i];
            }
        }
        // print result
        for (int i = 0; i < k; i++)
            System.out.print(arr[i] + " ");
    }
 
    // Driver function
    public static void main(String argc[])
    {
        int[] arr = { 1, 5, 8, 9, 6, 7, 3, 4, 2, 0 };
        int n = 10;
        int k = 5;
        printSmall(arr, n, k);
    }
}

# Python 3 for printing smallest
# k numbers in order
 
# Function to print smallest k
# numbers in arr[0..n-1]
 
 
def printSmall(arr, n, k):
 
    # For each arr[i] find whether
    # it is a part of n-smallest
    # with insertion sort concept
    for i in range(k, n):
 
        # find largest from first k-elements
        max_var = arr[k - 1]
        pos = k - 1
        for j in range(k - 2, -1, -1):
 
            if (arr[j] > max_var):
 
                max_var = arr[j]
                pos = j
 
        # if largest is greater than arr[i]
        # shift all element one place left
        if (max_var > arr[i]):
 
            j = pos
            while (j < k - 1):
 
                arr[j] = arr[j + 1]
                j += 1
 
            # make arr[k-1] = arr[i]
            arr[k - 1] = arr[i]
 
    # print result
    for i in range(0, k):
        print(arr[i], end=" ")
 
 
# Driver program
arr = [1, 5, 8, 9, 6, 7, 3, 4, 2, 0]
n = len(arr)
k = 5
printSmall(arr, n, k)

// C# for printing smallest k numbers in order
using System;
 
public class GfG {
 
    // Function to print smallest k numbers
    // in arr[0..n-1]
    public static void printSmall(int[] arr, int n, int k)
    {
 
        // For each arr[i] find whether
        // it is a part of n-smallest
        // with insertion sort concept
        for (int i = k; i < n; ++i) {
 
            // Find largest from top n-element
            int max_var = arr[k - 1];
            int pos = k - 1;
            for (int j = k - 2; j >= 0; j--) {
                if (arr[j] > max_var) {
                    max_var = arr[j];
                    pos = j;
                }
            }
 
            // If largest is greater than arr[i]
            // shift all element one place left
            if (max_var > arr[i]) {
                int j = pos;
                while (j < k - 1) {
                    arr[j] = arr[j + 1];
                    j++;
                }
 
                // make arr[k-1] = arr[i]
                arr[k - 1] = arr[i];
            }
        }
 
        // print result
        for (int i = 0; i < k; i++)
            Console.Write(arr[i] + " ");
    }
 
    // Driver function
    public static void Main()
    {
 
        int[] arr = { 1, 5, 8, 9, 6, 7, 3, 4, 2, 0 };
        int n = 10;
        int k = 5;
 
        printSmall(arr, n, k);
    }
}

<?php
// PHP for printing smallest
// k numbers in order
 
// Function to print smallest k
// numbers in arr[0..n-1]
function printSmall($arr, $n, $k)
{
     
    // For each arr[i] find whether
    // it is a part of n-smallest
    // with insertion sort concept
    for ($i = $k; $i < $n; ++$i)
    {
         
        // find largest from
        // first k-elements
        $max_var = $arr[$k - 1];
        $pos = $k - 1;
        for ($j = $k - 2; $j >= 0; $j--)
        {        
            if ($arr[$j] > $max_var)
            {
                $max_var = $arr[$j];
                $pos = $j;
            }
        }
 
        // if largest is greater than arr[i]
        // shift all element one place left
        if ($max_var > $arr[$i])
        {
            $j = $pos;
            while ($j < $k - 1)
            {
                $arr[$j] = $arr[$j + 1];
                $j++;
            }
             
            // make arr[k - 1] = arr[i]
            $arr[$k - 1] = $arr[$i];
        }
    }
     
    // print result
    for ($i = 0; $i < $k; $i++)
    echo $arr[$i] ," ";
                 
}
     
    // Driver Code
    $arr = array(1, 5, 8, 9, 6, 7, 3, 4, 2, 0);
    $n = count($arr);
    $k = 5;
    printSmall($arr, $n, $k);
     
 
?>

<script>
 
// JavaScript program for printing smallest k numbers in order
  
    // Function to print smallest k numbers
    // in arr[0..n-1]
    function printSmall(arr, n, k)
    {
        // For each arr[i] find whether
        // it is a part of n-smallest
        // with insertion sort concept
        for (let i = k; i < n; ++i) {
            // Find largest from top n-element
            let max_var = arr[k - 1];
            let pos = k - 1;
            for (let j = k - 2; j >= 0; j--) {
                if (arr[j] > max_var) {
                    max_var = arr[j];
                    pos = j;
                }
            }
   
            // If largest is greater than arr[i]
            // shift all element one place left
            if (max_var > arr[i]) {
                let j = pos;
                while (j < k - 1) {
                    arr[j] = arr[j + 1];
                    j++;
                }
                // make arr[k-1] = arr[i]
                arr[k - 1] = arr[i];
            }
        }
        // print result
        for (let i = 0; i < k; i++)
            document.write(arr[i] + " ");
    }
 
  
// Driver code          
    let arr = [ 1, 5, 8, 9, 6, 7, 3, 4, 2, 0 ];
    let n = 10;
    let k = 5;
    printSmall(arr, n, k);
     
   
</script>

1 3 4 2 0