Recomendamos leer las siguientes publicaciones como requisito previo para esta publicación.
K’th elemento más pequeño/más grande en array no ordenada | Establecer 1
k’ésimo elemento más pequeño/más grande en array sin clasificar | Conjunto 2 (Tiempo lineal esperado)
Dada una array y un número k donde k es más pequeño que el tamaño de la array, necesitamos encontrar el k-ésimo elemento más pequeño en la array dada. Se da que todos los elementos de la array son distintos.
Ejemplos:
Input: arr[] = {7, 10, 4, 3, 20, 15}
k = 3
Output: 7
Input: arr[] = {7, 10, 4, 3, 20, 15}
k = 4
Output: 10
En la publicación anterior , discutimos un algoritmo de tiempo lineal esperado. En esta publicación, se analiza un método de tiempo lineal en el peor de los casos. La idea de este nuevo método es similar a quickSelect(). Obtenemos el tiempo lineal en el peor de los casos seleccionando un pivote que divide la array de manera equilibrada (no hay muy pocos elementos en un lado y muchos en el otro lado) . Después de que la array se divida de manera equilibrada, aplicamos los mismos pasos que usamos en quickSelect() para decidir si ir a la izquierda o a la derecha del pivote.
El siguiente es el algoritmo completo.
kthSmallest(arr[0..n-1], k)
1) Divida arr[] en ⌈n/5⌉ grupos donde el tamaño de cada grupo es 5 excepto posiblemente el último grupo que puede tener menos de 5 elementos.
2) Ordene los ⌈n/5⌉ grupos creados anteriormente y encuentre la mediana de todos los grupos. Cree una array auxiliar ‘median[]’ y almacene las medianas de todos los grupos ⌈n/5⌉ en esta array mediana.
// Llame recursivamente a este método para encontrar la mediana de la mediana [0..⌈n/5⌉-1]
3) medOfMed = kthSmallest(median[0..⌈n/5⌉-1], ⌈n/10⌉)
4 ) Particionar arr[] alrededor de medOfMed y obtener su posición.
pos = partición(arr, n, medOfMed)
5) Si pos == k devuelve medOfMed
6) Si pos > k devuelve kthSmallest(arr[l..pos-1], k)
7)Si pos < k devuelve kthSmallest(arr[pos+1..r], k-pos+l-1)
En el algoritmo anterior, los últimos 3 pasos son los mismos que el algoritmo de la publicación anterior . Los primeros cuatro pasos se usan para obtener un buen punto para particionar la array (para asegurarse de que no haya demasiados elementos a cada lado del pivote).
A continuación se muestra la implementación del algoritmo anterior.
C++
// C++ implementation of worst case linear time algorithm
// to find k'th smallest element
#include<iostream>
#include<algorithm>
#include<climits>
using namespace std;
int partition(int arr[], int l, int r, int k);
// A simple function to find median of arr[]. This is called
// only for an array of size 5 in this program.
int findMedian(int arr[], int n)
{
sort(arr, arr+n); // Sort the array
return arr[n/2]; // Return middle element
}
// Returns k'th smallest element in arr[l..r] in worst case
// linear time. ASSUMPTION: ALL ELEMENTS IN ARR[] ARE DISTINCT
int kthSmallest(int arr[], int l, int r, int k)
{
// If k is smaller than number of elements in array
if (k > 0 && k <= r - l + 1)
{
int n = r-l+1; // Number of elements in arr[l..r]
// Divide arr[] in groups of size 5, calculate median
// of every group and store it in median[] array.
int i, median[(n+4)/5]; // There will be floor((n+4)/5) groups;
for (i=0; i<n/5; i++)
median[i] = findMedian(arr+l+i*5, 5);
if (i*5 < n) //For last group with less than 5 elements
{
median[i] = findMedian(arr+l+i*5, n%5);
i++;
}
// Find median of all medians using recursive call.
// If median[] has only one element, then no need
// of recursive call
int medOfMed = (i == 1)? median[i-1]:
kthSmallest(median, 0, i-1, i/2);
// Partition the array around a random element and
// get position of pivot element in sorted array
int pos = partition(arr, l, r, medOfMed);
// If position is same as k
if (pos-l == k-1)
return arr[pos];
if (pos-l > k-1) // If position is more, recur for left
return kthSmallest(arr, l, pos-1, k);
// Else recur for right subarray
return kthSmallest(arr, pos+1, r, k-pos+l-1);
}
// If k is more than number of elements in array
return INT_MAX;
}
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// It searches for x in arr[l..r], and partitions the array
// around x.
int partition(int arr[], int l, int r, int x)
{
// Search for x in arr[l..r] and move it to end
int i;
for (i=l; i<r; i++)
if (arr[i] == x)
break;
swap(&arr[i], &arr[r]);
// Standard partition algorithm
i = l;
for (int j = l; j <= r - 1; j++)
{
if (arr[j] <= x)
{
swap(&arr[i], &arr[j]);
i++;
}
}
swap(&arr[i], &arr[r]);
return i;
}
// Driver program to test above methods
int main()
{
int arr[] = {12, 3, 5, 7, 4, 19, 26};
int n = sizeof(arr)/sizeof(arr[0]), k = 3;
cout << "K'th smallest element is "
<< kthSmallest(arr, 0, n-1, k);
return 0;
}
Java
// Java implementation of worst
// case linear time algorithm
// to find k'th smallest element
import java.util.*;
class GFG
{
// int partition(int arr[], int l, int r, int k);
// A simple function to find median of arr[]. This is called
// only for an array of size 5 in this program.
static int findMedian(int arr[], int i,int n)
{
Arrays.sort(arr, i, n);
return arr[i+(n-i)/2]; // sort the array and return middle element
}
// Returns k'th smallest element
// in arr[l..r] in worst case
// linear time. ASSUMPTION: ALL
// ELEMENTS IN ARR[] ARE DISTINCT
static int kthSmallest(int arr[], int l, int r, int k)
{
// If k is smaller than
// number of elements in array
if (k > 0 && k <= r - l + 1)
{
int n = r - l + 1 ; // Number of elements in arr[l..r]
// Divide arr[] in groups of size 5,
// calculate median of every group
// and store it in median[] array.
int i;
// There will be floor((n+4)/5) groups;
int []median = new int[(n + 4) / 5];
for (i = 0; i < n/5; i++)
median[i] = findMedian(arr, l+i*5, l+i*5+5);
// For last group with less than 5 elements
if (i*5 < n)
{
median[i] = findMedian(arr, l+i*5, l+i*5+n%5);
i++;
}
// Find median of all medians using recursive call.
// If median[] has only one element, then no need
// of recursive call
int medOfMed = (i == 1)? median[i - 1]:
kthSmallest(median, 0, i - 1, i / 2);
// Partition the array around a random element and
// get position of pivot element in sorted array
int pos = partition(arr, l, r, medOfMed);
// If position is same as k
if (pos-l == k - 1)
return arr[pos];
if (pos-l > k - 1) // If position is more, recur for left
return kthSmallest(arr, l, pos - 1, k);
// Else recur for right subarray
return kthSmallest(arr, pos + 1, r, k - pos + l - 1);
}
// If k is more than number of elements in array
return Integer.MAX_VALUE;
}
static int[] swap(int []arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
return arr;
}
// It searches for x in arr[l..r], and
// partitions the array around x.
static int partition(int arr[], int l,
int r, int x)
{
// Search for x in arr[l..r] and move it to end
int i;
for (i = l; i < r; i++)
if (arr[i] == x)
break;
swap(arr, i, r);
// Standard partition algorithm
i = l;
for (int j = l; j <= r - 1; j++)
{
if (arr[j] <= x)
{
swap(arr, i, j);
i++;
}
}
swap(arr, i, r);
return i;
}
// Driver code
public static void main(String[] args)
{
int arr[] = {12, 3, 5, 7, 4, 19, 26};
int n = arr.length, k = 3;
System.out.println("K'th smallest element is "
+ kthSmallest(arr, 0, n - 1, k));
}
}
// This code has been contributed by 29AjayKumar and updated by ajayhajare
Python3
# Python3 implementation of worst case
# linear time algorithm to find
# k'th smallest element
# Returns k'th smallest element in arr[l..r]
# in worst case linear time.
# ASSUMPTION: ALL ELEMENTS IN ARR[] ARE DISTINCT
def kthSmallest(arr, l, r, k):
# If k is smaller than number of
# elements in array
if (k > 0 and k <= r - l + 1):
# Number of elements in arr[l..r]
n = r - l + 1
# Divide arr[] in groups of size 5,
# calculate median of every group
# and store it in median[] array.
median = []
i = 0
while (i < n // 5):
median.append(findMedian(arr, l + i * 5, 5))
i += 1
# For last group with less than 5 elements
if (i * 5 < n):
median.append(findMedian(arr, l + i * 5,
n % 5))
i += 1
# Find median of all medians using recursive call.
# If median[] has only one element, then no need
# of recursive call
if i == 1:
medOfMed = median[i - 1]
else:
medOfMed = kthSmallest(median, 0,
i - 1, i // 2)
# Partition the array around a medOfMed
# element and get position of pivot
# element in sorted array
pos = partition(arr, l, r, medOfMed)
# If position is same as k
if (pos - l == k - 1):
return arr[pos]
if (pos - l > k - 1): # If position is more,
# recur for left subarray
return kthSmallest(arr, l, pos - 1, k)
# Else recur for right subarray
return kthSmallest(arr, pos + 1, r,
k - pos + l - 1)
# If k is more than the number of
# elements in the array
return 999999999999
def swap(arr, a, b):
temp = arr[a]
arr[a] = arr[b]
arr[b] = temp
# It searches for x in arr[l..r],
# and partitions the array around x.
def partition(arr, l, r, x):
for i in range(l, r):
if arr[i] == x:
swap(arr, r, i)
break
x = arr[r]
i = l
for j in range(l, r):
if (arr[j] <= x):
swap(arr, i, j)
i += 1
swap(arr, i, r)
return i
# A simple function to find
# median of arr[] from index l to l+n
def findMedian(arr, l, n):
lis = []
for i in range(l, l + n):
lis.append(arr[i])
# Sort the array
lis.sort()
# Return the middle element
return lis[n // 2]
# Driver Code
if __name__ == '__main__':
arr = [12, 3, 5, 7, 4, 19, 26]
n = len(arr)
k = 3
print("K'th smallest element is",
kthSmallest(arr, 0, n - 1, k))
# This code is contributed by Ashutosh450
C#
// C# implementation of worst
// case linear time algorithm
// to find k'th smallest element
using System;
class GFG
{
// int partition(int arr[], int l, int r, int k);
// A simple function to find median of arr[]. This is called
// only for an array of size 5 in this program.
static int findMedian(int []arr, int i, int n)
{
if(i <= n)
Array.Sort(arr, i, n); // Sort the array
else
Array.Sort(arr, n, i);
return arr[n/2]; // Return middle element
}
// Returns k'th smallest element
// in arr[l..r] in worst case
// linear time. ASSUMPTION: ALL
// ELEMENTS IN ARR[] ARE DISTINCT
static int kthSmallest(int []arr, int l,
int r, int k)
{
// If k is smaller than
// number of elements in array
if (k > 0 && k <= r - l + 1)
{
int n = r - l + 1 ; // Number of elements in arr[l..r]
// Divide arr[] in groups of size 5,
// calculate median of every group
// and store it in median[] array.
int i;
// There will be floor((n+4)/5) groups;
int []median = new int[(n + 4) / 5];
for (i = 0; i < n/5; i++)
median[i] = findMedian(arr, l + i * 5, 5);
// For last group with less than 5 elements
if (i*5 < n)
{
median[i] = findMedian(arr,l + i * 5, n % 5);
i++;
}
// Find median of all medians using recursive call.
// If median[] has only one element, then no need
// of recursive call
int medOfMed = (i == 1)? median[i - 1]:
kthSmallest(median, 0, i - 1, i / 2);
// Partition the array around a random element and
// get position of pivot element in sorted array
int pos = partition(arr, l, r, medOfMed);
// If position is same as k
if (pos-l == k - 1)
return arr[pos];
if (pos-l > k - 1) // If position is more, recur for left
return kthSmallest(arr, l, pos - 1, k);
// Else recur for right subarray
return kthSmallest(arr, pos + 1, r, k - pos + l - 1);
}
// If k is more than number of elements in array
return int.MaxValue;
}
static int[] swap(int []arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
return arr;
}
// It searches for x in arr[l..r], and
// partitions the array around x.
static int partition(int []arr, int l,
int r, int x)
{
// Search for x in arr[l..r] and move it to end
int i;
for (i = l; i < r; i++)
if (arr[i] == x)
break;
swap(arr, i, r);
// Standard partition algorithm
i = l;
for (int j = l; j <= r - 1; j++)
{
if (arr[j] <= x)
{
swap(arr, i, j);
i++;
}
}
swap(arr, i, r);
return i;
}
// Driver code
public static void Main(String[] args)
{
int []arr = {12, 3, 5, 7, 4, 19, 26};
int n = arr.Length, k = 3;
Console.WriteLine("K'th smallest element is "
+ kthSmallest(arr, 0, n - 1, k));
}
}
// This code contributed by Rajput-Ji
Javascript
<script>
// Javascript implementation of worst
// case linear time algorithm
// to find k'th smallest element
// int partition(int arr[], int l, int r, int k);
// A simple function to find median of arr[]. This is called
// only for an array of size 5 in this program.
function findMedian(arr, i, n) {
if (i <= n)
arr.sort((a, b) => a - b); // Sort the array
else
arr.sort((a, b) => a - b);
return arr[Math.floor(n / 2)]; // Return middle element
}
// Returns k'th smallest element
// in arr[l..r] in worst case
// linear time. ASSUMPTION: ALL
// ELEMENTS IN ARR[] ARE DISTINCT
function kthSmallest(arr, l, r, k)
{
// If k is smaller than
// number of elements in array
if (k > 0 && k <= r - l + 1)
{
let n = r - l + 1; // Number of elements in arr[l..r]
// Divide arr[] in groups of size 5,
// calculate median of every group
// and store it in median[] array.
let i;
// There will be floor((n+4)/5) groups;
let median = new Array(Math.floor((n + 4) / 5));
for (i = 0; i < n / 5; i++)
median[i] = findMedian(arr, l + i * 5, 5);
// For last group with less than 5 elements
if (i * 5 < n)
{
median[i] = findMedian(arr, l + i * 5, n % 5);
i++;
}
// Find median of all medians using recursive call.
// If median[] has only one element, then no need
// of recursive call
let medOfMed = (i == 1) ? median[i - 1] :
kthSmallest(median, 0, i - 1, Math.floor(i / 2));
// Partition the array around a random element and
// get position of pivot element in sorted array
let pos = partition(arr, l, r, medOfMed);
// If position is same as k
if (pos - l == k - 1)
return arr[pos];
if (pos - l > k - 1) // If position is more, recur for left
return kthSmallest(arr, l, pos - 1, k);
// Else recur for right subarray
return kthSmallest(arr, pos + 1, r, k - pos + l - 1);
}
// If k is more than number of elements in array
return Integer.MAX_VALUE;
}
function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
return arr;
}
// It searches for x in arr[l..r], and
// partitions the array around x.
function partition(arr, l, r, x) {
// Search for x in arr[l..r] and move it to end
let i;
for (i = l; i < r; i++)
if (arr[i] == x)
break;
swap(arr, i, r);
// Standard partition algorithm
i = l;
for (let j = l; j <= r - 1; j++) {
if (arr[j] <= x) {
swap(arr, i, j);
i++;
}
}
swap(arr, i, r);
return i;
}
// Driver code
let arr = [12, 3, 5, 7, 4, 19, 26];
let n = arr.length, k = 3;
document.write("K'th smallest element is "
+ kthSmallest(arr, 0, n - 1, k));
// This code has been contributed by Saurabh Jaiswal
</script>
Producción:
K'th smallest element is 5
Complejidad de tiempo:
La complejidad de tiempo en el peor de los casos del algoritmo anterior es O(n). Analicemos todos los pasos.
Los pasos (1) y (2) toman un tiempo O(n) ya que encontrar la mediana de una array de tamaño 5 toma un tiempo O(1) y hay n/5 arrays de tamaño 5.
El paso (3) toma T(n/5 ) tiempo. El paso (4) es una partición estándar y toma tiempo O(n).
Los pasos interesantes son 6) y 7). A lo sumo, uno de ellos es ejecutado. Estos son pasos recursivos. ¿Cuál es el tamaño en el peor de los casos de estas llamadas recursivas? La respuesta es el número máximo de elementos mayores que medOfMed (obtenido en el paso 3) o el número máximo de elementos menores que medOfMed.
¿Cuántos elementos son mayores que medOfMed y cuántos son más pequeños?
Al menos la mitad de las medianas encontradas en el paso 2 son mayores o iguales a medOfMed. Así, al menos la mitad de los n/5 grupos aportan 3 elementos mayores que medOfMed, excepto el grupo que tiene menos de 5 elementos. Por lo tanto, el número de elementos mayor que medOfMed es al menos. ![]()
De manera similar, la cantidad de elementos que son menores que medOfMed es al menos 3n/10 – 6. En el peor de los casos, la función se repite como máximo n – (3n/10 – 6), que es 7n/10 + 6 elementos.
Tenga en cuenta que 7n/10 + 6 < 20 y que cualquier entrada de 80 elementos o menos requiere un tiempo O(1). Por lo tanto, podemos obtener la recurrencia 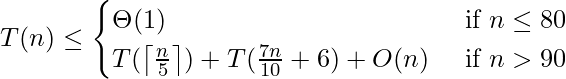
Demostramos que el tiempo de ejecución es lineal por sustitución. Suponga que T(n) cn para alguna constante c y todo n > 80. Sustituyendo esta hipótesis inductiva en el lado derecho de la recurrencia se obtiene
T(n) <= cn/5 + c(7n/10 + 6) + O(n)
<= cn/5 + c + 7cn/10 + 6c + O(n)
<= 9cn/10 + 7c + O(n)
<= cn,
ya que podemos elegir c lo suficientemente grande como para que c(n/10 – 7) sea mayor que la función descrita por el término O(n) para todo n > 80. Por lo tanto, el tiempo de ejecución en el peor de los casos es lineal (Fuente: http ://staff.ustc.edu.cn/~csli/graduate/algorithms/book6/chap10.htm ).
Tenga en cuenta que el algoritmo anterior es lineal en el peor de los casos, pero las constantes son muy altas para este algoritmo. Por lo tanto, este algoritmo no funciona bien en situaciones prácticas; random quickSelect funciona mucho mejor y es el preferido.
Fuentes:
videoconferencia del MIT sobre estadísticas de pedidos, mediana
introducción a los algoritmos por Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L.
http://staff.ustc.edu.cn/~csli/graduate/algorithms/book6 /chap10.htm
Este artículo es una contribución de Shivam . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
