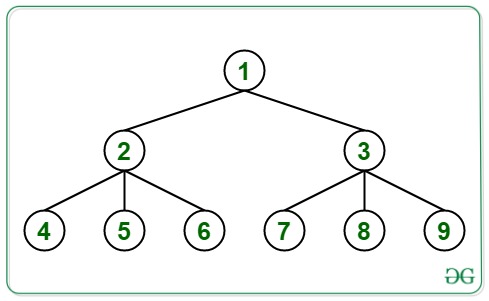
Dado un árbol N-ario y un entero K , la tarea es imprimir los Kth ancestros de todos los Nodes del árbol en orden de nivel. Si los ancestros K no existen para un Node, imprima -1 para ese Node.
Ejemplos:
Entrada: K = 2
Salida: -1 -1 -1 1 1 1 1 1 1
Explicación:
el segundo antepasado no existe para los Nodes 1, 2 y 3 El
segundo antepasado de los Nodes 4, 5, 6, 7, 8, 9 es 1 .Entrada: K = 1
Salida: -1 1 1 2 2 2 3 3 3
Enfoque: El enfoque es usar DFS para encontrar los ancestros de todos los Nodes. A continuación se muestran los pasos:
- El K -ésimo padre de cualquier Node se puede encontrar usando DFS y almacenando todos los padres de un Node en un vector temporal, digamos temp[] .
- Cada vez que se visita un Node en DFS , se inserta en el vector temporal .
- Al final de DFS , el Node visitado actualmente se extrae del vector temporal .
- Para el Node visitado actualmente, el vector contiene todos los ancestros del Node.
- El K -ésimo Node desde el final del vector es el K -ésimo ancestro del Node visitado actualmente, así que guárdelo en una array ancestro[] .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation of
// the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to add an
// edge in the tree
void addEdge(vector<int> v[],
int x, int y)
{
v[x].push_back(y);
v[y].push_back(x);
}
// DFS to find the Kth
// ancestor of every node
void dfs(vector<int> tree[],
vector<int>& temp,
int ancestor[], int u,
int parent, int k)
{
// Pushing current node
// in the vector
temp.push_back(u);
// Traverse its neighbors
for (auto i : tree[u]) {
if (i == parent)
continue;
dfs(tree, temp,
ancestor, i, u, k);
}
temp.pop_back();
// If K ancestors are not
// found for current node
if (temp.size() < k) {
ancestor[u] = -1;
}
else {
// Add the Kth ancestor
// for the node
ancestor[u]
= temp[temp.size() - k];
}
}
// Function to find Kth
// ancestor of each node
void KthAncestor(int N, int K, int E,
int edges[][2])
{
// Building the tree
vector<int> tree[N + 1];
for (int i = 0; i < E; i++) {
addEdge(tree, edges[i][0],
edges[i][1]);
}
// Stores all parents of a node
vector<int> temp;
// Store Kth ancestor
// of all nodes
int ancestor[N + 1];
dfs(tree, temp, ancestor, 1, 0, K);
// Print the ancestors
for (int i = 1; i <= N; i++) {
cout << ancestor[i] << " ";
}
}
int main()
{
// Given N and K
int N = 9;
int K = 2;
// Given edges of n-ary tree
int E = 8;
int edges[8][2] = { { 1, 2 }, { 1, 3 }, { 2, 4 },
{ 2, 5 }, { 2, 6 }, { 3, 7 },
{ 3, 8 }, { 3, 9 } };
// Function Call
KthAncestor(N, K, E, edges);
return 0;
}
Java
// Java implementation of
// the above approach
import java.util.*;
class GFG{
// Function to add an
// edge in the tree
static void addEdge(Vector<Integer> v[],
int x, int y)
{
v[x].add(y);
v[y].add(x);
}
// DFS to find the Kth
// ancestor of every node
static void dfs(Vector<Integer> tree[],
Vector<Integer> temp,
int ancestor[], int u,
int parent, int k)
{
// Pushing current node
// in the vector
temp.add(u);
// Traverse its neighbors
for(int i : tree[u])
{
if (i == parent)
continue;
dfs(tree, temp,
ancestor, i, u, k);
}
temp.remove(temp.size() - 1);
// If K ancestors are not
// found for current node
if (temp.size() < k)
{
ancestor[u] = -1;
}
else
{
// Add the Kth ancestor
// for the node
ancestor[u] = temp.get(temp.size() - k);
}
}
// Function to find Kth
// ancestor of each node
static void KthAncestor(int N, int K, int E,
int edges[][])
{
// Building the tree
@SuppressWarnings("unchecked")
Vector<Integer> []tree = new Vector[N + 1];
for(int i = 0; i < tree.length; i++)
tree[i] = new Vector<Integer>();
for(int i = 0; i < E; i++)
{
addEdge(tree, edges[i][0],
edges[i][1]);
}
// Stores all parents of a node
Vector<Integer> temp = new Vector<Integer>();
// Store Kth ancestor
// of all nodes
int []ancestor = new int[N + 1];
dfs(tree, temp, ancestor, 1, 0, K);
// Print the ancestors
for(int i = 1; i <= N; i++)
{
System.out.print(ancestor[i] + " ");
}
}
// Driver code
public static void main(String[] args)
{
// Given N and K
int N = 9;
int K = 2;
// Given edges of n-ary tree
int E = 8;
int edges[][] = { { 1, 2 }, { 1, 3 },
{ 2, 4 }, { 2, 5 },
{ 2, 6 }, { 3, 7 },
{ 3, 8 }, { 3, 9 } };
// Function call
KthAncestor(N, K, E, edges);
}
}
// This code is contributed by Amit Katiyar
Python3
# Python3 implementation of # the above approach # Function to add an # edge in the tree def addEdge(v, x, y): v[x].append(y) v[y].append(x) # DFS to find the Kth # ancestor of every node def dfs(tree, temp, ancestor, u, parent, k): # Pushing current node # in the vector temp.append(u) # Traverse its neighbors for i in tree[u]: if (i == parent): continue dfs(tree, temp, ancestor, i, u, k) temp.pop() # If K ancestors are not # found for current node if (len(temp) < k): ancestor[u] = -1 else: # Add the Kth ancestor # for the node ancestor[u] = temp[len(temp) - k] # Function to find Kth # ancestor of each node def KthAncestor(N, K, E, edges): # Building the tree tree = [[] for i in range(N + 1)] for i in range(E): addEdge(tree, edges[i][0], edges[i][1]) # Stores all parents of a node temp = [] # Store Kth ancestor # of all nodes ancestor = [0] * (N + 1) dfs(tree, temp, ancestor, 1, 0, K) # Print the ancestors for i in range(1, N + 1): print(ancestor[i], end = " ") # Driver code if __name__ == '__main__': # Given N and K N = 9 K = 2 # Given edges of n-ary tree E = 8 edges = [ [ 1, 2 ], [ 1, 3 ], [ 2, 4 ], [ 2, 5 ], [ 2, 6 ], [ 3, 7 ], [ 3, 8 ], [ 3, 9 ] ] # Function call KthAncestor(N, K, E, edges) # This code is contributed by mohit kumar 29
C#
// C# implementation of
// the above approach
using System;
using System.Collections.Generic;
class GFG{
// Function to add an
// edge in the tree
static void addEdge(List<int> []v,
int x, int y)
{
v[x].Add(y);
v[y].Add(x);
}
// DFS to find the Kth
// ancestor of every node
static void dfs(List<int> []tree,
List<int> temp,
int []ancestor, int u,
int parent, int k)
{
// Pushing current node
// in the vector
temp.Add(u);
// Traverse its neighbors
foreach(int i in tree[u])
{
if (i == parent)
continue;
dfs(tree, temp,
ancestor, i, u, k);
}
temp.RemoveAt(temp.Count - 1);
// If K ancestors are not
// found for current node
if (temp.Count < k)
{
ancestor[u] = -1;
}
else
{
// Add the Kth ancestor
// for the node
ancestor[u] = temp[temp.Count - k];
}
}
// Function to find Kth
// ancestor of each node
static void KthAncestor(int N, int K, int E,
int [,]edges)
{
// Building the tree
List<int> []tree = new List<int>[N + 1];
for(int i = 0; i < tree.Length; i++)
tree[i] = new List<int>();
for(int i = 0; i < E; i++)
{
addEdge(tree, edges[i, 0],
edges[i, 1]);
}
// Stores all parents of a node
List<int> temp = new List<int>();
// Store Kth ancestor
// of all nodes
int []ancestor = new int[N + 1];
dfs(tree, temp, ancestor, 1, 0, K);
// Print the ancestors
for(int i = 1; i <= N; i++)
{
Console.Write(ancestor[i] + " ");
}
}
// Driver code
public static void Main(String[] args)
{
// Given N and K
int N = 9;
int K = 2;
// Given edges of n-ary tree
int E = 8;
int [,]edges = { { 1, 2 }, { 1, 3 },
{ 2, 4 }, { 2, 5 },
{ 2, 6 }, { 3, 7 },
{ 3, 8 }, { 3, 9 } };
// Function call
KthAncestor(N, K, E, edges);
}
}
// This code is contributed by Amit Katiyar
Javascript
<script>
// JavaScript program for the above approach
// Function to add an
// edge in the tree
function addEdge(v, x, y)
{
v[x].push(y);
v[y].push(x);
}
// DFS to find the Kth
// ancestor of every node
function dfs(tree, temp, ancestor, u, parent, k)
{
// Pushing current node
// in the vector
temp.push(u);
// Traverse its neighbors
for(let i = 0; i < tree[u].length; i++)
{
if (tree[u][i] == parent)
continue;
dfs(tree, temp, ancestor, tree[u][i], u, k);
}
temp.pop();
// If K ancestors are not
// found for current node
if (temp.length < k)
{
ancestor[u] = -1;
}
else
{
// Add the Kth ancestor
// for the node
ancestor[u] = temp[temp.length - k];
}
}
// Function to find Kth
// ancestor of each node
function KthAncestor(N, K, E, edges)
{
// Building the tree
let tree = new Array(N + 1);
for(let i = 0; i < tree.length; i++)
tree[i] = [];
for(let i = 0; i < E; i++)
{
addEdge(tree, edges[i][0], edges[i][1]);
}
// Stores all parents of a node
let temp = [];
// Store Kth ancestor
// of all nodes
let ancestor = new Array(N + 1);
dfs(tree, temp, ancestor, 1, 0, K);
// Print the ancestors
for(let i = 1; i <= N; i++)
{
document.write(ancestor[i] + " ");
}
}
// Given N and K
let N = 9;
let K = 2;
// Given edges of n-ary tree
let E = 8;
let edges = [ [ 1, 2 ], [ 1, 3 ],
[ 2, 4 ], [ 2, 5 ],
[ 2, 6 ], [ 3, 7 ],
[ 3, 8 ], [ 3, 9 ] ];
// Function call
KthAncestor(N, K, E, edges);
</script>
-1 -1 -1 1 1 1 1 1 1
Complejidad temporal: O(N)
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por DiptayanBiswas y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA