La cubierta del juego es NP Complete

Problema : Dado un Conjunto base X , un entero k , y una colección de subconjuntos Si de X _, el problema es identificar si existe una colección de subconjuntos cuya unión sea X , con tamaño a lo sumo k .

Prueba: una instancia del problema es una entrada especificada para el problema. Una instancia del problema Set Cover es un Ground set X, un entero k y una colección de subconjuntos Si formada a partirde X. Dado que un problema NP-completo , por definición, es un problema que es tanto NP como NP-Difícil , la prueba o afirmación de que un problema es NP-Completo consta de dos partes:

1. El problema en sí es NP-Complete.
2. Todos los demás problemas en la clase NP pueden ser reducibles en tiempo polinomial a eso. (B es poli-tiempo reducible a C).

Si se cumple la única segunda condición, el problema se llama NP-Hard. Pero no es posible reducir cada problema NP a otro problema NP para mostrar su NP-Completitud todo el tiempo. Es por eso que si queremos mostrar que un problema es NP-completo, demuestre que el problema está en NP y cualquier problema NP-Completo es reducible a eso. Así, se puede verificar que el problema de cobertura de conjuntos es NP-Completo usando las siguientes proposiciones:

1. Set Cover está en NP: si algún problema está en NP , entonces dado un ‘certificado’, que es una solución al problema y una instancia del problema (una colección de subconjuntos, C de tamaño k), podremos identificar (si la solución es correcta o no) certificado en tiempo polinomial. Esto se puede hacer:
   Proporcionar una colección C de subconjuntos de tamaño k , podemos iterar sobre cada elemento en los subconjuntos de la colección y marcar los elementos en X que están cubiertos. Al final, no se deben descubrir elementos en X.
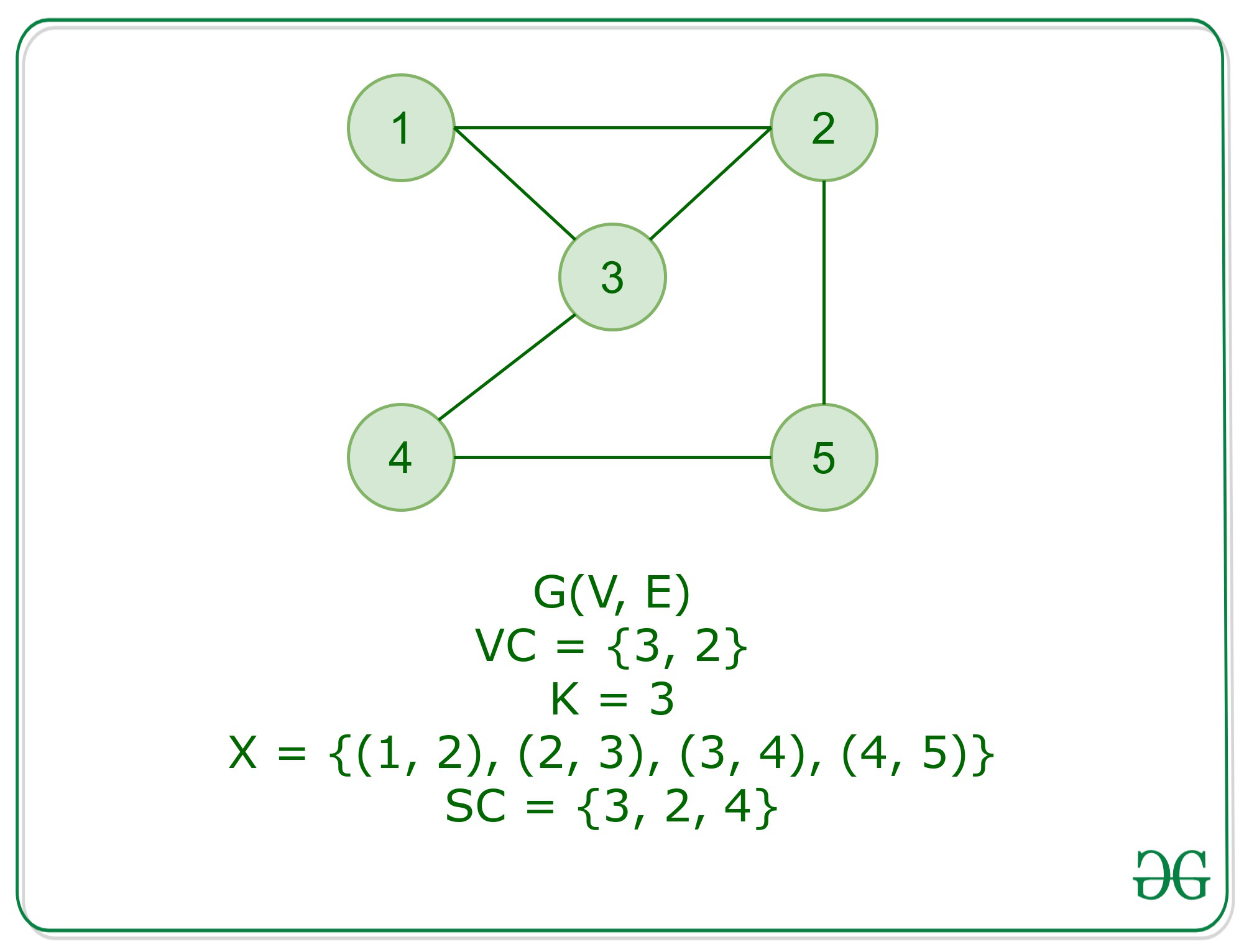
   Esto toma un tiempo polinomial con respecto al número de subconjuntos en X. Por lo tanto, Set Cover está en NP.
2. Set Cover es NP-Hard: Para probar que set cover es NP Hard, realizaremos una reducción de un problema NP-Hard conocido, es decir, cobertura de vértice para establecer el problema de cobertura. Para el problema de cobertura de vértice, tenemos como entrada un gráfico G = (V, E) y un número entero k. Ahora, deja que el suelo se asiente
   • X = E, ese es el conjunto de aristas en G.
   • El subconjunto S _u para cada vértice u en V , contiene las aristas incidentes a u .

Ahora bien, se cumplen las siguientes dos proposiciones:

• Consideremos que los k conjuntos S _u1 , S _u2 ……S _uk cubren el conjunto base X , luego cada borde e en E es adyacente al mínimo un vértice desde u1…uk, por lo tanto formando una cubierta de vértice de tamaño k .
• Consideremos que los vértices u1…uk forman una cubierta de vértices, entonces Su1 cubre todas las aristas incidentes en u1. Por lo tanto, la colección de conjuntos S _u1 , S _u2 …S _uk forman el conjunto cubierta que cubre X .

Conclusión:

es NP-completo