Introducción | Curva de dragón
Una curva de dragón es una curva recursiva que no se cruza, también conocida como el dragón de Harter-Heighway o la curva del dragón de Jurassic Park. Es una curva matemática que se puede aproximar mediante métodos recursivos como los sistemas de Lindenmayer. Sistemas de Lindenmayer: un sistema de Lindenmayer, también conocido como sistema L, es un sistema de reescritura de strings que se puede utilizar para generar fractales. Dos áreas principales incluyen la generación de fractales y el modelado realista de plantas. El sistema de Lindenmayer comienza con una string de símbolos llamada axioma y aplica al axioma un conjunto de reglas de producción que se utilizan para reescribir el axioma. El sistema L recursivo es más interesante ya que reemplaza un símbolo con una copia de sí mismo más algo extra. El sistema L sigue algunas reglas:
An L-system is a formal grammar consisting of 4 parts: 1. A set of variables: symbols that can be replaced by production rules. 2. A set of constants: symbols that do not get replaced.e.g: !, [, ], +, -. 3. A single axiom: a string & is the initial state of the system. 4. A set of production rules: defining the way/rule variables can be replaced.
Tomemos el ejemplo del siguiente sistema L: Reglas del sistema L
| Sistema L de recursividad | |
|---|---|
| axioma | skk |
| normas | s = ksk |
| generación 1: | (ksk)kk = kskkk |
| generación 2: | k(ksk)kkk = kkskkkk |
| generación 3: | kk(ksk)kkkk = kkskkkkk |
gen 1 takes help of gen 0 (axiom) generation 1 -> apply rule in generation 0 generation 0 = skk replace s with "ksk" in gen 0 to get gen 1 gen 1 = (s)kk = (ksk)kk = kskskk replace s with "ksk" in gen 1 to get gen 2 Iterate the same rule for all generations
Los sistemas L recursivos a menudo producen patrones intrincadamente complejos que son autosimilares en múltiples escalas. Estos patrones complejos se pueden visualizar con la ayuda de una interpretación gráfica aplicada a los sistemas L basada en gráficos de turtle. Cuando los sistemas L se utilizan con turtle gráficos, un estado de la Turtle se define como un cuádruple (x, y, a, c). Las coordenadas cartesianas (x, y) representan la posición de la Turtle. El ángulo a, llamado rumbo, se interpreta como la dirección en la que mira la Turtle. El color c se interpreta como el rotulador de color que la Turtle ha presionado actualmente contra el suelo para que cualquier movimiento de la Turtle cree una línea de ese color. Dado el tamaño del paso d y el incremento del ángulo b, la Turtle puede responder a los símbolos en una string del sistema L de acuerdo con las siguientes instrucciones:
Move forward (in the dir of the current heading) a distance d while drawing a line of color c. The state of the turtle changes to (x', y', a, c), where x' = x + d cos(a) and y' = y + d sin(a)
Sistema Dragon Curve L
La aproximación finita de la curva Dragon se puede crear con un sistema L. El sistema L de la curva Dragon se puede representar como:
| Sistema Dragon Curve L | |
|---|---|
| variables: | fh |
| constantes: | + – |
| axioma: | F |
| normas: | f = fh h = f+h |
| incremento de ángulo: | 90 grados |
| generación 1: | fh |
| generación 2: | fh – f+h |
| generación 3: | fh – f+h – fh + f+h |
| generación 4: | fh – f+h – fh + f+h – fh – f+h + fh + f+h |
2 rules
/ \
replace f with f-h replace h with f+h
+ & - are constants
build up generations by following rules on axiom
gen 1 forms gen 2; gen 2 forms gen 3 and so on...
The generation 2 string is: 'f-h - f+h'
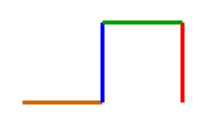 In the above L-system, assuming that the initial heading of the turtle is upward on the screen, then the first ‘f’ will draw a line straight up. The ‘-‘ causes the turtle to change its heading by 90 degrees to be pointed directly to the left. The ‘h’ draws a line directly to the left of the screen. The second ‘-‘ symbol again turns the turtle 90 degrees to its left which is directly down on the screen. The f symbol draws a unit length line in the down direction. The last turn symbol in the string is a ‘+’ which turns the turtle to its right by 90 degrees. However, since current heading of the turtle is pointed downward, its right is the screen’s left, so again the turtle’s heading is to the left of the screen. Finally, the h symbol draws a unit length line to the screen’s left.Hence we get the colorful resulting image. If we keep on forming more generations, we get beautiful curves called the dragon curves.As we can see below, the curve gets more intricate and complex as we grow in generations. Iteration 3:
In the above L-system, assuming that the initial heading of the turtle is upward on the screen, then the first ‘f’ will draw a line straight up. The ‘-‘ causes the turtle to change its heading by 90 degrees to be pointed directly to the left. The ‘h’ draws a line directly to the left of the screen. The second ‘-‘ symbol again turns the turtle 90 degrees to its left which is directly down on the screen. The f symbol draws a unit length line in the down direction. The last turn symbol in the string is a ‘+’ which turns the turtle to its right by 90 degrees. However, since current heading of the turtle is pointed downward, its right is the screen’s left, so again the turtle’s heading is to the left of the screen. Finally, the h symbol draws a unit length line to the screen’s left.Hence we get the colorful resulting image. If we keep on forming more generations, we get beautiful curves called the dragon curves.As we can see below, the curve gets more intricate and complex as we grow in generations. Iteration 3:  Iteration 9:
Iteration 9: 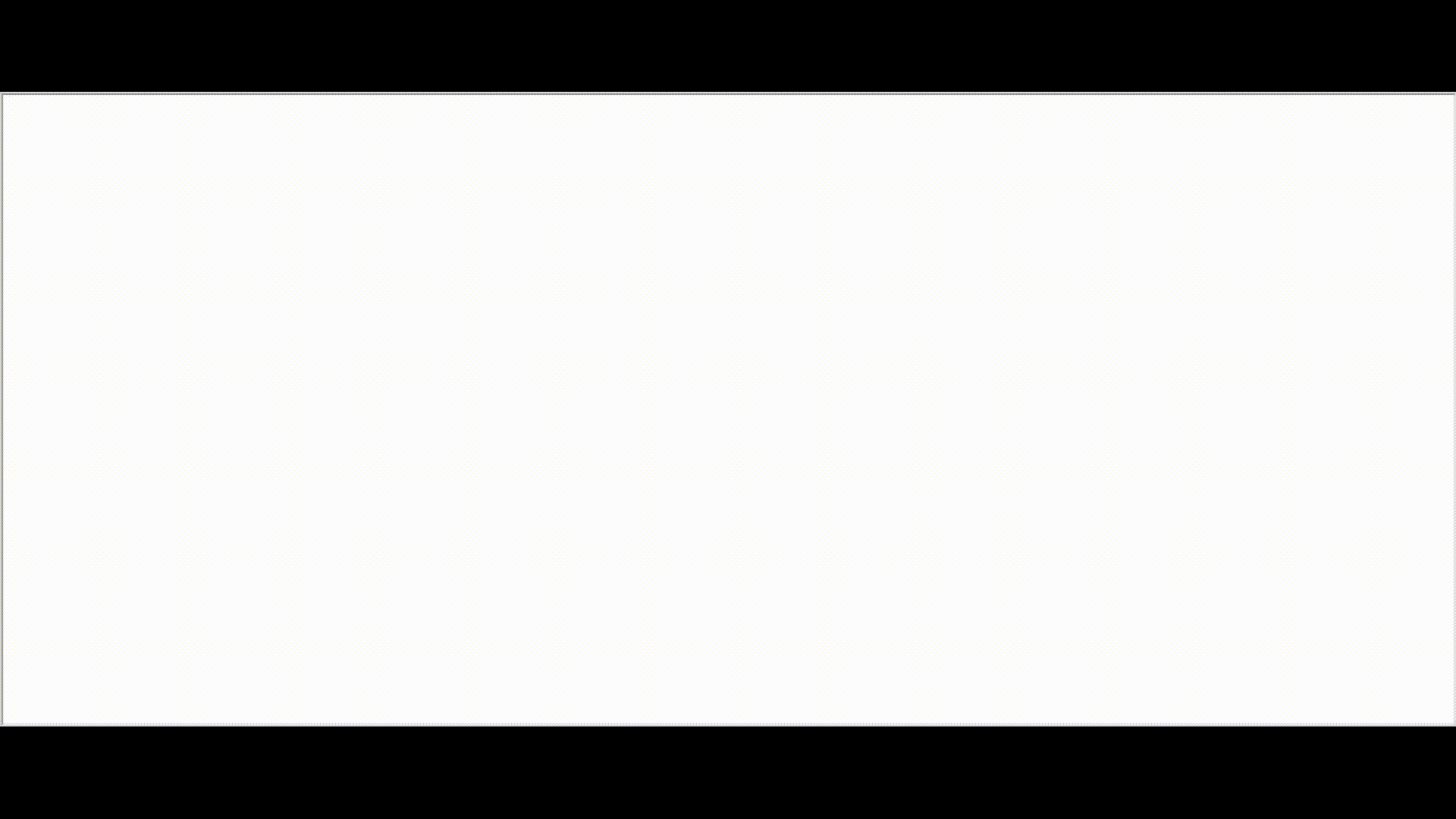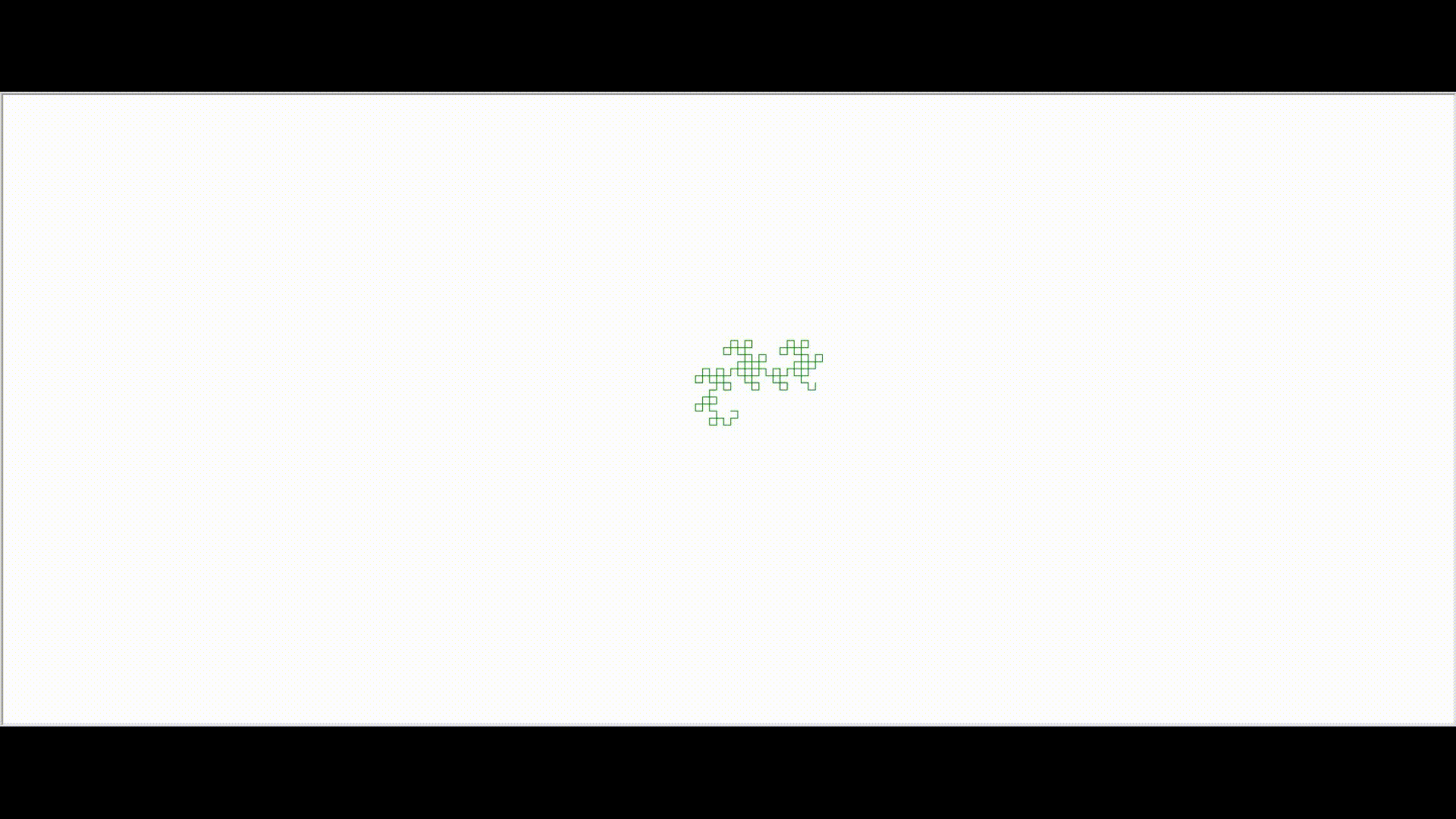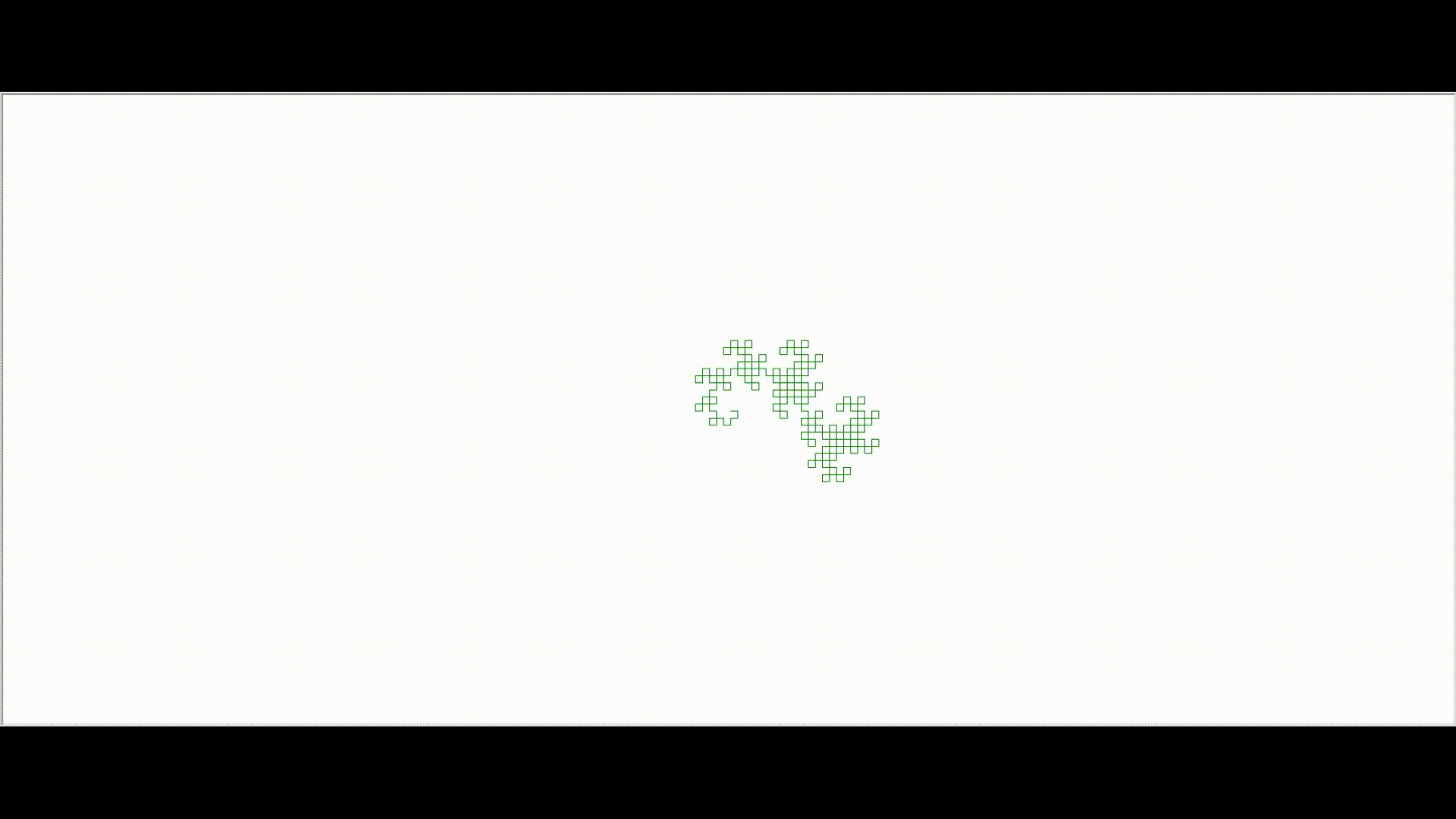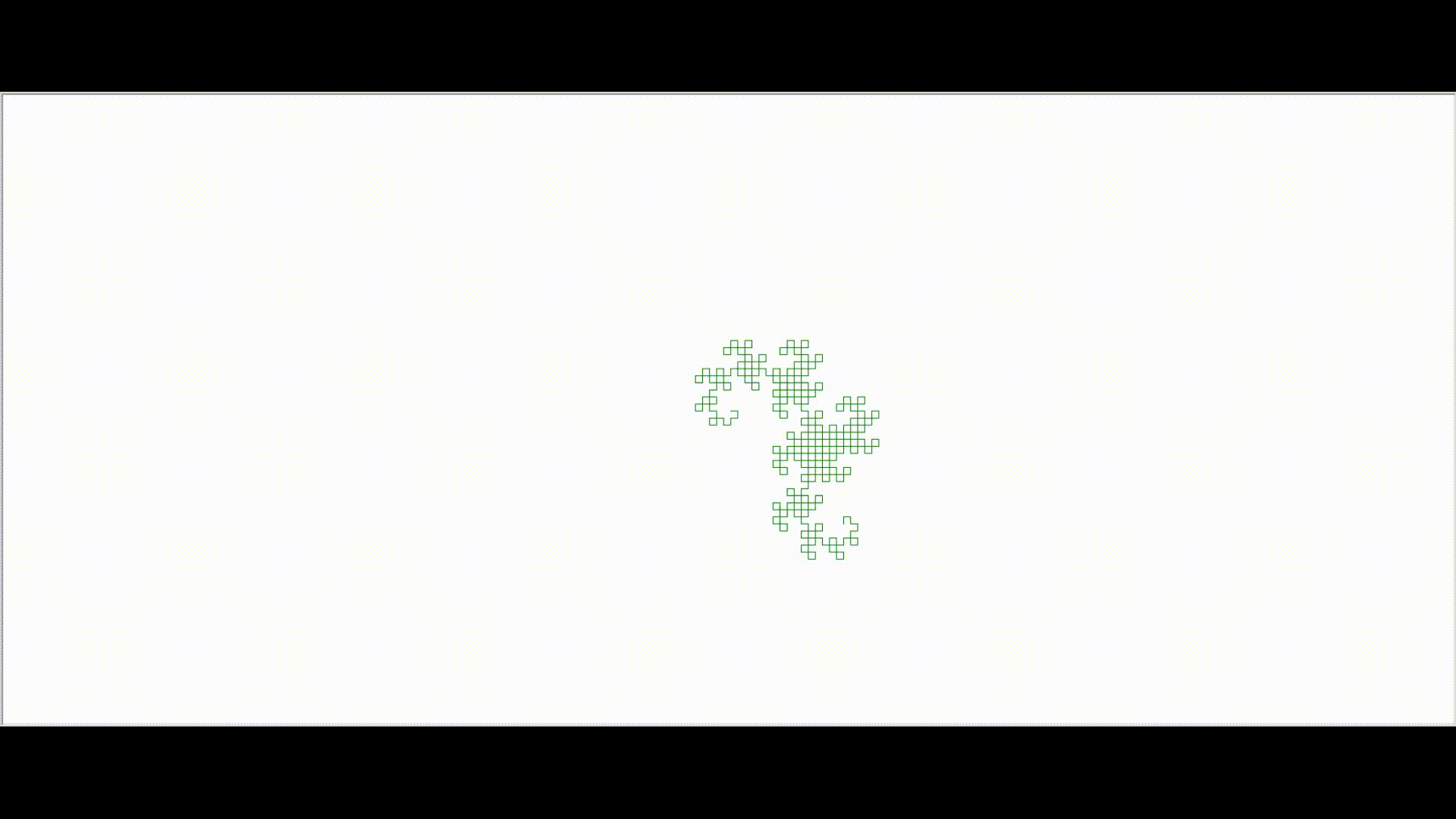
Dragon Curve usando papel
Estas curvas de dragón también se pueden formar mediante plegado de papel: el concepto es muy simple pero el potencial es asombroso. Tome una tira larga de papel y dóblela por la mitad. ¡Obtienes una tira de papel con un pliegue! Vuelva a doblar el papel y luego dóblelo por la mitad nuevamente. Cuando miras dentro, tienes dos pliegues que van en una dirección y un pliegue que va en la otra dirección. Vuelve a doblar y dobla por la mitad otra vez y, cuando desdoblas, obtienes aún más pliegues, algunos en una dirección, otros en la otra. Desdoble la tira y haga un pliegue firme a lo largo de cada una de las líneas de pliegue, teniendo cuidado de mantener la dirección correcta del pliegue. Coloca la tira sobre su borde, con cada pliegue formando un ángulo de 90 grados, y mírala hacia abajo. Verá un patrón intrincado de cuadrados y giros y vueltas. Las tiras reciben el nombre de Dragon Curves porque, después de algunos pliegues,Numberphile explica bien la formación de Dragon Curve en su video. También puedes ver las transiciones de Dragon Curve aquí:
Programando la curva del dragón
PSEUDOCODE
→ IMPORT TURTLE
→ TURN TURTLE - RIGHT SIDE('r') #OLD PATTERN = 'r'
→ NEW PATTERN = OLD PATTERN
→ USER INPUT [ Number of Iterations(n), Segment size, Pen color & Background color ]
→ CYCLE = 1
→ WHILE CYCLE < ITERATION :
→ FORM DRAGON CURVE L-SYSTEM
→ STORE THE PATTERN OF 'l'/'r' in NEW PATTERN
→ NEW PATTERN += OLD PATTERN
→ OLD PATTERN = NEW PATTERN
→ INCREMENT CYCLE
→ USER INPUT [Whether to display 'r'/'l' Dragon curve L-system in console]
→ INITIATE THE TURTLE TO DRAW [pencolor, bgcolor, draw right = segment size]
→ ITERATE OVER FULL L SYSTEM FOR n ITERATIONS:
→ IF CHAR == 'r'
→ DRAW RIGHT(90)
→ DRAW FORWARD(Segment Size)
→ ELSE IF CHAR == 'l'
→ DRAW LEFT(90)
→ DRAW FORWARD(Segment Size)
→ END
Python
# import the turtle module to use turtle graphics
import turtle
# make variables for the right and left containing 'r' and 'l'
r = 'r'
l = 'l'
# assign our first iteration a right so we can build off of it
old = r
new = old
# for inputs
iteration = int(input('Enter iteration:'))
length = int(input('Enter length of each segment:'))
pencolor = input('Enter pen color:')
bgcolor = input('Enter background color:')
# set the number of times we have been creating
# the next iteration as the first
cycle = 1
# keep on generating the next iteration until desired iteration is reached
while cycle<iteration:
# add a right to the end of the old iteration and save it to the new
new = (old) + (r)
# flip the old iteration around(as in the first character becomes last)
old = old[::-1]
# cycling through each character in the flipped old iteration:
for char in range(0, len(old)):
# if the character is a right:
if old[char] == r:
# change it to a left
old = (old[:char])+ (l) + (old[char + 1:])
# otherwise, if it's a left:
elif old[char] == l:
#change it to a right
old = (old[:char]) + (r) + (old[char + 1:])
# add the modified old to the new iteration
new = (new) + (old)
# save the new iteration to old as well for use next cycle
old = new
# advance cycle variable to keep track of the number of times it's been done
cycle = cycle + 1
printans = input('Display r/l form?(y/n):')
if printans =='y':
print(new)
# for not show the turtle icon when drawing
turtle.ht()
turtle.speed(0)
turtle.color(pencolor)
turtle.bgcolor(bgcolor)
turtle.forward(length)
# cycling through all the characters in the iteration
for char in range(0, len(new)):
# if the character is a right:
if new[char] == (r):
turtle.right(90)
turtle.forward(length)
# otherwise, if the character is a left:
elif new[char] == (l):
turtle.left(90)
turtle.forward(length)
Producción :
Obtenga los códigos de Dragon curve para diferentes idiomas de rosettacode . Le dará mucho placer comprobar los fractales usted mismo. Consulte también, Proyecto Euler: Problema 220 : Heighway Dragon . Referencias:
- Matemáticas de la formación de Fractales
- matemáticas.psu.edu [pdf]
- ecademy.agnesscott.edu
- pensamientoslanudos.com
Este artículo es una contribución de Amartya Ranjan Saikia . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA