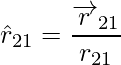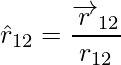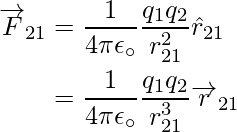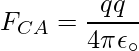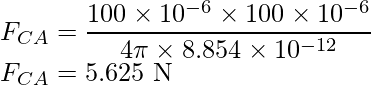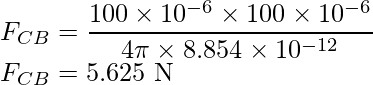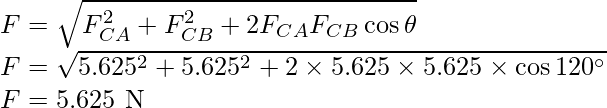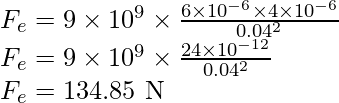Ley de Coulomb

Cuando nos quitamos la ropa sintética o el suéter de nuestro cuerpo, especialmente en clima seco, aparece una chispa o un crujido. Con ropa femenina como un sari de poliéster, esto es casi inevitable. Los relámpagos, en el cielo durante las tormentas eléctricas, son otro caso de descarga eléctrica. Es una descarga eléctrica que siempre sentimos al abrir la puerta de un automóvil o agarrar la barra de hierro de un autobús después de deslizarnos de nuestros asientos.

La causa de estas sensaciones es la descarga de cargas eléctricas que se han acumulado como consecuencia del roce de superficies aislantes. Esto se debe a la generación de electricidad estática. Cualquier cosa que no tenga movimiento o cambio con el tiempo se denomina estática. El estudio de las fuerzas, campos y potenciales provenientes de cargas estáticas se conoce como Electrostática .

Comprendamos ahora una de las leyes básicas e importantes de la electrostática llamada Ley de Coulomb como:

La ley de Coulomb es una fórmula matemática que describe la fuerza entre dos cargas puntuales. Cuando el tamaño de los cuerpos cargados es sustancialmente más pequeño que la separación entre ellos, entonces el tamaño no se considera o puede ignorarse. Los cuerpos cargados pueden considerarse como cargas puntuales.

La fuerza de atracción o repulsión entre dos cosas cargadas es directamente proporcional al producto de sus cargas e inversamente proporcional al cuadrado de la distancia que las separa, según la ley de Coulomb . Actúa a lo largo de la línea que conecta las dos cargas que se consideran cargas puntuales.

Coulomb estudió la fuerza entre dos cargas puntuales y encontró que es inversamente proporcional al cuadrado de la distancia entre ellas, directamente proporcional al producto de sus magnitudes y actuando en una línea que las conecta.

Fórmula de la ley de Coulomb

La cantidad de la fuerza (F) entre dos cargas puntuales q ₁ y q ₂ separadas por una distancia r en el vacío está dada por,

F ∝ q ₁ q ₂

y

F ∝ 1/r ²

o

F ∝ q ₁ q ₂ / r ²

o

F = kq ₁ q ₂ / r ²

donde k es la constante de proporcionalidad y es igual a 1/4πε ₀ .

El símbolo ε ₀ se llama épsilon no, y significa permitividad del vacío .

El valor de k es 9 × 10 ⁹ Nm ² / C ² cuando tomamos la unidad SI de valor de ε ₀ que es 8.854 × 10 ^-12 C ² N ^-1 m ^-2 .

Ley de Coulomb en forma vectorial

La ley de Coulomb se escribe mejor en notación vectorial porque la fuerza es una cantidad vectorial. Las cargas q ₁ y q ₂ tienen vectores de ubicación r ₁ y r ₂ , respectivamente. F ₁₂ denota fuerza sobre q ₁ debido a q ₂ y F ₂₁ denota fuerza sobre q ₂ debido a q ₁ . Por conveniencia, las cargas de dos puntos q ₁ y q ₂ se han numerado 1 y 2, respectivamente, y el vector que va de 1 a 2 se ha designado como r ₂₁ .

Geometría y Fuerzas entre cargas.

$\overrightarrow{r}_{21} = \overrightarrow{r}_2- \overrightarrow{r}_1$

De manera similar, el vector que va de 2 a 1 se denota por r _12,

$\overrightarrow{r}_{12} = \overrightarrow{r}_1- \overrightarrow{r}_2$

r ₂₁ y r ₁₂ son las magnitudes de los vectores $\overrightarrow{r}_{21}$ y $\overrightarrow{r}_{12}$ , respectivamente y la magnitud r ₁₂ es igual a r ₂₁ . Un vector unitario a lo largo del vector especifica la dirección del vector. Los vectores unitarios se utilizan para indicar la dirección de 1 a 2 (o de 2 a 1). Los vectores unitarios se definen como,

$\hat{r}_{21}=\dfrac{\overrightarrow{{r}}_{21}}{r_{21}}$

Similarmente,

$\hat{r}_{12}=\dfrac{\overrightarrow{{r}}_{12}}{r_{12}}$

La ley de fuerza de Coulomb entre dos cargas puntuales q ₁ y q ₂ ubicadas en los vectores r ₁ y r ₂ se expresa entonces como,

$\begin{aligned}\overrightarrow{F}_{21}&=\dfrac{1}{4\pi{\epsilon}_\circ}\dfrac{q_1q_2}{{r}_{21}^2}\hat{r}_{21}\\&=\frac{1}{4\pi{\epsilon}_\circ}\frac{q_1q_2}{{r}_{21}^3}\overrightarrow{r}_{21}\end{aligned}$

Puntos clave sobre la ley de Coulomb:

La expresión anterior se cumple independientemente de si q ₁ yq ₂ son positivos o negativos. F ₂₁ es hacia 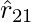$\hat{r}_{21}$ , que fuerza repulsiva, como debería ser para cargas iguales que son si q ₁ y q ₂ son del mismo signo (tanto positivo como negativo). Cuando los signos de q ₁ y q ₂ son opuestos o no les gusta la carga, F ₂₁ es hacia 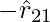$-\hat{r}_{21}$ , hacia 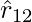$\hat{r}_{12}$ la que muestra atracción, como se esperaba para cargas diferentes. Como resultado, no necesitamos construir ecuaciones separadas para cargas iguales y diferentes. Ambos casos se manejan correctamente mediante la expresión anterior para la ley de fuerza de Coulomb.
La expresión anterior para la ley de fuerza de Coulomb se puede usar para calcular la fuerza F ₁₂ sobre la carga q ₁ debido a la carga q ₂ simplemente intercambiando 1 y 2 como,

$\begin{aligned}\overrightarrow{F}_{21}&=\dfrac{1}{4\pi{\epsilon}_\circ}\dfrac{q_1q_2}{{r}_{21}^2}\hat{r}_{21}\\&=\frac{1}{4\pi{\epsilon}_\circ}\frac{q_1q_2}{{r}_{21}^3}\overrightarrow{r}_{21}\end{aligned}$

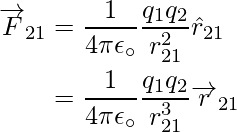
Por lo tanto, la ley de Coulomb concuerda con la tercera ley de Newton.

En el vacío, la expresión de la ley de Coulomb determina la fuerza entre dos cargas q ₁ yq ₂ . Si las cargas están depositadas en materia o hay materia en la zona intermedia, la situación se complica por la presencia de constituyentes de materia cargada.
Dos conductores idénticos con cargas q ₁ y q ₂ se ponen en contacto y luego se separan, lo que da como resultado que cada conductor tenga una carga igual a (q ₁ +q ₂ )/2. Cada carga será igual a (q ₁ -q ₂ )/2 si las cargas son q ₁ y –q ₂ .

Fuerza entre cargas múltiples

Un sistema de tres cargas.

Considere un sistema en el vacío con n inmóviles, es decir, cargas estacionarias q ₁ , q ₂ y q ₃ . Se ha demostrado experimentalmente que la suma vectorial de todas las fuerzas sobre una carga debidas a otras cargas, tomadas una a la vez, es la suma vectorial de todas las fuerzas sobre esa carga debidas a las otras cargas. Debido a la presencia de otras cargas, las fuerzas separadas no se ven afectadas. Esto se conoce como el principio de superposición.

La fuerza sobre una carga, digamos q ₁ , debida a otras dos cargas, q ₂ y q ₃ , puede determinarse realizando una suma vectorial de las fuerzas debidas a cada una de estas cargas. Como resultado, si F ₁₂ denota la fuerza ejercida sobre q ₁ como resultado de q _2,

$\overrightarrow{F}_{12}=\dfrac{1}{4\pi{\epsilon}_\circ}\dfrac{q_1q_2}{{r}_{12}^2}\hat{r}_{12}$

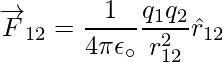
De manera similar, F ₁₃ denota la fuerza ejercida sobre q ₁ como resultado de q _3, que nuevamente es la fuerza de Coulomb sobre q ₁ debida a q ₃ aunque esté presente otra carga q _{2 .}

$\overrightarrow{F}_{13}=\dfrac{1}{4\pi{\epsilon}_\circ}\dfrac{q_1q_3}{{r}_{13}^2}\hat{r}_{13}$

Por lo tanto, la fuerza total F ₁ sobre q ₁ debido a las dos cargas q ₂ y q ₃ se puede expresar como,

$\begin{aligned}\overrightarrow{F}_{1}&=\overrightarrow{F}_{12}+\overrightarrow{F}_{13}\\&=\dfrac{1}{4\pi{\epsilon}_\circ}\dfrac{q_1q_2}{{r}_{12}^2}\hat{r}_{12}+\dfrac{1}{4\pi{\epsilon}_\circ}\dfrac{q_1q_3}{{r}_{13}^2}\hat{r}_{13}\\&=\dfrac{q_1}{4\pi{\epsilon}_\circ}\left[\dfrac{q_2}{{r}_{12}^2}\hat{r}_{12}+\dfrac{q_3}{{r}_{13}^2}\hat{r}_{13}\right]\end{aligned}$

Un sistema de cargas múltiples

El cálculo de fuerza anterior se puede aplicar a un sistema con más de tres cargas. El principio de superposición establece que en un sistema de cargas q ₁ , q _2…….q _n , la fuerza sobre q ₁ debida a q ₂ es igual a la ley de Coulomb, es decir, no se ve afectada por la presencia de otras cargas q ₃ , q ₄ ,…, q _n . La suma vectorial de las fuerzas F ₁₂ , F ₁₃ ,…, F _1n sobre la carga q ₁ debido a todas las demás cargas da la fuerza total F ₁ se puede escribir como

$\overrightarrow{F}_{1}=\overrightarrow{F}_{12}+\overrightarrow{F}_{13}+....+\overrightarrow{F}_{1n}\\ \overrightarrow{F}_{1}=\frac{q_1}{4\pi{\epsilon}_\circ}\left[\frac{q_2}{{r}_{12}^2}\hat{r}_{12}+\frac{q_3}{{r}_{13}^2}\hat{r}_{13}+....+\frac{q_n}{{r}_{1n}^2}\hat{r}_{1n}\right]\\ \overrightarrow{F}_{1}=\frac{q_1}{4\pi{\epsilon}_\circ}\sum_{i=2}^n\frac{q_i}{{r}_{1i}^2}\hat{r}_{1i}$

La suma vectorial se calcula utilizando la ley del paralelogramo de la suma vectorial. La ley de Coulomb y el principio de superposición son los fundamentos de la electrostática.

Limitaciones de la Ley de Coulomb

Sólo las cargas puntuales en reposo están cubiertas por la ley.
La Ley de Coulomb solo es aplicable en situaciones en las que se sigue la ley del cuadrado inverso.
Cuando las cargas tienen una forma arbitraria, es difícil aplicar la ley de Coulomb ya que no se puede determinar la distancia entre ellas.
La carga de los planetas más grandes no se puede calcular directamente usando la ley.

Aplicaciones de la Ley de Coulomb

Calcular la distancia entre las dos cargas así como la fuerza entre ellas.
La ley de Coulombs se puede utilizar para calcular el campo eléctrico que es:

mi = F / _qT

donde E es el campo eléctrico, F es la fuerza y q _T es la carga de prueba.

Su unidad SI es NC ^-1 .

Problemas de muestra

Problema 1: Cargas de 100 microculombios de magnitud cada una están ubicadas en el vacío en las esquinas A, B y C de un triángulo equilátero que mide 4 metros de lado. Si la carga en A y C es positiva y la carga B negativa, ¿cuál es la magnitud y dirección de la fuerza total sobre la carga en C?

Solución:

La Fuerza F _CA se aplica hacia AC y la expresión para la F _CA se expresa como

$F_{CA}=\dfrac{qq}{4\pi{\epsilon}_\circ}$

Sustituya los valores en la expresión anterior,

$F_{CA}=\dfrac{100\times10^{-6}\times100\times10^{-6}}{4\pi\times8.854\times10^{-12}}\\ F_{CA}=5.625\text{ N}$

La Fuerza F _CB se aplica hacia CB y la expresión para la F _CB se expresa como

$F_{CB}=\dfrac{qq}{4\pi{\epsilon}_\circ}$

Sustituya los valores en la expresión anterior,

$F_{CB}=\dfrac{100\times10^{-6}\times100\times10^{-6}}{4\pi\times8.854\times10^{-12}}\\ F_{CB}=5.625\text{ N}$

Por lo tanto, las dos fuerzas son iguales en magnitud pero en diferentes direcciones. El ángulo entre ellos es de 120º. La fuerza resultante F está dada por,

$F=\sqrt{F_{CA}^2+F_{CB}^2+2F_{CA}F_{CB}\cos\theta}\\ F=\sqrt{5.625^2+5.625^2+2\times5.625\times5.625\times\cos120^\circ}\\ F=5.625\text{ N}$

Problema 2: Una carga positiva de 6×10 ^-6 C está a 0,040 m de la segunda carga positiva de 4×10 ^-6 C. Calcula la fuerza entre las cargas.

Solución:

Dado,

Una carga positiva q ₁ es 6×10 ^-6 C.

La segunda carga positiva q ₂ es 4×10 ^-6 C.

La distancia entre las cargas r es de 0,040 m.

$F_e=k\frac{q_1q_2}{r^2}$

Sustituya los valores en la expresión anterior,

$F_e=9\times10^9\times\frac{6\times10^{-6}\times4\times10^{-6}}{0.04^2}\\F_e=9\times10^9\times\frac{24\times10^{-12}}{0.04^2} \\F_e=134.85\text{ N}$

Problema 3: Enunciar la ley de Coulomb y su expresión.

Solución:

La ley de Coulomb es una fórmula matemática que describe la fuerza entre dos cargas puntuales. Cuando el tamaño de los cuerpos cargados es sustancialmente más pequeño que la separación entre ellos, entonces el tamaño no se considera o puede ignorarse. Los cuerpos cargados pueden considerarse como cargas puntuales. Coulomb estudió la fuerza entre dos cargas puntuales y encontró que es inversamente proporcional al cuadrado de la distancia entre ellas, directamente proporcional al producto de sus magnitudes y actuando en una línea que las conecta.

La cantidad de fuerza (F) entre dos cargas puntuales q ₁ y q ₂ separadas por una distancia r en el vacío está dada por

$F∝q_1q_2\\ F∝\frac{1}{r^2}\\ F=k\frac{q_1q_2}{r^2}\\ F=\frac{q_1q_2}{4\pi{\epsilon}_\circ{r^2}}$

Donde F es la fuerza entre dos cargas puntuales, q ₁ y q ₂ son la carga puntual, r es la distancia entre la carga puntual y k es la constante de proporcionalidad.

Para mayor simplicidad, la constante k en la expresión anterior se escribe comúnmente como

$k=\frac{1}{4\pi{\epsilon}_\circ}$

Aquí, $\epsilon_\circ$ se conoce como la permitividad del espacio libre. El valor de $\epsilon_\circ$ en unidades SI es $\epsilon_\circ=8.854\times10^{-12}\text{ C}^2\text{N}^{-1}\text{m}^{-2}$

Problema 4: ¿Por qué la fuerza de Coulombs actúa entre dos cargas sólo en la línea que une sus centros?

Solución:

Debido a las características fundamentales de la carga eléctrica, este es el caso. Las cargas que son similares se repelen entre sí. Las cargas diametralmente opuestas se atraen.

La fuerza de atracción o repulsión entre dos cargas se dirigirá en la dirección en que la fuerza realice la menor cantidad de trabajo. Como resultado de este requisito, la acción se dirige a lo largo de la línea recta que une las dos cargas, que es la distancia más corta entre ellas.

Problema 5: Compara la naturaleza de las fuerzas electrostática y gravitacional.

Solución:

Entre dos enormes masas, actúa una fuerza gravitacional. Sin embargo, una fuerza electrostática se activa cuando dos cuerpos cargados entran en contacto.

similitudes:

Estas dos fuerzas son fuerzas centrales.

Sigue la ley de los cuadrados inversos.

Ambos son fuerzas de largo alcance.

Ambas fuerzas son naturalmente conservativas.

Disimilitudes:

En la naturaleza, la fuerza electrostática puede ser tanto atractiva como repelente. En la naturaleza, la fuerza gravitacional solo puede ser atractiva.

El medio material entre dos cargas afecta la fuerza eléctrica entre ellas. El medio material entre cuerpos enormes tiene poco efecto sobre la fuerza gravitatoria.

Las fuerzas eléctricas son extremadamente poderosas (aproximadamente 10 38 veces más fuertes) que las fuerzas gravitatorias.

Publicación traducida automáticamente

Artículo escrito por anoopraj758 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Ley de Coulomb

Fórmula de la ley de Coulomb

Ley de Coulomb en forma vectorial

Fuerza entre cargas múltiples

Limitaciones de la Ley de Coulomb

Aplicaciones de la Ley de Coulomb

Problemas de muestra

Deja una respuesta Cancelar la respuesta