Si bien una manzana no pudo haber caído sobre la cabeza de Sir Isaac Newton como dice la historia, lo inspiró a hacer uno de los descubrimientos más importantes de la mecánica: la Ley de la Gravitación Universal . Newton descubrió que la Tierra misma sería responsable del movimiento hacia abajo de la manzana después de reflexionar por qué nunca cae hacia abajo, hacia atrás o en cualquier otra dirección que no sea perpendicular al suelo. Newton pudo formular una ley física general por deducción después de plantear la hipótesis de que esta fuerza sería igual a las masas de las dos fuerzas en cuestión utilizando las observaciones existentes sobre la relación del inverso del cuadrado de la fuerza entre la tierra y la luna. Por lo tanto, analicemos primero esta fuerza gravitacional.
¿Qué es la Fuerza Gravitacional?
La fuerza gravitacional es la fuerza de atracción entre dos cuerpos cualesquiera. Todos los objetos del universo se atraen entre sí con cierta cantidad de fuerza, pero en la mayoría de los casos, la fuerza es demasiado débil para ser observada debido a la gran distancia de separación. Esta fuerza de atracción, también conocida como Fuerza Gravitacional, fue identificada por primera vez por un gran científico llamado Isaac Newton. Este concepto fue desarrollado como Ley Universal de la Gravitación de Newton en el año 1680.
Las propiedades importantes de la fuerza gravitacional son:
- La fuerza gravitatoria es la fuerza más débil de la naturaleza, pero tiene un alcance infinito.
- La fuerza gravitacional siempre es atractiva.
- La fuerza gravitacional actúa entre dos piezas cualesquiera de materia en el Universo ya que la masa es su fuente.
- La fuerza gravitacional es una fuerza central que depende solo de la posición de la masa de prueba de la masa fuente.
- La fuerza gravitacional siempre actúa a lo largo de la línea que une los centros de dos cuerpos.
Algunos ejemplos de la fuerza gravitatoria son:
- Si alguien salta hacia arriba en el cielo, alguien no puede flotar en el aire, vuelve a la tierra debido a la fuerza gravitacional.
- Si se lanza una pelota hacia arriba, alcanza cierta altura y cae hacia abajo debido a la fuerza de la gravedad.
- La fuerza de atracción entre el sol y los planetas del Universo es la Fuerza Gravitacional.
Ley de gravitación de Newton
De acuerdo con la Ley de Gravitación Universal, cada punto de masa del universo atrae a todos los demás puntos de masa del universo mediante una fuerza que apunta en línea recta entre sus centros de masa, y esta fuerza es igual a las masas de las partículas y inversamente proporcional a su diferencia. De un punto al siguiente, esta fuerza de atracción a menudo apunta hacia adentro.
Esta ley se aplica a todos los objetos con peso, sin importar cuán grandes o pequeños sean. Si la diferencia entre dos objetos masivos es muy grande en comparación con sus tamaños o si son esféricamente simétricos, se les puede llamar masas puntuales . En estos casos, la masa de cada objeto puede medirse por una masa puntual en su centro de masa.

Representación de dos masas para la Ley de Gravitación de Newton
Por lo tanto, de acuerdo con la ley de gravitación de Newton, cada partícula en el universo atrae a todas las demás partículas con una fuerza cuya magnitud es,
- Directamente proporcional al producto de sus masas, es decir
F ∝ (m 1 × m 2 ) ……(1)
- Inversamente proporcional al cuadrado de la distancia entre sus centros (también conocida como ley del cuadrado inverso), es decir
F ∝ (1 / r 2 ) ……(2)
Al combinar las ecuaciones (1) y (2) se obtiene que,
F ∝ (m 1 × m 2 ) / r 2 ……(3)
Por lo tanto, de la ecuación (3), se puede decir que la fuerza de gravedad o fuerza de gravedad entre dos partículas u objetos es proporcional al producto de sus masas por el cuadrado de la distancia que los separa.
F = G × (m 1 × m 2 ) / r 2 ……(4)
Aquí G es la constante de proporcionalidad, también conocida como constante gravitacional, que siempre es una constante universal,
F es la fuerza de gravedad,
m 1 es la masa de un objeto,
m 2 es la masa del otro objeto y
r es la distancia entre esos objetos.
¿Qué es la constante gravitatoria?
La constante gravitatoria es una constante de proporcionalidad y se utiliza en la Ley de gravitación universal de Newton. Se denota por G.
También se puede definir como una fuerza de atracción entre dos unidades de masa separadas por una unidad de distancia. De la Ley de Gravitación Universal de Newton, es decir, de la ecuación (4), la expresión para G es:
F = GRAMO × (m 1 × m 2 ) / r 2
GRAMO = F × r 2 / (m 1 × m 2 )
Cuando r = 1 m y m 1 = m 2 = 1 kg. después
sol = F
La fórmula dimensional para G es [M -1 L 3 T -2 ].
Sus valores en unidades SI es 6,67 × 10 -11 Nm 2 kg -2 y en sistema CGS es 6,67 × 10 -8 dina cm 2 g -2 .
Importancia de la Ley Gravitacional
La ley universal de la Gravitación explicó con éxito muchos conceptos como:
- ¿Cómo se produce el movimiento planetario?
- ¿Cómo se afectan entre sí todos los objetos del Universo?
- ¿Cómo se produce el movimiento lunar alrededor de la tierra?
- ¿Cómo nos mantenemos siempre en el suelo y cómo la gravedad es la responsable del peso del cuerpo?
Forma vectorial de la ley de gravitación de Newton
El par acción-reacción formado por las fuerzas gravitatorias que actúan entre las dos partículas se denomina forma vectorial de la ley de gravitación de Newton. Considere dos cuerpos de masa puntuales A y B de masas m₁ y m₂ colocados a una distancia r, como se muestra en la siguiente figura:

Aquí ![]()
![]()
![]()
![]()

De la figura anterior, se puede ver que las dos partículas de masas y se colocan a una distancia
![]()
Por lo tanto, según la ley de gravitación de Newton, la fuerza aplicada sobre m 2 por m 1 es

El signo negativo indica la naturaleza atractiva de la fuerza.
Del mismo modo, la fuerza gravitatoria sobre m 1 por m 2
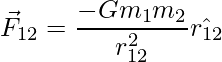
Lo sabemos ![]()
⇒ | r 12 | 2 = | r 21 | 2
Así, se obtiene que:
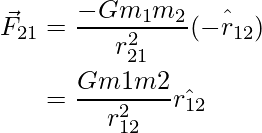
![]()
Esto implica que los dos vectores anteriores son iguales y opuestos entre sí, lo que indica que la fuerza gravitacional satisface la tercera ley de Newton.
Por lo tanto, esta forma vectorial de la ley de gravitación de Newton significa que las fuerzas gravitatorias que actúan entre las dos partículas forman el par acción-reacción como se muestra arriba.
Principio de Superposición de Fuerzas Gravitatorias
El principio de la superposición de fuerzas gravitatorias establece que la fuerza gravitatoria total sobre cualquier objeto es igual a la suma de las fuerzas gravitatorias individuales que actúan sobre ese objeto. En otras palabras, el campo gravitacional neto en un punto es la suma vectorial de los campos gravitatorios en ese punto debido a diferentes fuentes y se expresa como:
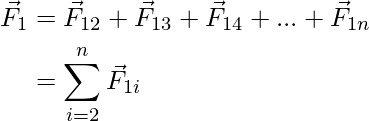
donde ![]() es la fuerza gravitacional total sobre un objeto, ,
es la fuerza gravitacional total sobre un objeto, , ![]() y son fuerzas independientes que actúan por separado sobre ese objeto.
y son fuerzas independientes que actúan por separado sobre ese objeto.![]()
![]()
![]()
Deducción de la Ley de Gravitación de Newton a partir de la Ley de Kepler
Supongamos que un planeta de masa m gira alrededor del sol de masa M en una órbita casi circular de radio r, con una velocidad angular constante ω. Sea T el período de tiempo de revolución del planeta alrededor del sol.
Por lo tanto,
F = mrω 2
= señor × (2π/T) 2 ……(1)
De acuerdo con la tercera ley de Kepler, el cuadrado del período de tiempo del planeta es proporcional a los cuadrados de la longitud de los ejes semi-mayores y se da como:
T 2 ∝ r 3
o
T 2 = kr 3
donde k es la constante de proporcionalidad, T es el período de tiempo del planeta y r es la longitud del semieje mayor.
Ahora aplique esto en la ecuación (1) como:
F = señor × (4π 2 / kr 3 )
= (4π 2 × m) / kr 2
Pero k = 4π 2 / GM, sustituya esto en la expresión anterior como:
F = (G × M × m) / r 2
que es la ecuación de la ley de gravitación de Newton.
Por lo tanto, Newton dedujo lo siguiente de las Leyes de Kepler:
- Una fuerza que se produce en la tierra debido al sol es la fuerza centrípeta, que está orientada hacia el sol.
- La gravedad del planeta debe ser inversamente proporcional al cuadrado de su distancia al sol.
- La fuerza que actúa sobre la tierra es proporcional al producto de las masas de la tierra y del sol.
Ejemplos de problemas sobre la ley de gravitación de Newton
Problema 1: ¿Será diferente la fuerza de atracción gravitatoria si se llevan los mismos cuerpos a la Luna manteniendo constante su distancia de separación?
Solución:
Si se llevan los mismos cuerpos a la luna manteniendo constante su distancia de separación, entonces la fuerza de atracción gravitacional entre los dos cuerpos permanece igual, ya que la fuerza de atracción gravitatoria entre dos cuerpos no se ve afectada por la presencia del tercer cuerpo y el medio entre ellos. los dos cuerpos.
Por lo tanto, la fuerza de atracción gravitatoria sigue siendo la misma entre esos cuerpos después de llegar a la luna.
Problema 2: Dos cuerpos de masas 5 kg y 6 kg se colocan con sus centros separados 64 m. Calcular la aceleración inicial de dos masas suponiendo que no actúen otras fuerzas sobre ellas.
Solución:
Dado que,
La masa del primer cuerpo, m 1 es de 5 kg.
La masa del segundo cuerpo, m 2 es de 6 kg.
La distancia entre los dos cuerpos, r es de 64 m.
Y el valor de la constante gravitatoria universal, G es 6,67 × 10 -11 Nm 2 kg -2
Por la ley de gravitación de Newton, la fórmula para la fuerza gravitacional se da como
F = GRAMO × (m 1 × m 2 ) / r 2
Sustituya los valores dados en la expresión anterior como:
F = 6,67 × 10 -11 Nm 2 kg -2 × (5 kg × 6 kg) / (64 m) 2
= 48,85 × 10 -14 N
Ahora, se sabe que, la fuerza neta sobre un objeto está dada por:
F = mamá
o
a = F/m
Sustituya los valores dados y obtenidos en la expresión anterior para calcular a para dos cuerpos como:
a 1 = 48,85 × 10 -14 N / 5 kg
= 9,77 × 10 -14 m/s 2
Y
a 2 = 48,85 × 10 -14 N / 6 kg
= 8,142 × 10 -14 m/s 2
Así, las aceleraciones iniciales de dos cuerpos son 9,77 × 10 -14 m/s 2 y 8,142 × 10 -14 m/s 2 respectivamente.
Problema 3: Un cuerpo de 1 kg de masa y otro cuerpo de 10 kg de masa están separados por una distancia de 100 m, y son atraídos por una fuerza de 19.6×10 -10 N. Calcula el valor de la constante de gravitación universal para el caso dado.
Solución:
Dado que,
La masa del primer cuerpo, m 1 es 1 kg.
La masa del segundo cuerpo, m 2 es de 10 kg.
La distancia entre los dos cuerpos, r es de 100 m.
La fuerza de atracción gravitatoria entre los dos cuerpos F es 19,6 × 10 -10 N.
Por lo tanto, de la ley de la Gravitación de Newton:
GRAMO = F × r 2 / (m 1 × m 2 )
= 19,6 × 10 -10 N × (100 m) 2 / (1 kg × 100 kg)
= 19,6 × 10 -7 Nm 2 kg -2
Así, el valor de la constante de gravitación universal para este caso es 19,6 × 10 -7 Nm 2 kg -2 .
Problema 4: Si los dos objetos se atraen con una fuerza gravitacional de F unidades. Si la masa de ambos objetos se triplicó y la distancia entre los objetos también se duplicó. ¿Cuál sería la nueva fuerza de atracción entre dos objetos?
Solución:
Sea F N la fuerza de atracción entre dos cuerpos.
Y se sabe por la ley de gravitación de Newton que la fuerza de atracción gravitatoria es,
F = GRAMO × (m 1 × m 2 ) / r 2
donde m 1 es la masa del primer objeto, m 2 es la masa del segundo objeto y r es la distancia entre los dos cuerpos.
Sea F 1 la nueva fuerza de atracción entre dos objetos.
Cuando la masa de ambos objetos se triplica y la distancia entre los objetos se duplica, entonces la fuerza que actúa entre dos objetos es,
F 1 = sol × (3 × metro 1 × 3 × metro 2 ) / (2r) 2
= 9G × metro 1 × metro 2 / 4r 2
= 9F / 4
Así, la nueva fuerza de atracción entre dos objetos es 9F/4 unidades.
Problema 5: Calcular la fuerza resultante que actúa sobre la masa m que está en la posición 1 y todas las masas que son iguales a m están colocadas en los vértices del triángulo equilátero que tiene la longitud de su lado r.
Solución:
Dado eso, las masas cuyo peso es igual a m se colocan en las tres esquinas del triángulo equilátero.
Sea F 1 la fuerza que actúa sobre la masa m que está en la posición 1.
Por el Principio de Superposición de Fuerzas Gravitatorias,
F 1 = fuerzas que actúan sobre la masa m debido a otra masa m que está en la posición 2 + fuerzas que actúan sobre la masa m debido a otra masa m que está en la posición 3.
Aquí
y
forman un ángulo de 60° entre sí ya que actúan a lo largo de los lados del triángulo equilátero.
Dejar
F res =
=
F res =√3f=√3×Gm 2 /r 2
Así, la fuerza resultante que actúa sobre la masa m que está en la posición 1 y todas las masas que son iguales a m están colocadas en los vértices del triángulo equilátero que tiene la longitud de su lado es √3Gm 2 /r 2 .
Problema 6: Tres esferas uniformes, cada una con una masa M y un radio a, se mantienen de tal manera que cada una toque a las otras dos. Encuentre la magnitud de la fuerza gravitacional sobre cualquiera de las esferas debido a las otras dos esferas.
Solución:
Sean A, B y C los centros de tres esferas uniformes.
Sea
la fuerza que actúa sobre C debido a A y
sea la fuerza que actúa sobre C debido a B
Sea la fuerza total que actúa sobre C debido a A y B
Por el Principio de Superposición de Fuerzas Gravitatorias,
⇒
……(1)
Al unir A, B y C, obtenemos un triángulo equilátero, es decir, forma un ángulo de 60° entre sí.
Dado el radio de cada esfera es un
entonces AB=BC=CA=2a
De la ley de la gravitación de Newton,
Aquí
De 1),
=
=
|F| =
Por tanto, la magnitud de la fuerza gravitatoria sobre cualquiera de las esferas debida a las otras dos esferas es
Problema 7: Si Mercurio, Venus y el Sol están alineados en un triángulo rectángulo. Calcule la suma vectorial de las fuerzas sobre Venus debidas tanto a Mercurio como al Sol. ¿Cuál es la dirección y la magnitud de la fuerza resultante?
Solución:
Dado que,
Distancia entre el Sol y Venus (r v) =108×10 9 metros.
Distancia entre el Sol y Mercurio (r m) = 57,6 × 10 9 metros
Distancia entre Mercurio y Venus (r mv )=
⇒ r mv =1,08×10 11 metros.
Masa del Sol= 1.99×10 30 kg
Masa de Mercurio =3.3×10 23 kg
Masa de Venus = 4,87 × 10 24 kg
Deje que la fuerza que actúa sobre Venus debido al Sol sea F S
De la ley de la gravitación de Newton,
= 6.67×10 -11 ×1.99×10 30 ×4.87×10 24 /(108×10 9 )^2
FS = 5,54 × 10 22 N
Sea la fuerza que actúa sobre Venus debido a Mercurio F M
⇒
= 6,67×10 -11 ×3,3×10 23 ×4,87×10 24 /(1,08 ×10 11 ) 2
F M = 9.19×10 15 N
Aquí, la Fuerza debida al Sol es más de un millón de veces mayor que la Fuerza debida a Mercurio, por lo que la Fuerza neta se debe principalmente al Sol y su magnitud es igual a la Fuerza que actúa debida al Sol. Y la dirección de la Fuerza resultante similar a la dirección debida al Sol.
Publicación traducida automáticamente
Artículo escrito por prasanthinidamarthy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA



