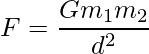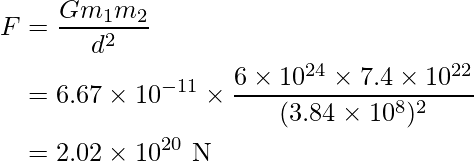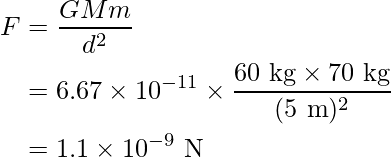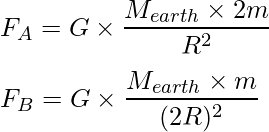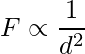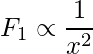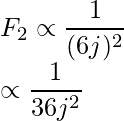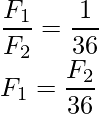Ya sea que esa manzana realmente haya aterrizado en la cabeza de Isaac Newton o no, como dicen algunas historias, esta ecuación dada por la ley universal de la gravitación describe por qué todos permanecen enraizados en el suelo, qué bloquea a la Tierra en órbita alrededor del sol y para enviar a los hombres a la Luna. Resume la idea de que todas las partículas de materia en el universo se atraen entre sí a través de la fuerza de la gravedad, la ley de Newton dice qué tan fuerte es esa atracción. Analicemos cómo esta ley salió a la luz y se derivó.
¿Qué es la gravitación?
La gravitación es una fuerza que establece que todos los objetos en la tierra o en el espacio se atraen entre sí. La fuerza gravitatoria sobre el objeto depende de la masa del objeto, cuanto mayor sea la masa del objeto, mayor será la fuerza que le apliquen los otros objetos. Todos los objetos que podemos ver se atraen entre sí en cierta medida, como un bolígrafo, un borrador, planetas, un teléfono móvil, un reloj o una nevera. La fuerza gravitacional es una de las fuerzas sin contacto con la fuerza electromagnética y la fuerza nuclear.

La Tierra gira en su órbita alrededor del sol atraída por la gravedad del sol.
Ley Universal de la Gravitación
Cada objeto en el universo atrae a todos los demás objetos por una fuerza que es directamente proporcional al producto de las masas de ambos objetos e inversamente proporcional al cuadrado de la distancia entre ellos. Esto se conoce como Ley Universal de la Gravitación. Esto tiene una historia muy interesante y mucho trabajo manual e investigación de muchos científicos y matemáticos.
Un día, Isaac Newton estaba sentado bajo un manzano en su universidad. Una manzana cayó en la tierra, y él pensó por qué esta manzana cayó, por qué esta no subió. Esta curiosidad lo golpeó con fuerza, y comenzó a trabajar en ello y a encontrar una solución matemática para que la manzana se cayera. Dio una ley para esto, llamada “La Ley Universal de la Gravitación” .

Representación para la Ley Universal de la Gravitación
De acuerdo con la ley de gravitación universal de Newton, la fuerza gravitatoria que existe entre las dos masas, digamos m 1 y m 2 , es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre las dos masas ie
Matemáticamente, ambas condiciones se pueden interpretar como:
- F ∝ metro 1 × metro 2
- F ∝ 1 / re 2
Combinando las dos condiciones anteriores, se obtiene como:
- F ∝ metro 1 × metro 2 / re 2
Ahora, deduciendo la condición anterior a una ecuación. Eliminar el signo de proporcionalidad introduciendo la constante de proporcionalidad.
Aquí, G es la constante de proporcionalidad y se conoce como la constante gravitatoria igual a 6,67 × 10 −11 N⋅m 2 / kg 2 .
Importancia de la Ley Universal de la Gravitación
Esta ley universal de la Gravitación abrió muchos caminos para más investigación y para encontrar el funcionamiento de nuestro universo con la existencia de organismos vivos en los planetas. La nave espacial usa esta ecuación para calcular diferentes resultados. La gravedad es muy importante para nosotros. Nos mantiene en la órbita para girar alrededor del Sol y obtener la luz del sol y el calor. La gravedad también retiene el aire y la atmósfera terrestre. Los agujeros negros son el lugar donde se puede ver el poder de la fuerza gravitacional. Los agujeros negros engullen todo, incluso la luz, y almacenan todo en un lugar muy pequeño en su cola llamado Singularidad.
La fuerza que nos une a la Tierra:
Todas las cosas vivas y no vivas están en la tierra, no dejan la atmósfera terrestre y caen al espacio exterior. Aunque los humanos han desarrollado algunas tecnologías para penetrar esta fuerza y salir al espacio para la exploración. La gravedad es la fuerza que nos trae de vuelta a la tierra cuando saltamos.

Fuerza sobre nosotros por la Tierra
El movimiento de la Luna alrededor de la Tierra:
La teoría del impacto gigante dice que la luna era parte de la tierra y durante las primeras fases de la creación de la tierra se desprendió y comenzó a girar alrededor de la tierra debido a la fuerza gravitacional de la luna. El tiempo de revolución y el tiempo de rotación de la Luna son iguales, por eso solo podemos ver un lado.

El movimiento de los planetas alrededor del sol:
Durante mucho tiempo, la gente solía creer que el sol giraba alrededor del sol. Cuando Galileo Galilei dijo que la tierra giraba alrededor del Sol, se le ordenó venir al Santo Oficio para el juicio, y será encarcelado y permanecerá en soledad. Incluso el Sol también orbita alrededor de la Vía Láctea. Se necesitan 236 millones de años para completar una órbita. Nuestra galaxia es una vasta área de investigación.

Movimiento de los planetas alrededor del sol
Problemas de muestra
Problema 1: La masa de la tierra es 6 × 10 24 kg y la de la luna es 7,4 × 10 22 kg. Si la distancia entre la tierra y la luna es de 3,84 × 10 5 km, calcula la fuerza que ejerce la tierra sobre la luna.
Solución:
Dado que,
La masa de la tierra, m 1 es 6 × 10 24 kg.
La masa de la luna, m 2 es 7,4 × 10 22 kg.
La distancia entre la tierra y la luna, d es 3.84 × 10 5 km.
La fórmula para calcular la fuerza que ejerce la tierra sobre la luna es:
Por tanto, la fuerza ejercida por la tierra sobre la luna es igual a 2,02 × 10 20 N.
Problema 2: Tu profesor te está enseñando la ley de la gravitación a 5 m de ti, si su masa es de 60 kg, ¿cuál es el valor de la fuerza gravitatoria que ejerces sobre él? (Sugerencia: tome su peso usted mismo).
Solución:
Dado que,
La masa del maestro, M es de 60 kg.
La masa de la persona, m es de 70 kg.
La distancia entre ellos, d es de 5 m.
La fórmula para calcular la fuerza gravitatoria que ejerce la persona sobre el profesor es:
Por tanto, la fuerza gravitatoria que ejerce la persona sobre el profesor es de 1,1 × 10 -9 N.
Problema 3: Un satélite A tiene el doble de masa que el satélite B. El satélite A orbita el planeta con la mitad del radio del satélite B. ¿Cuántas veces la fuerza sobre el satélite A en comparación con el satélite B por la tierra?
Solución:
Considere la masa del satélite B como m y la masa del satélite A como 2m.
Ahora, para calcular la fuerza gravitacional para ambos satélites, divida ambas fuerzas para obtener una ecuación como:
Ahora divida la fuerza sobre A por la Fuerza sobre B como:

Satélites que orbitan la tierra
Por lo tanto, la fuerza sobre el satélite A es 8 veces la fuerza sobre el satélite B.
Problema 4: La ley de gravitación de Newton se aplica a:
una. Solo cuerpos pequeños
b. Solo plantas
C. Todos los cuerpos independientemente de su tamaño.
d. para sistema solar
Solución:
La ley de gravitación de Newton es aplicable a todos los cuerpos independientemente de su tamaño.
Por lo tanto, la Opción c. es correcto.
Problema 5: Considere dos cuerpos en contacto tales que la distancia entre ellos es seis veces mayor que la distancia habitual. Calcula cuánto cambió la fuerza.
Solución:
Según la ley universal de Newton, la fuerza gravitacional (F) es inversamente proporcional al cuadrado de la distancia (d) entre los dos objetos en contacto.
Matemáticamente:
Considere que la distancia habitual entre los dos cuerpos sea x.
Entonces, la fuerza inicial se da como:
Ahora, cuando la distancia entre los dos cuerpos cambió a 6x, la nueva fuerza se da como:
Ahora, divide las dos fuerzas como:
Por lo tanto, la fuerza habitual cambia 1/36 veces la nueva fuerza.
Publicación traducida automáticamente
Artículo escrito por hemusharma196 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA