Longitud del subsegmento más largo que es UpDown después de insertar al menos un entero

Se dice que una secuencia de enteros $(a_1, a_2, ..., a_k)$ es UpDown, si la desigualdad $a_1 \leq a_2 \geq a_3 \leq a_4 \geq a_5 ...$ se cumple.
Se le da una secuencia $(s_1, s_2, s_3, ..., s_n)$ . Puede insertar como máximo un entero en la secuencia. Podría ser cualquier número entero. Encuentre la longitud del subsegmento más largo de la nueva secuencia después de agregar un número entero (o elegir no hacerlo) que es UpDown.
Un subsegmento es una parte consecutiva de una secuencia. Es decir, un subsegmento de $(b_1, b_2, ..., b_k)$ será de la forma $(b_i, b_{i+1}, b_{i+2}, ..., b_j)$ para algunos $i$ y $j$ .
Este problema fue planteado en la Olimpiada de Computación Zonal 2019 .
Ejemplos:

Entrada: arr[] = {1, 10, 3, 20, 25, 24}
Salida: 7
Supongamos que insertamos 5 entre 20 y 25, la secuencia completa (1, 10, 3, 20, 5, 25, 24)
se convierte en una secuencia UpDown y, por lo tanto, la respuesta es 7.
Entrada: arr[] = {100, 1, 10, 3, 4, 6, 11}
Salida: 6
Supongamos que insertamos 4 entre 4 y 6, la secuencia (1, 10, 3, 4, 4, 6) se convierte en una
Secuencia UpDown y por lo tanto la respuesta es 6. Podemos verificar que esta es la mejor
solución posible.

Enfoque: Comencemos definiendo dos tipos de secuencia:-

UpDown Sequence (UD): una secuencia de la forma 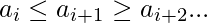$a_{i} \leq a_{i+1} \geq a_{i+2} ...$ Es decir, la secuencia comienza aumentando primero.
DownUp Sequence (DU): una secuencia de la forma 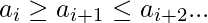$a_{i} \geq a_{i+1} \leq a_{i+2} ...$ Es decir, la secuencia comienza decreciendo primero.

Averigüemos primero la longitud de las secuencias UD y DU sin pensar en otras partes del problema. Para eso, definamos $f(idx, 1)$ que es la secuencia UpDown más larga que comienza en $idx$ y $f(idx, 2)$ que es la secuencia DownUp más larga que comienza en $idx$ .
La relación de recurrencia para $f$ es: –

$\begin{equation*} f(idx, state)=\begin{cases} 1, idx = N\\ 1, \text{$state = 1 \ and \ s_i > s_{i+1}$}\\ 1, \text{$state = 2 \ and \ s_{i+1} > s_i$}\\ 1 + f(idx+1, 2), \text{$state=1 \ and \ s_i \leq \ s_{i+1}$}\\ 1 + f(idx+1, 1), \text{$state=2 \ and \ s_{i+1} \leq \ s_i$}\\ \end{cases} \end{equation*}$

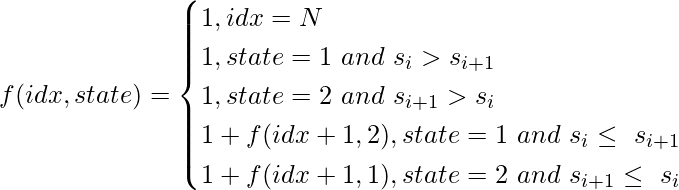
Aquí, N es la longitud de la secuencia y el estado es 1 o 2 y representa la secuencia UD y DU respectivamente. Al formar la relación de recurrencia, usamos el hecho de que en una secuencia UD

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

, la parte

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

es una secuencia DU y viceversa . Podemos usar la programación dinámica para calcular el valor de $f$ y luego almacenar nuestro resultado en la array dp[N][2] .
Ahora, observe que siempre es posible insertar un número entero al final de una secuencia UpDown para aumentar la longitud de la secuencia en 1 y, sin embargo, conservar la desigualdad UpDown. Por qué ? Supongamos que una secuencia UD se rompe en $a_k$ el momento $a_k > a_{k+1}$ en que esperábamos que fuera $a_k \leq a_{k+1}$ . Podemos insertar un número entero $x = a_k$ entre $a_k$ y $a_{k+1}$ . Ahora, $a_k \leq x \geq a_{k+1}$ está satisfecho.
Podemos dar un argumento similar para el caso cuando la secuencia UD se rompe $a_k$ porque $a_k > a_{k+1}$ cuando esperábamos que fuera $a_k \leq a_{k+1}$ . Pero en realidad no tenemos que insertar nada. Solo tenemos que encontrar la longitud de la secuencia UD más larga posible.
Observe que una secuencia UD es una combinación de: –

Secuencia UD I + x + Secuencia UD II si la longitud de la secuencia UD I es impar
Secuencia UD I + x + Secuencia UD I si la longitud de la secuencia UD I es par

donde, x es el elemento insertado.
Entonces, para cada i, calculamos la longitud de la secuencia UD más larga que comienza en i. Sea esa longitud y.
Si y es impar, insertamos un elemento allí (teóricamente) y calculamos la longitud de la secuencia UD más larga que comienza en i+y. La secuencia UD más larga que comienza en i después de insertar un elemento es, por lo tanto, dp[i][1] + 1 + dp[i+y][1] .
Si y es par, insertamos un elemento allí (teóricamente) y calculamos la longitud de la secuencia DU más larga que comienza en i+y. La secuencia UD más larga que comienza en i después de insertar un elemento es, por lo tanto, dp[i][1] + 1 + dp[i+y][2] .
La respuesta final es el máximo de dicho valor entre todos los i.

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to recursively fill the dp array
int f(int i, int state, int A[], int dp[][3], int N)
{
    if (i >= N)
        return 0;
 
    // If f(i, state) is already calculated
    // then return the value
    else if (dp[i][state] != -1) {
        return dp[i][state];
    }
 
    // Calculate f(i, state) according to the
    // recurrence relation and store in dp[][]
    else {
        if (i == N - 1)
            dp[i][state] = 1;
        else if (state == 1 && A[i] > A[i + 1])
            dp[i][state] = 1;
        else if (state == 2 && A[i] < A[i + 1])
            dp[i][state] = 1;
        else if (state == 1 && A[i] <= A[i + 1])
            dp[i][state] = 1 + f(i + 1, 2, A, dp, N);
        else if (state == 2 && A[i] >= A[i + 1])
            dp[i][state] = 1 + f(i + 1, 1, A, dp, N);
        return dp[i][state];
    }
}
 
// Function that calls the resucrsive function to
// fill the dp array and then returns the result
int maxLenSeq(int A[], int N)
{
    int i, tmp, y, ans;
 
    // dp[][] array for storing result
    // of f(i, 1) and f(1, 2)
    int dp[1000][3];
 
    // Populating the array dp[] with -1
    memset(dp, -1, sizeof dp);
 
    // Make sure that longest UD and DU
    // sequence starting at each
    // index is calculated
    for (i = 0; i < N; i++) {
        tmp = f(i, 1, A, dp, N);
        tmp = f(i, 2, A, dp, N);
    }
 
    // Assume the answer to be -1
    // This value will only increase
    ans = -1;
    for (i = 0; i < N; i++) {
 
        // y is the length of the longest
        // UD sequence starting at i
        y = dp[i][1];
 
        if (i + y >= N)
            ans = max(ans, dp[i][1] + 1);
 
        // If length is even then add an integer
        // and then a DU sequence starting at i + y
        else if (y % 2 == 0) {
            ans = max(ans, dp[i][1] + 1 + dp[i + y][2]);
        }
 
        // If length is odd then add an integer
        // and then a UD sequence starting at i + y
        else if (y % 2 == 1) {
            ans = max(ans, dp[i][1] + 1 + dp[i + y][1]);
        }
    }
    return ans;
}
 
// Driver code
int main()
{
    int A[] = { 1, 10, 3, 20, 25, 24 };
    int n = sizeof(A) / sizeof(int);
 
    cout << maxLenSeq(A, n);
 
    return 0;
}

Java

// Java implementation of the approach
class GFG
{
     
    // Function to recursively fill the dp array
    static int f(int i, int state, int A[],
                 int dp[][], int N)
    {
        if (i >= N)
            return 0;
     
        // If f(i, state) is already calculated
        // then return the value
        else if (dp[i][state] != -1)
        {
            return dp[i][state];
        }
     
        // Calculate f(i, state) according to the
        // recurrence relation and store in dp[][]
        else
        {
            if (i == N - 1)
                dp[i][state] = 1;
            else if (state == 1 && A[i] > A[i + 1])
                dp[i][state] = 1;
            else if (state == 2 && A[i] < A[i + 1])
                dp[i][state] = 1;
            else if (state == 1 && A[i] <= A[i + 1])
                dp[i][state] = 1 + f(i + 1, 2, A, dp, N);
            else if (state == 2 && A[i] >= A[i + 1])
                dp[i][state] = 1 + f(i + 1, 1, A, dp, N);
            return dp[i][state];
        }
    }
     
    // Function that calls the resucrsive function to
    // fill the dp array and then returns the result
    static int maxLenSeq(int A[], int N)
    {
        int i,j, tmp, y, ans;
     
        // dp[][] array for storing result
        // of f(i, 1) and f(1, 2)
        int dp[][] = new int[1000][3];
         
        // Populating the array dp[] with -1
        for(i= 0; i < 1000; i++)
            for(j = 0; j < 3; j++)
                dp[i][j] = -1;
 
        // Make sure that longest UD and DU
        // sequence starting at each
        // index is calculated
        for (i = 0; i < N; i++)
        {
            tmp = f(i, 1, A, dp, N);
            tmp = f(i, 2, A, dp, N);
        }
     
        // Assume the answer to be -1
        // This value will only increase
        ans = -1;
        for (i = 0; i < N; i++)
        {
     
            // y is the length of the longest
            // UD sequence starting at i
            y = dp[i][1];
     
            if (i + y >= N)
                ans = Math.max(ans, dp[i][1] + 1);
     
            // If length is even then add an integer
            // and then a DU sequence starting at i + y
            else if (y % 2 == 0)
            {
                ans = Math.max(ans, dp[i][1] + 1 + dp[i + y][2]);
            }
     
            // If length is odd then add an integer
            // and then a UD sequence starting at i + y
            else if (y % 2 == 1)
            {
                ans = Math.max(ans, dp[i][1] + 1 + dp[i + y][1]);
            }
        }
        return ans;
    }
     
    // Driver code
    public static void main (String[] args)
    {
        int A[] = { 1, 10, 3, 20, 25, 24 };
        int n = A.length;
     
        System.out.println(maxLenSeq(A, n));
    }
}
 
// This code is contributed by AnkitRai01

Python3

# Python3 implementation of the approach
 
# Function to recursively fill the dp array
def f(i, state, A, dp, N):
    if i >= N:
        return 0
 
    # If f(i, state) is already calculated
    # then return the value
    elif dp[i][state] != -1:
        return dp[i][state]
 
    # Calculate f(i, state) according to the
    # recurrence relation and store in dp[][]
    else:
        if i == N - 1:
            dp[i][state] = 1
        elif state == 1 and A[i] > A[i + 1]:
            dp[i][state] = 1
        elif state == 2 and A[i] < A[i + 1]:
            dp[i][state] = 1
        elif state == 1 and A[i] <= A[i + 1]:
            dp[i][state] = 1 + f(i + 1, 2, A, dp, N)
        elif state == 2 and A[i] >= A[i + 1]:
            dp[i][state] = 1 + f(i + 1, 1, A, dp, N)
 
        return dp[i][state]
 
# Function that calls the resucrsive function to
# fill the dp array and then returns the result
def maxLenSeq(A, N):
 
    # dp[][] array for storing result
    # of f(i, 1) and f(1, 2)
    # Populating the array dp[] with -1
    dp = [[-1, -1, -1] for i in range(1000)]
 
    # Make sure that longest UD and DU
    # sequence starting at each
    # index is calculated
    for i in range(N):
        tmp = f(i, 1, A, dp, N)
        tmp = f(i, 2, A, dp, N)
 
    # Assume the answer to be -1
    # This value will only increase
    ans = -1
    for i in range(N):
 
        # y is the length of the longest
        # UD sequence starting at i
        y = dp[i][1]
        if (i + y) >= N:
            ans = max(ans, dp[i][1] + 1)
 
        # If length is even then add an integer
        # and then a DU sequence starting at i + y
        elif y % 2 == 0:
            ans = max(ans, dp[i][1] + 1 + dp[i + y][2])
 
        # If length is odd then add an integer
        # and then a UD sequence starting at i + y
        elif y % 2 == 1:
            ans = max(ans, dp[i][1] + 1 + dp[i + y][1])
 
    return ans
 
# Driver Code
if __name__ == "__main__":
    A = [1, 10, 3, 20, 25, 24]
    n = len(A)
    print(maxLenSeq(A, n))
 
# This code is contributed by
# sanjeev2552

C#

// C# implementation of the approach
using System;
     
class GFG
{
     
    // Function to recursively fill the dp array
    static int f(int i, int state, int []A,
                 int [,]dp, int N)
    {
        if (i >= N)
            return 0;
     
        // If f(i, state) is already calculated
        // then return the value
        else if (dp[i, state] != -1)
        {
            return dp[i, state];
        }
     
        // Calculate f(i, state) according to the
        // recurrence relation and store in dp[,]
        else
        {
            if (i == N - 1)
                dp[i, state] = 1;
            else if (state == 1 && A[i] > A[i + 1])
                dp[i, state] = 1;
            else if (state == 2 && A[i] < A[i + 1])
                dp[i, state] = 1;
            else if (state == 1 && A[i] <= A[i + 1])
                dp[i, state] = 1 + f(i + 1, 2, A, dp, N);
            else if (state == 2 && A[i] >= A[i + 1])
                dp[i, state] = 1 + f(i + 1, 1, A, dp, N);
            return dp[i, state];
        }
    }
     
    // Function that calls the resucrsive function to
    // fill the dp array and then returns the result
    static int maxLenSeq(int []A, int N)
    {
        int i, j, tmp, y, ans;
     
        // dp[,] array for storing result
        // of f(i, 1) and f(1, 2)
        int [,]dp = new int[1000, 3];
         
        // Populating the array dp[] with -1
        for(i = 0; i < 1000; i++)
            for(j = 0; j < 3; j++)
                dp[i, j] = -1;
 
        // Make sure that longest UD and DU
        // sequence starting at each
        // index is calculated
        for (i = 0; i < N; i++)
        {
            tmp = f(i, 1, A, dp, N);
            tmp = f(i, 2, A, dp, N);
        }
     
        // Assume the answer to be -1
        // This value will only increase
        ans = -1;
        for (i = 0; i < N; i++)
        {
     
            // y is the length of the longest
            // UD sequence starting at i
            y = dp[i, 1];
     
            if (i + y >= N)
                ans = Math.Max(ans, dp[i, 1] + 1);
     
            // If length is even then add an integer
            // and then a DU sequence starting at i + y
            else if (y % 2 == 0)
            {
                ans = Math.Max(ans, dp[i, 1] + 1 +
                                    dp[i + y, 2]);
            }
     
            // If length is odd then add an integer
            // and then a UD sequence starting at i + y
            else if (y % 2 == 1)
            {
                ans = Math.Max(ans, dp[i, 1] + 1 +
                                    dp[i + y, 1]);
            }
        }
        return ans;
    }
     
    // Driver code
    public static void Main (String[] args)
    {
        int []A = { 1, 10, 3, 20, 25, 24 };
        int n = A.Length;
     
        Console.WriteLine(maxLenSeq(A, n));
    }
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
    // Javascript implementation of the approach
     
    // Function to recursively fill the dp array
    function f(i, state, A, dp, N)
    {
        if (i >= N)
            return 0;
      
        // If f(i, state) is already calculated
        // then return the value
        else if (dp[i][state] != -1)
        {
            return dp[i][state];
        }
      
        // Calculate f(i, state) according to the
        // recurrence relation and store in dp[][]
        else
        {
            if (i == N - 1)
                dp[i][state] = 1;
            else if (state == 1 && A[i] > A[i + 1])
                dp[i][state] = 1;
            else if (state == 2 && A[i] < A[i + 1])
                dp[i][state] = 1;
            else if (state == 1 && A[i] <= A[i + 1])
                dp[i][state] = 1 + f(i + 1, 2, A, dp, N);
            else if (state == 2 && A[i] >= A[i + 1])
                dp[i][state] = 1 + f(i + 1, 1, A, dp, N);
            return dp[i][state];
        }
    }
      
    // Function that calls the resucrsive function to
    // fill the dp array and then returns the result
    function maxLenSeq(A, N)
    {
        let i,j, tmp, y, ans;
      
        // dp[][] array for storing result
        // of f(i, 1) and f(1, 2)
        let dp = new Array(1000);
          
        // Populating the array dp[] with -1
        for(i= 0; i < 1000; i++)
        {
            dp[i] = new Array(3);
            for(j = 0; j < 3; j++)
            {
                dp[i][j] = -1;
            }
        }
  
        // Make sure that longest UD and DU
        // sequence starting at each
        // index is calculated
        for (i = 0; i < N; i++)
        {
            tmp = f(i, 1, A, dp, N);
            tmp = f(i, 2, A, dp, N);
        }
      
        // Assume the answer to be -1
        // This value will only increase
        ans = -1;
        for (i = 0; i < N; i++)
        {
      
            // y is the length of the longest
            // UD sequence starting at i
            y = dp[i][1];
      
            if (i + y >= N)
                ans = Math.max(ans, dp[i][1] + 1);
      
            // If length is even then add an integer
            // and then a DU sequence starting at i + y
            else if (y % 2 == 0)
            {
                ans = Math.max(ans, dp[i][1] + 1 + dp[i + y][2]);
            }
      
            // If length is odd then add an integer
            // and then a UD sequence starting at i + y
            else if (y % 2 == 1)
            {
                ans = Math.max(ans, dp[i][1] + 1 + dp[i + y][1]);
            }
        }
        return ans;
    }
     
    let A = [ 1, 10, 3, 20, 25, 24 ];
    let n = A.length;
 
    document.write(maxLenSeq(A, n));
             
</script>

Producción:

Complejidad temporal: O(n)
Complejidad espacial: O(n)

Publicación traducida automáticamente

Artículo escrito por coder_maddy y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta