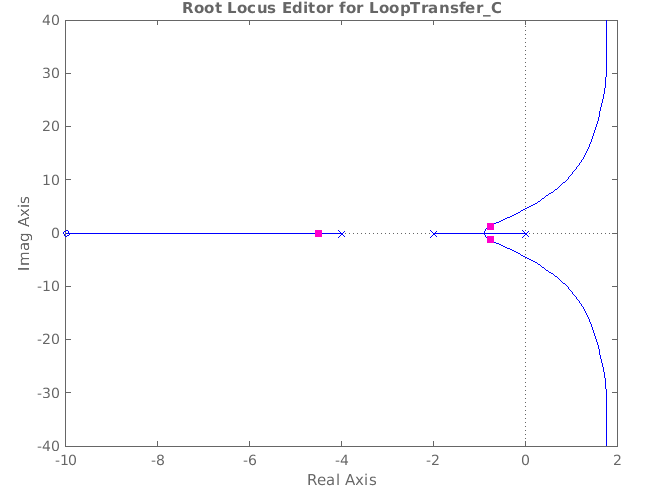
En los sistemas de control, el análisis del lugar geométrico de las raíces es una estrategia gráfica para observar cómo cambian los cimientos de un sistema con la variación de un límite específico del sistema, generalmente una adición dentro de un sistema de retroalimentación.
El propósito del lugar geométrico de las raíces en el sistema de control es el siguiente:
- Para encontrar la estabilidad
- Para comprobar si un punto está en el lugar geométrico de las raíces o no
- Para encontrar la ganancia del sistema, es decir, «k» o parámetro del sistema
Reglas de construcción de un lugar de raíces:
Regla 1: existirá un punto en el eje real, el lugar geométrico de las raíces se bifurca si la suma de polos y ceros a la derecha del punto debe ser impar.
Regla 2: Asíntotas: Son ramas del lugar geométrico de las raíces que comienzan en el eje real y se acercan al infinito.
Número de asíntotas “N = P – Z”
Aquí «P» es el número de polos y «Z» es el número de ceros
Regla 3: Ángulo de asíntotas
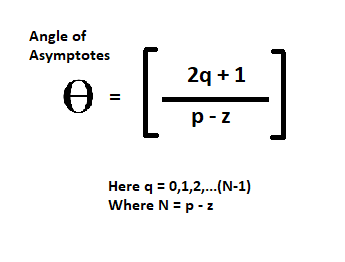
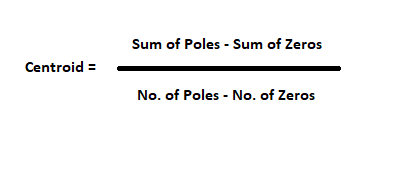
Regla 4: Centroide: el punto de encuentro de las asíntotas en el eje real se denomina centroide
Regla 5: Break Point (BP): Hay dos tipos
- Punto de ruptura (BAP)
- Punto de entrada (BIP)
Regla 6: Punto de intersección (IP) del lugar geométrico de las raíces con el eje imaginario.
Regla 7:
a) Ángulo de salida: Se calcula para polos complejos conjugados o polos imaginarios
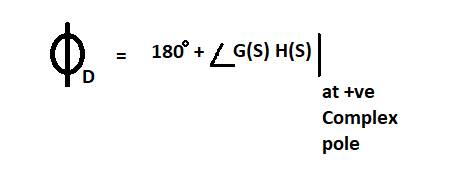
b) Ángulo de llegada: Se calcula para ceros complejos conjugados o ceros imaginarios
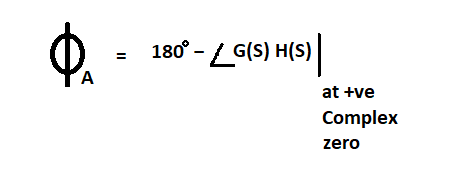
Código:
% Row of 1×2 NUM = [1 10]; % Row of 1×4 DEN = [1 6 8 0]; % Row of 1×2 poly1 = [1 2]; % Row of 1×2 poly2 = [1 4]; % convolves vectors poly1 and poly2, % multiplying the polynomials whose coefficients % are the elements of poly1 and poly2 poly = conv(poly1, poly2); % returns the roots of the polynomial % represented by DEN as a column vector roots(DEN); % Continuous time transfer function sys = tf(NUM, DEN); % GUI for per-forming Root Locus analysis rltool(sys);
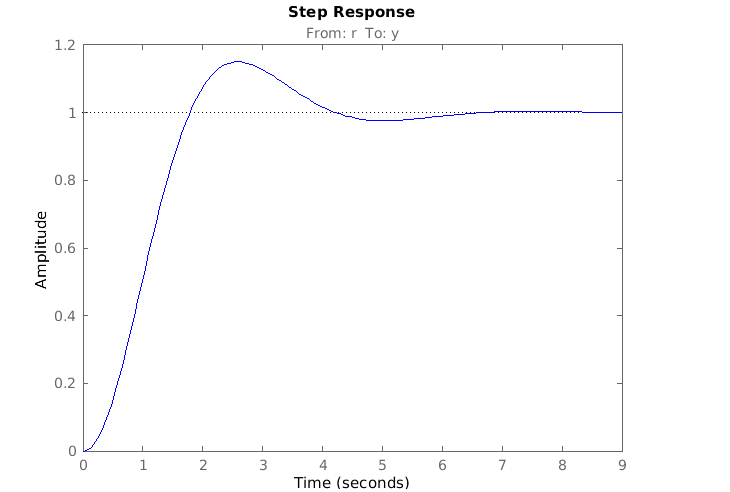
Producción :
Publicación traducida automáticamente
Artículo escrito por sourabhnaikssj y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA