Dado un gráfico no dirigido y un número m, determine si el gráfico puede colorearse con m colores como máximo, de modo que no haya dos vértices adyacentes del gráfico coloreados con el mismo color. Aquí la coloración de un gráfico significa la asignación de colores a todos los vértices.
Formato de entrada-salida:
Aporte:
- Un gráfico de array 2D[V][V] donde V es el número de vértices en el gráfico y el gráfico[V][V] es una representación de array de adyacencia del gráfico. Un valor de graph[i][j] es 1 si hay un borde directo de i a j, de lo contrario, graph[i][j] es 0.
- Un entero m es el número máximo de colores que se pueden utilizar.
Salida:
una array color[V] que debe tener números del 1 al m. color[i] debe representar el color asignado al i-ésimo vértice. El código también debería devolver falso si el gráfico no se puede colorear con m colores.
Ejemplo:
Input:
graph = {0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 1},
{1, 0, 1, 0}
Output:
Solution Exists:
Following are the assigned colors
1 2 3 2
Explanation: By coloring the vertices
with following colors, adjacent
vertices does not have same colors
Input:
graph = {1, 1, 1, 1},
{1, 1, 1, 1},
{1, 1, 1, 1},
{1, 1, 1, 1}
Output: Solution does not exist.
Explanation: No solution exits.
A continuación se muestra un ejemplo de un gráfico que se puede colorear con 3 colores diferentes.
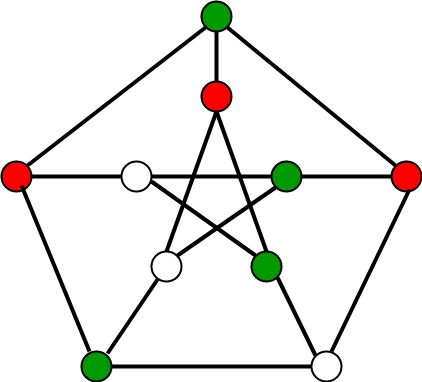
Le recomendamos encarecidamente que haga clic aquí y lo practique antes de pasar a la solución.
Método 1: Ingenuo.
Enfoque ingenuo: genera todas las configuraciones posibles de colores. Dado que cada Node se puede colorear con cualquiera de los m colores disponibles, el número total de configuraciones de color posibles es m^V.
Después de generar una configuración de color, comprueba si los vértices adyacentes tienen el mismo color o no. Si se cumplen las condiciones, imprima la combinación y rompa el ciclo.
Algoritmo:
- Cree una función recursiva que tome el índice actual, el número de vértices y la array de colores de salida.
- Si el índice actual es igual al número de vértices. Compruebe si la configuración del color de salida es segura, es decir, compruebe si los vértices adyacentes no tienen el mismo color. Si se cumplen las condiciones, imprima la configuración y rompa.
- Asigne un color a un vértice (1 a m).
- Para cada color asignado, llame recursivamente a la función con el siguiente índice y número de vértices
- Si alguna función recursiva devuelve verdadero, rompe el ciclo y devuelve verdadero.
A continuación se muestra la implementación de la idea anterior:
C++
#include<bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 4
void printSolution(int color[]);
// check if the colored
// graph is safe or not
bool isSafe(bool graph[V][V], int color[])
{
// check for every edge
for (int i = 0; i < V; i++)
for (int j = i + 1; j < V; j++)
if (graph[i][j] && color[j] == color[i])
return false;
return true;
}
/* This function solves the m Coloring
problem using recursion. It returns
false if the m colours cannot be assigned,
otherwise, return true and prints
assignments of colours to all vertices.
Please note that there may be more than
one solutions, this function prints one
of the feasible solutions.*/
bool graphColoring(bool graph[V][V], int m, int i,
int color[V])
{
// if current index reached end
if (i == V) {
// if coloring is safe
if (isSafe(graph, color)) {
// Print the solution
printSolution(color);
return true;
}
return false;
}
// Assign each color from 1 to m
for (int j = 1; j <= m; j++) {
color[i] = j;
// Recur of the rest vertices
if (graphColoring(graph, m, i + 1, color))
return true;
color[i] = 0;
}
return false;
}
/* A utility function to print solution */
void printSolution(int color[])
{
cout << "Solution Exists:" " Following are the assigned colors \n";
for (int i = 0; i < V; i++)
cout << " " << color[i];
cout << "\n";
}
// Driver code
int main()
{
/* Create following graph and
test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool graph[V][V] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
int m = 3; // Number of colors
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!graphColoring(graph, m, 0, color))
cout << "Solution does not exist";
return 0;
}
// This code is contributed by shivanisinghss2110
C
#include <stdbool.h>
#include <stdio.h>
// Number of vertices in the graph
#define V 4
void printSolution(int color[]);
// check if the colored
// graph is safe or not
bool isSafe(bool graph[V][V], int color[])
{
// check for every edge
for (int i = 0; i < V; i++)
for (int j = i + 1; j < V; j++)
if (graph[i][j] && color[j] == color[i])
return false;
return true;
}
/* This function solves the m Coloring
problem using recursion. It returns
false if the m colours cannot be assigned,
otherwise, return true and prints
assignments of colours to all vertices.
Please note that there may be more than
one solutions, this function prints one
of the feasible solutions.*/
bool graphColoring(bool graph[V][V], int m, int i,
int color[V])
{
// if current index reached end
if (i == V) {
// if coloring is safe
if (isSafe(graph, color)) {
// Print the solution
printSolution(color);
return true;
}
return false;
}
// Assign each color from 1 to m
for (int j = 1; j <= m; j++) {
color[i] = j;
// Recur of the rest vertices
if (graphColoring(graph, m, i + 1, color))
return true;
color[i] = 0;
}
return false;
}
/* A utility function to print solution */
void printSolution(int color[])
{
printf("Solution Exists:"
" Following are the assigned colors \n");
for (int i = 0; i < V; i++)
printf(" %d ", color[i]);
printf("\n");
}
// Driver program to test above function
int main()
{
/* Create following graph and
test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool graph[V][V] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
int m = 3; // Number of colors
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!graphColoring(graph, m, 0, color))
printf("Solution does not exist");
return 0;
}
Java
public class GFG
{
// Number of vertices in the graph
static int V = 4;
/* A utility function to print solution */
static void printSolution(int[] color)
{
System.out.println("Solution Exists:" +
" Following are the assigned colors ");
for (int i = 0; i < V; i++)
System.out.print(" " + color[i]);
System.out.println();
}
// check if the colored
// graph is safe or not
static boolean isSafe(boolean[][] graph, int[] color)
{
// check for every edge
for (int i = 0; i < V; i++)
for (int j = i + 1; j < V; j++)
if (graph[i][j] && color[j] == color[i])
return false;
return true;
}
/* This function solves the m Coloring
problem using recursion. It returns
false if the m colours cannot be assigned,
otherwise, return true and prints
assignments of colours to all vertices.
Please note that there may be more than
one solutions, this function prints one
of the feasible solutions.*/
static boolean graphColoring(boolean[][] graph, int m,
int i, int[] color)
{
// if current index reached end
if (i == V) {
// if coloring is safe
if (isSafe(graph, color))
{
// Print the solution
printSolution(color);
return true;
}
return false;
}
// Assign each color from 1 to m
for (int j = 1; j <= m; j++)
{
color[i] = j;
// Recur of the rest vertices
if (graphColoring(graph, m, i + 1, color))
return true;
color[i] = 0;
}
return false;
}
// Driver code
public static void main(String[] args)
{
/* Create following graph and
test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
boolean[][] graph = {
{ false, true, true, true },
{ true, false, true, false },
{ true, true, false, true },
{ true, false, true, false },
};
int m = 3; // Number of colors
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
int[] color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!graphColoring(graph, m, 0, color))
System.out.println("Solution does not exist");
}
}
// This code is contributed by divyeh072019.
Python3
# Number of vertices in the graph
# define 4 4
# check if the colored
# graph is safe or not
def isSafe(graph, color):
# check for every edge
for i in range(4):
for j in range(i + 1, 4):
if (graph[i][j] and color[j] == color[i]):
return False
return True
# /* This function solves the m Coloring
# problem using recursion. It returns
# false if the m colours cannot be assigned,
# otherwise, return true and prints
# assignments of colours to all vertices.
# Please note that there may be more than
# one solutions, this function prints one
# of the feasible solutions.*/
def graphColoring(graph, m, i, color):
# if current index reached end
if (i == 4):
# if coloring is safe
if (isSafe(graph, color)):
# Print the solution
printSolution(color)
return True
return False
# Assign each color from 1 to m
for j in range(1, m + 1):
color[i] = j
# Recur of the rest vertices
if (graphColoring(graph, m, i + 1, color)):
return True
color[i] = 0
return False
# /* A utility function to print solution */
def printSolution(color):
print("Solution Exists:" " Following are the assigned colors ")
for i in range(4):
print(color[i],end=" ")
# Driver code
if __name__ == '__main__':
# /* Create following graph and
# test whether it is 3 colorable
# (3)---(2)
# | / |
# | / |
# | / |
# (0)---(1)
# */
graph = [
[ 0, 1, 1, 1 ],
[ 1, 0, 1, 0 ],
[ 1, 1, 0, 1 ],
[ 1, 0, 1, 0 ],
]
m = 3 # Number of colors
# Initialize all color values as 0.
# This initialization is needed
# correct functioning of isSafe()
color = [0 for i in range(4)]
if (not graphColoring(graph, m, 0, color)):
print ("Solution does not exist")
# This code is contributed by mohit kumar 29
C#
using System;
class GFG {
// Number of vertices in the graph
static int V = 4;
/* A utility function to print solution */
static void printSolution(int[] color)
{
Console.WriteLine("Solution Exists:" +
" Following are the assigned colors ");
for (int i = 0; i < V; i++)
Console.Write(" " + color[i]);
Console.WriteLine();
}
// check if the colored
// graph is safe or not
static bool isSafe(bool[,] graph, int[] color)
{
// check for every edge
for (int i = 0; i < V; i++)
for (int j = i + 1; j < V; j++)
if (graph[i, j] && color[j] == color[i])
return false;
return true;
}
/* This function solves the m Coloring
problem using recursion. It returns
false if the m colours cannot be assigned,
otherwise, return true and prints
assignments of colours to all vertices.
Please note that there may be more than
one solutions, this function prints one
of the feasible solutions.*/
static bool graphColoring(bool[,] graph, int m,
int i, int[] color)
{
// if current index reached end
if (i == V) {
// if coloring is safe
if (isSafe(graph, color)) {
// Print the solution
printSolution(color);
return true;
}
return false;
}
// Assign each color from 1 to m
for (int j = 1; j <= m; j++) {
color[i] = j;
// Recur of the rest vertices
if (graphColoring(graph, m, i + 1, color))
return true;
color[i] = 0;
}
return false;
}
// Driver code
static void Main() {
/* Create following graph and
test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool[,] graph = {
{ false, true, true, true },
{ true, false, true, false },
{ true, true, false, true },
{ true, false, true, false },
};
int m = 3; // Number of colors
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
int[] color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
if (!graphColoring(graph, m, 0, color))
Console.WriteLine("Solution does not exist");
}
}
// this code is contributed by divyeshrabadiya07.
Javascript
<script>
// Number of vertices in the graph
let V = 4;
/* A utility function to print solution */
function printSolution(color)
{
document.write("Solution Exists:" +
" Following are the assigned colors <br>");
for (let i = 0; i < V; i++)
document.write(" " + color[i]);
document.write(" ");
}
// check if the colored
// graph is safe or not
function isSafe(graph,color)
{
// check for every edge
for (let i = 0; i < V; i++)
for (let j = i + 1; j < V; j++)
if (graph[i][j] && color[j] == color[i])
return false;
return true;
}
/* This function solves the m Coloring
problem using recursion. It returns
false if the m colours cannot be assigned,
otherwise, return true and prints
assignments of colours to all vertices.
Please note that there may be more than
one solutions, this function prints one
of the feasible solutions.*/
function graphColoring(graph,m,i,color)
{
// if current index reached end
if (i == V) {
// if coloring is safe
if (isSafe(graph, color))
{
// Print the solution
printSolution(color);
return true;
}
return false;
}
// Assign each color from 1 to m
for (let j = 1; j <= m; j++)
{
color[i] = j;
// Recur of the rest vertices
if (graphColoring(graph, m, i + 1, color))
return true;
color[i] = 0;
}
return false;
}
// Driver code
/* Create following graph and
test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
let graph=[[ false, true, true, true],
[ true, false, true, false ],
[ true, true, false, true ],
[true, false, true, false]];
let m = 3; // Number of colors
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
let color = new Array(V);
for (let i = 0; i < V; i++)
color[i] = 0;
if (!graphColoring(graph, m, 0, color))
document.write("Solution does not exist");
// This code is contributed by unknown2108
</script>
Solution Exists: Following are the assigned colors 1 2 3 2
Análisis de Complejidad:
- Complejidad temporal: O(m^V).
Hay una combinación total de colores O(m^V). Entonces la complejidad del tiempo es O(m^V). - Complejidad espacial: O(V).
La pila recursiva de la función graphColoring(…) requerirá espacio O(V).
Método 2 : Retroceder .
Enfoque: La idea es asignar colores uno por uno a diferentes vértices, comenzando desde el vértice 0. Antes de asignar un color, verifique la seguridad considerando los colores ya asignados a los vértices adyacentes, es decir, verifique si los vértices adyacentes tienen el mismo color o no. . Si hay alguna asignación de color que no viole las condiciones, marque la asignación de color como parte de la solución. Si no es posible asignar un color, retroceda y devuelva falso.
Algoritmo:
- Cree una función recursiva que tome el gráfico, el índice actual, el número de vértices y la array de colores de salida.
- Si el índice actual es igual al número de vértices. Imprima la configuración de color en la array de salida.
- Asigne un color a un vértice (1 a m).
- Para cada color asignado, verifique si la configuración es segura (es decir, verifique si los vértices adyacentes no tienen el mismo color) llame recursivamente a la función con el siguiente índice y número de vértices
- Si alguna función recursiva devuelve verdadero, rompa el ciclo y devuelva verdadero.
- Si ninguna función recursiva devuelve verdadero, devuelve falso.
A continuación se muestra la implementación de la idea anterior:
C++
// C++ program for solution of M
// Coloring problem using backtracking
#include <iostream>
using namespace std;
// Number of vertices in the graph
#define V 4
void printSolution(int color[]);
/* A utility function to check if
the current color assignment
is safe for vertex v i.e. checks
whether the edge exists or not
(i.e, graph[v][i]==1). If exist
then checks whether the color to
be filled in the new vertex(c is
sent in the parameter) is already
used by its adjacent
vertices(i-->adj vertices) or
not (i.e, color[i]==c) */
bool isSafe(int v, bool graph[V][V],
int color[], int c)
{
for(int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
/* A recursive utility function
to solve m coloring problem */
bool graphColoringUtil(bool graph[V][V], int m,
int color[], int v)
{
/* base case: If all vertices are
assigned a color then return true */
if (v == V)
return true;
/* Consider this vertex v and
try different colors */
for(int c = 1; c <= m; c++)
{
/* Check if assignment of color
c to v is fine*/
if (isSafe(v, graph, color, c))
{
color[v] = c;
/* recur to assign colors to
rest of the vertices */
if (graphColoringUtil(
graph, m, color, v + 1) == true)
return true;
/* If assigning color c doesn't
lead to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to
this vertex then return false */
return false;
}
/* This function solves the m Coloring
problem using Backtracking. It mainly
uses graphColoringUtil() to solve the
problem. It returns false if the m
colors cannot be assigned, otherwise
return true and prints assignments of
colors to all vertices. Please note
that there may be more than one solutions,
this function prints one of the
feasible solutions.*/
bool graphColoring(bool graph[V][V], int m)
{
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
int color[V];
for(int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (graphColoringUtil(graph, m, color, 0) == false)
{
cout << "Solution does not exist";
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
cout << "Solution Exists:"
<< " Following are the assigned colors"
<< "\n";
for(int i = 0; i < V; i++)
cout << " " << color[i] << " ";
cout << "\n";
}
// Driver code
int main()
{
/* Create following graph and test
whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool graph[V][V] = { { 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 }, };
// Number of colors
int m = 3;
graphColoring(graph, m);
return 0;
}
// This code is contributed by Shivani
C
#include <stdbool.h>
#include <stdio.h>
// Number of vertices in the graph
#define V 4
void printSolution(int color[]);
/* A utility function to check if
the current color assignment
is safe for vertex v i.e. checks
whether the edge exists or not
(i.e, graph[v][i]==1). If exist
then checks whether the color to
be filled in the new vertex(c is
sent in the parameter) is already
used by its adjacent
vertices(i-->adj vertices) or
not (i.e, color[i]==c) */
bool isSafe(
int v, bool graph[V][V],
int color[], int c)
{
for (int i = 0; i < V; i++)
if (
graph[v][i] && c == color[i])
return false;
return true;
}
/* A recursive utility function
to solve m coloring problem */
bool graphColoringUtil(
bool graph[V][V], int m,
int color[], int v)
{
/* base case: If all vertices are
assigned a color then return true */
if (v == V)
return true;
/* Consider this vertex v and
try different colors */
for (int c = 1; c <= m; c++) {
/* Check if assignment of color
c to v is fine*/
if (isSafe(
v, graph, color, c)) {
color[v] = c;
/* recur to assign colors to
rest of the vertices */
if (
graphColoringUtil(
graph, m, color, v + 1)
== true)
return true;
/* If assigning color c doesn't
lead to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to
this vertex then return false */
return false;
}
/* This function solves the m Coloring
problem using Backtracking. It mainly
uses graphColoringUtil() to solve the
problem. It returns false if the m
colors cannot be assigned, otherwise
return true and prints assignments of
colors to all vertices. Please note
that there may be more than one solutions,
this function prints one of the
feasible solutions.*/
bool graphColoring(
bool graph[V][V], int m)
{
// Initialize all color values as 0.
// This initialization is needed
// correct functioning of isSafe()
int color[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (
graphColoringUtil(
graph, m, color, 0)
== false) {
printf("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
printf(
"Solution Exists:"
" Following are the assigned colors \n");
for (int i = 0; i < V; i++)
printf(" %d ", color[i]);
printf("\n");
}
// driver program to test above function
int main()
{
/* Create following graph and test
whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool graph[V][V] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
int m = 3; // Number of colors
graphColoring(graph, m);
return 0;
}
Java
/* Java program for solution of
M Coloring problem using backtracking */
public class mColoringProblem
{
final int V = 4;
int color[];
/* A utility function to check
if the current color assignment
is safe for vertex v */
boolean isSafe(
int v, int graph[][], int color[],
int c)
{
for (int i = 0; i < V; i++)
if (
graph[v][i] == 1 && c == color[i])
return false;
return true;
}
/* A recursive utility function
to solve m coloring problem */
boolean graphColoringUtil(
int graph[][], int m,
int color[], int v)
{
/* base case: If all vertices are
assigned a color then return true */
if (v == V)
return true;
/* Consider this vertex v and try
different colors */
for (int c = 1; c <= m; c++)
{
/* Check if assignment of color c to v
is fine*/
if (isSafe(v, graph, color, c))
{
color[v] = c;
/* recur to assign colors to rest
of the vertices */
if (
graphColoringUtil(
graph, m,
color, v + 1))
return true;
/* If assigning color c doesn't lead
to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to
this vertex then return false */
return false;
}
/* This function solves the m Coloring problem using
Backtracking. It mainly uses graphColoringUtil()
to solve the problem. It returns false if the m
colors cannot be assigned, otherwise return true
and prints assignments of colors to all vertices.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
boolean graphColoring(int graph[][], int m)
{
// Initialize all color values as 0. This
// initialization is needed correct
// functioning of isSafe()
color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (
!graphColoringUtil(
graph, m, color, 0))
{
System.out.println(
"Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
System.out.println(
"Solution Exists: Following"
+ " are the assigned colors");
for (int i = 0; i < V; i++)
System.out.print(" " + color[i] + " ");
System.out.println();
}
// driver program to test above function
public static void main(String args[])
{
mColoringProblem Coloring
= new mColoringProblem();
/* Create following graph and
test whether it is
3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
int graph[][] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 },
};
int m = 3; // Number of colors
Coloring.graphColoring(graph, m);
}
}
// This code is contributed by Abhishek Shankhadhar
Python3
# Python program for solution of M Coloring
# problem using backtracking
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]\
for row in range(vertices)]
# A utility function to check
# if the current color assignment
# is safe for vertex v
def isSafe(self, v, colour, c):
for i in range(self.V):
if self.graph[v][i] == 1 and colour[i] == c:
return False
return True
# A recursive utility function to solve m
# coloring problem
def graphColourUtil(self, m, colour, v):
if v == self.V:
return True
for c in range(1, m + 1):
if self.isSafe(v, colour, c) == True:
colour[v] = c
if self.graphColourUtil(m, colour, v + 1) == True:
return True
colour[v] = 0
def graphColouring(self, m):
colour = [0] * self.V
if self.graphColourUtil(m, colour, 0) == None:
return False
# Print the solution
print ("Solution exist and Following are the assigned colours:")
for c in colour:
print (c,end=' ')
return True
# Driver Code
g = Graph(4)
g.graph = [[0, 1, 1, 1], [1, 0, 1, 0], [1, 1, 0, 1], [1, 0, 1, 0]]
m = 3
g.graphColouring(m)
# This code is contributed by Divyanshu Mehta
C#
/* C# program for solution of M Coloring problem
using backtracking */
using System;
class GFG {
readonly int V = 4;
int[] color;
/* A utility function to check if the current
color assignment is safe for vertex v */
bool isSafe(int v, int[, ] graph,
int[] color, int c)
{
for (int i = 0; i < V; i++)
if (graph[v, i] == 1 && c == color[i])
return false;
return true;
}
/* A recursive utility function to solve m
coloring problem */
bool graphColoringUtil(int[, ] graph, int m,
int[] color, int v)
{
/* base case: If all vertices are assigned
a color then return true */
if (v == V)
return true;
/* Consider this vertex v and try different
colors */
for (int c = 1; c <= m; c++) {
/* Check if assignment of color c to v
is fine*/
if (isSafe(v, graph, color, c)) {
color[v] = c;
/* recur to assign colors to rest
of the vertices */
if (graphColoringUtil(graph, m,
color, v + 1))
return true;
/* If assigning color c doesn't lead
to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to this vertex
then return false */
return false;
}
/* This function solves the m Coloring problem using
Backtracking. It mainly uses graphColoringUtil()
to solve the problem. It returns false if the m
colors cannot be assigned, otherwise return true
and prints assignments of colors to all vertices.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool graphColoring(int[, ] graph, int m)
{
// Initialize all color values as 0. This
// initialization is needed correct functioning
// of isSafe()
color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (!graphColoringUtil(graph, m, color, 0)) {
Console.WriteLine("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int[] color)
{
Console.WriteLine("Solution Exists: Following"
+ " are the assigned colors");
for (int i = 0; i < V; i++)
Console.Write(" " + color[i] + " ");
Console.WriteLine();
}
// Driver Code
public static void Main(String[] args)
{
GFG Coloring = new GFG();
/* Create following graph and test whether it is
3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
int[, ] graph = { { 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 } };
int m = 3; // Number of colors
Coloring.graphColoring(graph, m);
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
/* JavaScript program for solution of
M Coloring problem using backtracking */
let V = 4;
let color;
/* A utility function to check
if the current color assignment
is safe for vertex v */
function isSafe(v,graph,color,c)
{
for (let i = 0; i < V; i++)
if (
graph[v][i] == 1 && c == color[i])
return false;
return true;
}
/* A recursive utility function
to solve m coloring problem */
function graphColoringUtil(graph,m,color,v)
{
/* base case: If all vertices are
assigned a color then return true */
if (v == V)
return true;
/* Consider this vertex v and try
different colors */
for (let c = 1; c <= m; c++)
{
/* Check if assignment of color c to v
is fine*/
if (isSafe(v, graph, color, c))
{
color[v] = c;
/* recur to assign colors to rest
of the vertices */
if (
graphColoringUtil(
graph, m,
color, v + 1))
return true;
/* If assigning color c doesn't lead
to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to
this vertex then return false */
return false;
}
/* This function solves the m Coloring problem using
Backtracking. It mainly uses graphColoringUtil()
to solve the problem. It returns false if the m
colors cannot be assigned, otherwise return true
and prints assignments of colors to all vertices.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
function graphColoring(graph,m)
{
// Initialize all color values as 0. This
// initialization is needed correct
// functioning of isSafe()
color = new Array(V);
for (let i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (
!graphColoringUtil(
graph, m, color, 0))
{
document.write(
"Solution does not exist<br>");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
function printSolution(color)
{
document.write(
"Solution Exists: Following"
+ " are the assigned colors<br>");
for (let i = 0; i < V; i++)
document.write(" " + color[i] + " ");
document.write("<br>");
}
// driver program to test above function
/* Create following graph and
test whether it is
3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
let graph = [
[ 0, 1, 1, 1 ],
[ 1, 0, 1, 0 ],
[ 1, 1, 0, 1 ],
[ 1, 0, 1, 0 ],
];
let m = 3; // Number of colors
graphColoring(graph, m);
// This code is contributed by ab2127
</script>
Solution Exists: Following are the assigned colors 1 2 3 2
Análisis de Complejidad:
- Complejidad temporal: O(m^V).
Hay una combinación total de colores O(m^V). Entonces la complejidad del tiempo es O(m^V). La complejidad del tiempo de límite superior sigue siendo la misma, pero el tiempo medio necesario será menor. - Complejidad espacial: O(V).
La pila recursiva de la función graphColoring(…) requerirá espacio O(V).
Método 3: Usar BFS
El enfoque aquí es colorear cada Node del 1 al n inicialmente con el color 1. Y comenzar a viajar BFS desde un Node inicial no visitado para cubrir todos los componentes conectados de una sola vez. Al llegar a cada Node durante el recorrido de BFS, haga lo siguiente:
- Verifique todos los bordes del Node dado.
- Para cada vértice conectado a nuestro Node a través de un borde:
- compruebe si el color de los Nodes es el mismo. Si es el mismo, aumente el color del otro Node (no el actual) en uno.
- comprobar si visitó o no visitó. Si no lo visitó, márquelo como visitado y colóquelo en una cola.
- Compruebe el estado de maxColors hasta ahora. Si excede M, devuelve falso
Después de visitar todos los Nodes, devuelva verdadero (ya que no se pudo encontrar ninguna condición violatoria durante el viaje).
C++
// CPP program for the above approach
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
class node
{
// A node class which stores the color and the edges
// connected to the node
public:
int color = 1;
set<int> edges;
};
int canPaint(vector<node>& nodes, int n, int m)
{
// Create a visited array of n
// nodes, initialized to zero
vector<int> visited(n + 1, 0);
// maxColors used till now are 1 as
// all nodes are painted color 1
int maxColors = 1;
// Do a full BFS traversal from
// all unvisited starting points
for (int sv = 1; sv <= n; sv++)
{
if (visited[sv])
continue;
// If the starting point is unvisited,
// mark it visited and push it in queue
visited[sv] = 1;
queue<int> q;
q.push(sv);
// BFS Travel starts here
while (!q.empty())
{
int top = q.front();
q.pop();
// Checking all adjacent nodes
// to "top" edge in our queue
for (auto it = nodes[top].edges.begin();
it != nodes[top].edges.end(); it++)
{
// IMPORTANT: If the color of the
// adjacent node is same, increase it by 1
if (nodes[top].color == nodes[*it].color)
nodes[*it].color += 1;
// If number of colors used shoots m, return
// 0
maxColors
= max(maxColors, max(nodes[top].color,
nodes[*it].color));
if (maxColors > m)
return 0;
// If the adjacent node is not visited,
// mark it visited and push it in queue
if (!visited[*it]) {
visited[*it] = 1;
q.push(*it);
}
}
}
}
return 1;
}
// Driver code
int main()
{
int n = 4;
bool graph[n][n] = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 }};
int m = 3; // Number of colors
// Create a vector of n+1
// nodes of type "node"
// The zeroth position is just
// dummy (1 to n to be used)
vector<node> nodes(n + 1);
// Add edges to each node as per given input
for (int i = 0; i < n; i++)
{
for(int j =0;j<n;j++)
{
if(graph[i][j])
{
// Connect the undirected graph
nodes[i].edges.insert(i);
nodes[j].edges.insert(j);
}
}
}
// Display final answer
cout << canPaint(nodes, n, m);
cout << "\n";
return 0;
}
Java
// Java program for the above approach
import java.io.*;
import java.util.*;
class Node
{
// A node class which stores the color and the edges
// connected to the node
int color = 1;
Set<Integer> edges = new HashSet<Integer>();
}
class GFG
{
static int canPaint(ArrayList<Node> nodes, int n, int m)
{
// Create a visited array of n
// nodes, initialized to zero
ArrayList<Integer> visited = new ArrayList<Integer>();
for(int i = 0; i < n + 1; i++)
{
visited.add(0);
}
// maxColors used till now are 1 as
// all nodes are painted color 1
int maxColors = 1;
// Do a full BFS traversal from
// all unvisited starting points
for (int sv = 1; sv <= n; sv++)
{
if (visited.get(sv) > 0)
{
continue;
}
// If the starting point is unvisited,
// mark it visited and push it in queue
visited.set(sv, 1);
Queue<Integer> q = new LinkedList<>();
q.add(sv);
// BFS Travel starts here
while(q.size() != 0)
{
int top = q.peek();
q.remove();
// Checking all adjacent nodes
// to "top" edge in our queue
for(int it: nodes.get(top).edges)
{
// IMPORTANT: If the color of the
// adjacent node is same, increase it by 1
if(nodes.get(top).color == nodes.get(it).color)
{
nodes.get(it).color += 1;
}
// If number of colors used shoots m, return
// 0
maxColors = Math.max(maxColors,
Math.max(nodes.get(top).color,
nodes.get(it).color));
if (maxColors > m)
return 0;
// If the adjacent node is not visited,
// mark it visited and push it in queue
if (visited.get(it) == 0)
{
visited.set(it, 1);
q.add(it);
}
}
}
}
return 1;
}
// Driver code
public static void main (String[] args)
{
int n = 4;
int [][] graph = {{ 0, 1, 1, 1 },{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },{ 1, 0, 1, 0 }};
int m = 3; // Number of colors
// Create a vector of n+1
// nodes of type "node"
// The zeroth position is just
// dummy (1 to n to be used)
ArrayList<Node> nodes = new ArrayList<Node>();
for(int i = 0; i < n+ 1; i++)
{
nodes.add(new Node());
}
// Add edges to each node as per given input
for (int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if(graph[i][j] > 0)
{
// Connect the undirected graph
nodes.get(i).edges.add(i);
nodes.get(j).edges.add(j);
}
}
}
// Display final answer
System.out.println(canPaint(nodes, n, m));
}
}
// This code is contributed by avanitrachhadiya2155
Python3
# Python3 program for the above approach from queue import Queue class node: color = 1 edges = set() def canPaint(nodes, n, m): # Create a visited array of n # nodes, initialized to zero visited = [0 for _ in range(n+1)] # maxColors used till now are 1 as # all nodes are painted color 1 maxColors = 1 # Do a full BFS traversal from # all unvisited starting points for _ in range(1, n + 1): if visited[_]: continue # If the starting point is unvisited, # mark it visited and push it in queue visited[_] = 1 q = Queue() q.put(_) # BFS Travel starts here while not q.empty(): top = q.get() # Checking all adjacent nodes # to "top" edge in our queue for _ in nodes[top].edges: # IMPORTANT: If the color of the # adjacent node is same, increase it by 1 if nodes[top].color == nodes[_].color: nodes[_].color += 1 # If number of colors used shoots m, # return 0 maxColors = max(maxColors, max( nodes[top].color, nodes[_].color)) if maxColors > m: print(maxColors) return 0 # If the adjacent node is not visited, # mark it visited and push it in queue if not visited[_]: visited[_] = 1 q.put(_) return 1 # Driver code if __name__ == "__main__": n = 4 graph = [ [ 0, 1, 1, 1 ], [ 1, 0, 1, 0 ], [ 1, 1, 0, 1 ], [ 1, 0, 1, 0 ] ] # Number of colors m = 3 # Create a vector of n+1 # nodes of type "node" # The zeroth position is just # dummy (1 to n to be used) nodes = [] for _ in range(n+1): nodes.append(node()) # Add edges to each node as # per given input for _ in range(n): for __ in range(n): if graph[_][__]: # Connect the undirected graph nodes[_].edges.add(_) nodes[__].edges.add(__) # Display final answer print(canPaint(nodes, n, m)) # This code is contributed by harshitkap00r
C#
// C# program for the above approach
using System;
using System.Collections;
using System.Collections.Generic;
class GFG
{
class node
{
// A node class which stores the color and the edges
// connected to the node
public int color = 1;
public HashSet<int> edges = new HashSet<int>();
};
static int canPaint(List<node> nodes, int n, int m)
{
// Create a visited array of n
// nodes, initialized to zero
List<int> visited = new List<int>();
for(int i = 0; i < n + 1; i++)
{
visited.Add(0);
}
// maxColors used till now are 1 as
// all nodes are painted color 1
int maxColors = 1;
// Do a full BFS traversal from
// all unvisited starting points
for (int sv = 1; sv <= n; sv++)
{
if (visited[sv] > 0)
continue;
// If the starting point is unvisited,
// mark it visited and push it in queue
visited[sv] = 1;
Queue q = new Queue();
q.Enqueue(sv);
// BFS Travel starts here
while (q.Count != 0)
{
int top = (int)q.Peek();
q.Dequeue();
// Checking all adjacent nodes
// to "top" edge in our queue
foreach(int it in nodes[top].edges)
{
// IMPORTANT: If the color of the
// adjacent node is same, increase it by 1
if (nodes[top].color == nodes[it].color)
nodes[it].color += 1;
// If number of colors used shoots m, return
// 0
maxColors
= Math.Max(maxColors, Math.Max(nodes[top].color,
nodes[it].color));
if (maxColors > m)
return 0;
// If the adjacent node is not visited,
// mark it visited and push it in queue
if (visited[it] == 0)
{
visited[it] = 1;
q.Enqueue(it);
}
}
}
}
return 1;
}
// Driver code
public static void Main()
{
int n = 4;
int [,]graph = {
{ 0, 1, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 1 },
{ 1, 0, 1, 0 }};
int m = 3; // Number of colors
// Create a vector of n+1
// nodes of type "node"
// The zeroth position is just
// dummy (1 to n to be used)
List<node> nodes = new List<node>();
for(int i = 0; i < n+ 1; i++)
{
nodes.Add(new node());
}
// Add edges to each node as per given input
for (int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
if(graph[i, j] > 0)
{
// Connect the undirected graph
nodes[i].edges.Add(i);
nodes[j].edges.Add(j);
}
}
}
// Display final answer
Console.WriteLine(canPaint(nodes, n, m));
}
}
// This code is contributed by rutvik_56.
Javascript
<script>
// Javascript program for the above approach
class node
{
// A node class which stores the color
// and the edges connected to the node
constructor()
{
this.color = 1;
this.edges = new Set();
}
};
function canPaint(nodes, n, m)
{
// Create a visited array of n
// nodes, initialized to zero
var visited = [];
for(var i = 0; i < n + 1; i++)
{
visited.push(0);
}
// maxColors used till now are 1 as
// all nodes are painted color 1
var maxColors = 1;
// Do a full BFS traversal from
// all unvisited starting points
for(var sv = 1; sv <= n; sv++)
{
if (visited[sv] > 0)
continue;
// If the starting point is unvisited,
// mark it visited and push it in queue
visited[sv] = 1;
var q = [];
q.push(sv);
// BFS Travel starts here
while (q.length != 0)
{
var top = q[0];
q.shift();
// Checking all adjacent nodes
// to "top" edge in our queue
for(var it of nodes[top].edges)
{
// IMPORTANT: If the color of the
// adjacent node is same, increase it by 1
if (nodes[top].color == nodes[it].color)
nodes[it].color += 1;
// If number of colors used shoots m, return
// 0
maxColors = Math.max(maxColors, Math.max(
nodes[top].color,
nodes[it].color));
if (maxColors > m)
return 0;
// If the adjacent node is not visited,
// mark it visited and push it in queue
if (visited[it] == 0)
{
visited[it] = 1;
q.push(it);
}
}
}
}
return 1;
}
// Driver code
var n = 4;
var graph = [ [ 0, 1, 1, 1 ],
[ 1, 0, 1, 0 ],
[ 1, 1, 0, 1 ],
[ 1, 0, 1, 0 ] ];
// Number of colors
var m = 3;
// Create a vector of n+1
// nodes of type "node"
// The zeroth position is just
// dummy (1 to n to be used)
var nodes = [];
for(var i = 0; i < n+ 1; i++)
{
nodes.push(new node());
}
// Push edges to each node as per given input
for (var i = 0; i < n; i++)
{
for(var j = 0; j < n; j++)
{
if(graph[i, j] > 0)
{
// Connect the undirected graph
nodes[i].edges.push(i);
nodes[j].edges.push(j);
}
}
}
// Display final answer
document.write(canPaint(nodes, n, m));
// This code is contributed by rrrtnx
</script>
1
Análisis de Complejidad:
- Complejidad Temporal: O(V + E).
- Complejidad espacial: O(V). Para almacenar la lista de visitas.
Referencias:
http://en.wikipedia.org/wiki/Graph_coloring
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA