Mapa de variables entrantes (VEM) en lógica digital – Part 1

Requisito previo: mapa de Karnaugh (K-map)
K-map es la mejor técnica manual para resolver ecuaciones booleanas, pero se vuelve difícil de manejar cuando el número de variables excede 5 o 6. Por lo tanto, se utiliza una técnica llamada Variable Entrant Map (VEM) para aumentar el tamaño efectivo de k-map. Permite que un mapa más pequeño maneje una gran cantidad de variables. Esto se hace escribiendo la salida en términos de entrada.

Ejemplo: una función de 3 variables se puede definir como una función de 2 variables si la salida se escribe en términos de la tercera variable.

Considere una función F(A,B,C) = (0,1,2,5)

Si definimos F en términos de ‘C’, entonces esta función se puede escribir como:

Y el VEM para esto es:

Ventajas de usar VEM –

• Se puede usar un VEM para trazar más de ‘n’ variables usando un mapa K de ‘n’ variable.
• Se usa comúnmente para resolver problemas que involucran multiplexores.

Procedimiento de minimización para VEM: ahora, veamos cómo encontrar la expresión SOP si se proporciona un VEM.

1. Escriba todas las variables (las formas originales y complementadas se tratan como dos variables diferentes) en el mapa como 0, deje 0, términos mínimos y no importa como están y obtenga la expresión SOP.
2. (a) Seleccione una variable y haga todas las apariciones de esa variable como 1, escriba minitérminos (1) como no importa, deje 0 y no importa como están. Ahora, obtenga la expresión SOP.
   (b) Multiplique la expresión SOP obtenida con la variable en cuestión.
3. Repita el paso 2 para todas las variables en el mapa k.
4. SOP de VEM se obtiene ORing todas las expresiones SOP obtenidas.

Apliquemos el procedimiento anterior en un VEM de muestra (X se usa para representar que no me importa):

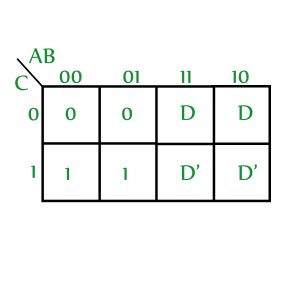
Paso 1: Escriba todas las variables como 0 (D y D’ se consideran como dos variables diferentes), deje los minitérminos, 0 y no importa como están y obtenga la expresión SOP.

 SOP obtained: A'C

Paso 2:
(a) Reemplace todas las apariciones de D con 1, todas las apariciones de D’ con 0 y todas las 1 con no importa. Deje 0 y no le importa como está.

(b) Multiplique el SOP obtenido con la variable en cuestión.

SOP obtained: AC'D

Paso 3: Repita el paso 2 para D’

(a) Reemplace todas las apariciones de D’ con 1, todas las apariciones de D con 0 y todas las 1 con no importa. Deje 0 y no le importa como está.

(b) Multiplique el SOP obtenido con la variable en cuestión.

SOP obtained: CD' 

Paso 4: el SOP de VEM se obtiene mediante la operación OR de todas las expresiones SOP obtenidas. Por lo tanto, la expresión SOP para el VEM dado es:

A'C + AC'D + CD'