Matemáticas | Anillos, dominios integrales y campos

Prerrequisito – Matemáticas | Estructura algebraica

Anillo: sean suma (+) y multiplicación (.) dos operaciones binarias definidas en un conjunto no vacío R. Entonces se dice que R forma un anillo con suma (+) y multiplicación (.) si se cumplen las siguientes condiciones:

(R, +) es un grupo abeliano (es decir, un grupo conmutativo)
(R, .) es un semigrupo
Para tres elementos cualesquiera a, b, c $\epsilon$ R se cumple la ley distributiva izquierda a.(b+c) =ab + ac y la propiedad distributiva derecha (b + c).a =ba + ca.

Por lo tanto, un conjunto R no vacío es un anillo de las operaciones binarias + y . si se cumplen las siguientes condiciones.

Para todo a, b $\epsilon$ R, a+b $\epsilon$ R,
Para todo a, b, c $\epsilon$ R a+(b+c)=(a+b)+c,
Existe un elemento en R, denotado por 0 tal que a+0=a para todo a $\epsilon$ R
Para todo a $\epsilon$ R existe un y $\epsilon$ R tal que a+y=0. y generalmente se denota por -a
a+b=b+a para todo a, b $\epsilon$ R.
ab $\epsilon$ R para todo ab $\epsilon$ R.
a.(bc)=(ab).c para todo a, b $\epsilon$ R
Para tres elementos cualesquiera a, b, c $\epsilon$ R a.(b+c) =ab + ac y (b + c).a =ba + ca Y el anillo se denota por (R, +, .).

Algunos ejemplos –

( $\mathbb{Z}$ , + ) es un grupo conmutativo .( $\mathbb{Z}$ , .) es un semigrupo. La ley distributiva también se cumple. Entonces, (( $\mathbb{Z}$ , +, .) es un anillo.
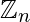Anillo de enteros módulo n: Para un $\epsilon$ [Tex]\mathbb{N} [/Tex] $\mathbb Z_n$ sean las clases de residuos de enteros módulo nie $\mathbb Z_n$ ={ $\bar{0}, \bar{1}, \bar{2}, ......., \overline{n-1}$ ).
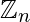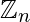( $\mathbb Z_n$ , +) es un grupo conmutativo ere + es suma (mod n).
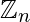( $\mathbb Z_n$ , .) es un semigrupo aquí . denota multiplicación (mod n).
También se cumplen las leyes distributivas. Entonces ((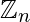 $\mathbb Z_n$ , +, .) es un anillo.
El conjunto S = {0, 1, 2, 3, 4} es un anillo con respecto a la operación suma módulo 5 y multiplicación módulo 5.

(S,+5) es un Grupo Abeliano. De la primera tabla de composición anterior podemos concluir que (S,+5) satisface –

Cierre : a ∈ S ,b ∈ S => a + ₅ b ∈ S ; ∀ a,b ∈ S
Asociatividad : (a+ ₅ b)+5c = a+ ₅ (b+ ₅ c) ; ∀ a,b,c ∈ S.
Existencia de identidad 0 : (a+ ₅ b)+ ₅ c = a+ ₅ (b+ ₅ c) ; ∀ a,b,c ∈ S.
Existencia de inverso: Inverso de 0, 1, 2, 3, 4 son 0, 4, 3, 2, 1 respectivamente &
Conmutativo: (a+ ₅ b) = (b+ ₅ a) ; ∀ a,b ∈ S

2. (S,* ₅ ) es un Semi Grupo. De la segunda tabla de composición anterior podemos concluir que (S,* ₅ ) satisface:

Cierre : a ∈ S ,b ∈ S => a * ₅ b ∈ S ; ∀ a,b ∈ S
Asociatividad : (a* ₅ b)* ₅ c = a* ₅ (b* ₅ c) ; ∀ a,b,c ∈ S

3. La multiplicación es distributiva sobre la suma:

(a) Distributivo por la izquierda: ∀ a, b, c ∈ S :

a* ₅ (b + _5c )

= [a * (b + c)] módulo 5

= [a*b + a*c] módulo 5

= (a * ₅ b) +5 (a * ₅ c)

⇒ El módulo 5 de multiplicación es distributivo sobre el módulo 5 de suma.

Del mismo modo, también se puede probar la ley distributiva correcta.

Entonces, podemos concluir que (S,+,*) es un Anillo.

También se pueden dar muchos otros ejemplos en anillos como ( $\mathbb R$ , +, .), ( $\mathbb Q$ , +, .) y así sucesivamente.

Antes de discutir más sobre los anillos, definimos Divisor de cero en un anillo y el concepto de unidad .

Divisor de cero en un anillo:
en un anillo R, se dice que un elemento distinto de cero es divisor de cero si existe un elemento b distinto de cero en R tal que ab=0 o un elemento c distinto de cero en R tal que ca=0 En el primer caso se dice que a es un divisor de cero por la izquierda y en el último caso se dice que es un divisor de cero por la derecha. Obviamente, si R es un anillo conmutativo, entonces si a es un divisor de cero por la izquierda, entonces a también es un divisor de cero por la derecha.

Ejemplo – En el anillo ( $\mathbb Z_6$ , +, .) $\bar{2}, \bar{3}, \bar{4}$ son divisores de cero desde
$\bar{2}.\bar{3}=\bar{6}=\bar{0}$ y así sucesivamente.
Por otro lado los anillos ( $\mathbb Z$ , +, .), ( $\mathbb R$ , +, .), ( $\mathbb Q$ , +, .) no contienen divisor de cero .

Unidades:
en un anillo no trivial R (anillo que contiene al menos dos elementos) con unidad, se dice que un elemento a en R es una unidad si existe un elemento b en R tal que ab = ba = I, siendo I la unidad en R. b se dice que es el inverso multiplicativo de a.

Algunos resultados importantes relacionados con Ring:

Si R es un anillo no trivial (anillo que contiene al menos dos elementos) con unidad I, entonces I 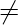$\neq$ 0.
Si I sea una identidad multiplicativa en un anillo R, entonces I es único.
Si a es una unidad en un anillo R entonces su inverso multiplicativo es único.
En un anillo R no trivial, el elemento cero no tiene inverso multiplicativo.

Tipos de anillo:

Anillo nulo : el conjunto singleton: {0} con 2 operaciones binarias ‘+’ y ‘*” definidas por:
0+0 = 0 y 0*0 = 0 se denomina anillo cero/nulo.
Anillo con Unidad : Si existe un elemento en R denotado por 1 tal que :
1*a = a* 1 = a ; ∀ a ∈ R, entonces el anillo se llama Anillo con Unidad.
Anillo conmutativo : si la multiplicación en el anillo R también es conmutativa, entonces el anillo se llama anillo conmutativo.
Anillo de enteros : El conjunto I de enteros con 2 operaciones binarias ‘+’ y ‘*’ se conoce como anillo de enteros.
Anillo booleano : Un anillo en el que cada elemento es idempotente, es decir, a ² = a; ∀ a ∈ R
Ahora introducimos un nuevo concepto de Dominio Integral.

Dominio integral: se dice que un anillo no trivial (anillo que contiene al menos dos elementos) con unidad es un dominio integral si es conmutativo y no contiene divisor de cero.

Ejemplos:
los anillos ( $\mathbb Z$ , +, .), ( $\mathbb R$ , +, .), ( $\mathbb Q$ , +, .) son dominios integrales.
El anillo (2 $\mathbb Z$ , +, .) es un anillo conmutativo pero no contiene la unidad ni divisores de cero. Entonces no es un dominio integral.

A continuación iremos a Campo.

Campo: un anillo no trivial R con unidad es un campo si es conmutativo y cada elemento distinto de cero de R es una unidad. Por lo tanto, un conjunto F no vacío forma un campo .rt dos operaciones binarias + y . si

Para todo a, b $\epsilon$ F, a+b $\epsilon$ F,
Para todo a, b, c $\epsilon$ F a+(b+c)=(a+b)+c,
Existe un elemento en F, denotado por 0 tal que a+0=a para todo un $\epsilon$ F
Para todo a $\epsilon$ R existe un y $\epsilon$ R tal que a+y=0. y generalmente se denota por (-a)
a+b=b+a para todo a, b $\epsilon$ F.
ab $\epsilon$ F para todo ab $\epsilon$ F.
a.(bc)=(ab).c para todo a, b $\epsilon$ F
Existe un elemento I en F, llamado elemento identidad tal que aI=a para todo a en F
Para cada elemento distinto de cero a en F existe un elemento, denotado por 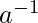$a^{-1}$ en F tal que 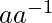$a a^{-1}$ =I.
ab =ba para todo a, b en F .
a.(b+c) =ab + ac para todo a, b, c en F

Ejemplos: los anillos ( $\mathbb Q$ , +, .), ( $\mathbb R$ , + . .) son ejemplos familiares de campos.

Algunos resultados importantes:

Un campo es un dominio integral.
Un dominio integral finito es un campo.
Un anillo conmutativo finito no trivial que no contiene ningún divisor de cero es un dominio integral

Publicación traducida automáticamente

Artículo escrito por tufan_gupta2000 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta