Considere un plano y=f(x) en el plano xy entre las ordenadas x=a y x=b. Si una determinada parte de esta curva gira alrededor de un eje, se genera un sólido de revolución.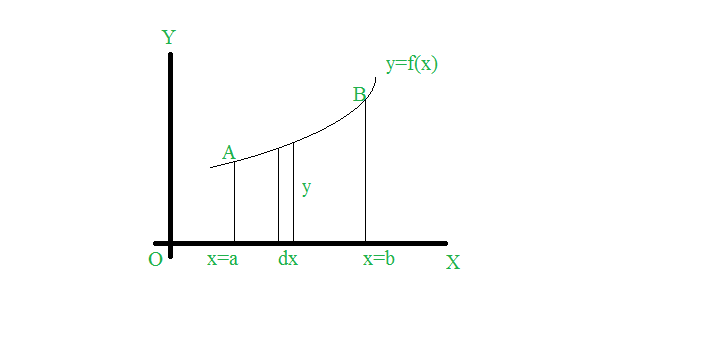
Podemos calcular el área de esta revolución de varias maneras, tales como:
- Forma cartesiana:
- El área del sólido formada al girar el arco de la curva alrededor del eje x es:
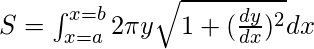
- El área de revolución al girar la curva alrededor del eje y es-
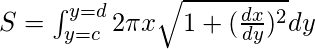
- El área del sólido formada al girar el arco de la curva alrededor del eje x es:
- Forma paramétrica:
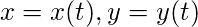
- Sobre el eje x:
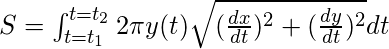
- Sobre el eje y:
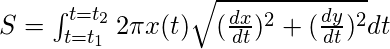
- Sobre el eje x:
- Forma polar: r=f(θ)
- Sobre el eje x: línea inicial
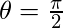
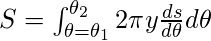
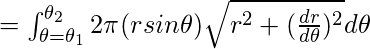
Aquí reemplaza r por f(θ) - Sobre el eje y:
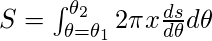
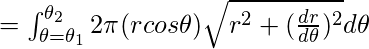
Aquí reemplaza r por f(θ)
- Sobre el eje x: línea inicial
- Sobre cualquier eje o línea L:
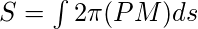 donde PM es la distancia perpendicular de un punto P de la curva al eje dado.
donde PM es la distancia perpendicular de un punto P de la curva al eje dado.
- Límites para x: x = a hasta x = b
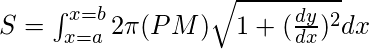
Aquí PM está en términos de x. - Límites para y: y = c a y = d
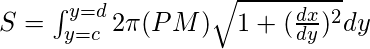
Aquí PM está en términos de y.
- Límites para x: x = a hasta x = b
Ejemplo:
encuentre el área del sólido de revolución generado al girar la parábola ![]() alrededor del eje x.
alrededor del eje x.
Explicación:
Ahora tenemos la forma cartesiana de la ecuación de la parábola y la parábola se ha girado sobre el eje x. Por lo tanto, usamos la fórmula para girar la forma cartesiana sobre el eje x, que es:
![]()
aquí ![]() _ Ahora necesitamos calcular dy/dx
_ Ahora necesitamos calcular dy/dx
Derivando wrt x obtenemos:
![]()
![]()
![]()
Usando![]()
![]()
Ahora contamos con límites de x como x=0 a x=3. Conectando nuestros valores calculados en la fórmula anterior obtenemos:
![]()
![]()
![]()
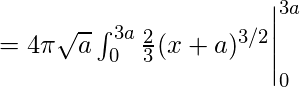
![]()
![]()
![]()