Prerrequisito: Introducción a las Relaciones , Representación de Relaciones
Relaciones combinadas:
Como sabemos que las relaciones son solo conjuntos de pares ordenados, todas las operaciones con conjuntos se aplican a ellos también. Dos relaciones se pueden combinar de varias maneras, tales como:
- Unión:
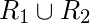 consiste en todos los pares ordenados de ambas relaciones. Pares ordenados duplicados eliminados de Union.
consiste en todos los pares ordenados de ambas relaciones. Pares ordenados duplicados eliminados de Union. - Intersección:
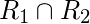 consiste en pares ordenados que están en ambas relaciones.
consiste en pares ordenados que están en ambas relaciones. - Diferencia:
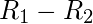 consta de todos los pares ordenados solo en
consta de todos los pares ordenados solo en 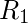 , pero no en
, pero no en 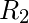 .
. - Diferencia simétrica:
 consiste en todos los pares ordenados que están en
consiste en todos los pares ordenados que están en 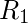 o
o 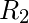 pero no en ambos.
pero no en ambos.
Hay otra manera de combinar dos relaciones que es análoga a la composición de funciones.
Composición – Sea ![]() una relación de
una relación de ![]() a
a ![]() y
y ![]() una relación de
una relación de ![]() a
a ![]() , entonces el compuesto de
, entonces el compuesto de ![]() y
y ![]() , denotado por
, denotado por ![]() , es la relación que consta de pares ordenados
, es la relación que consta de pares ordenados ![]() donde
donde ![]() y para los cuales existe un elemento
y para los cuales existe un elemento ![]() tal que
tal que ![]() y
y ![]() .
.
- Ejemplo: ¿Cuál es el compuesto de las relaciones
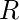 y
y 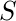 dónde
dónde 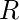 es una relación de
es una relación de 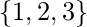 a
a 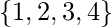 con
con 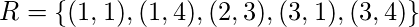 y
y 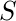 es una relación de
es una relación de 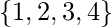 a
a 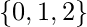 con
con 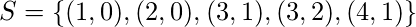 ?
? - Solución: al calcular todos los pares ordenados a los que pertenece el primer elemento
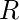 y el segundo elemento
y el segundo elemento 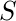 , obtenemos:
, obtenemos: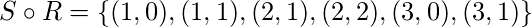
Composición de la Relación sobre sí misma:
Una relación se puede componer consigo misma para obtener un grado de separación entre los elementos del conjunto sobre el que ![]() se define.
se define.
Letbe a relation on the set
. The powers
where
are defined recursively by -
and
.
Teorema – Sea ![]() una relación sobre el conjunto A, representada por un dígrafo. Existe un camino de longitud
una relación sobre el conjunto A, representada por un dígrafo. Existe un camino de longitud ![]() , donde
, donde ![]() es un entero positivo, desde
es un entero positivo, desde ![]() hasta
hasta ![]() si y solo si
si y solo si ![]() .
.
Nota importante: una relación ![]() en conjunto
en conjunto ![]() es transitiva si y solo si
es transitiva si y solo si ![]() para
para![]()
Cierre de Relaciones :
Considere una relación ![]() en el set
en el set ![]() .
. ![]() puede o no tener una propiedad
puede o no tener una propiedad ![]() , como reflexividad, simetría o transitividad.
, como reflexividad, simetría o transitividad.
Si hay una relación ![]() con propiedad
con propiedad ![]() que contiene
que contiene ![]() tal que
tal que ![]() es el subconjunto
es el subconjunto
de toda relación con propiedad ![]() que contiene
que contiene ![]() , entonces
, entonces ![]() se llama cierre de
se llama cierre de ![]() con respecto a
con respecto a ![]() .
.
Podemos obtener cierres de relaciones con respecto a la propiedad ![]() de las siguientes maneras:
de las siguientes maneras:
- Cierre reflexivo:
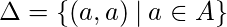 es la relación diagonal en el conjunto
es la relación diagonal en el conjunto 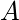 . El cierre reflexivo de la relación
. El cierre reflexivo de la relación 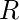 en el set
en el set 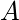 es
es 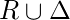 .
. - Cierre simétrico: sea
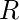 una relación en conjunto
una relación en conjunto 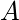 y
y 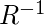 sea la inversa de
sea la inversa de 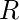 . El cierre simétrico de la relación
. El cierre simétrico de la relación 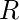 en conjunto
en conjunto 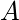 es
es 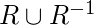 .
. - Cierre transitivo: sea
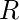 una relación en conjunto
una relación en conjunto 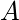 . La relación de conectividad se define como –
. La relación de conectividad se define como – 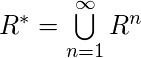 . La clausura transitiva de
. La clausura transitiva de 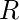 es
es 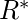 .
.
Ejemplo – Sea ![]() una relación en conjunto
una relación en conjunto ![]() con
con ![]() . Encuentre el cierre reflexivo, simétrico y transitivo de R.
. Encuentre el cierre reflexivo, simétrico y transitivo de R.
Solución –
Para el conjunto dado, ![]() . Entonces el cierre reflexivo de
. Entonces el cierre reflexivo de ![]() es
es![]()
Para el cierre simétrico necesitamos el inverso de ![]() , que es
, que es ![]() .
.
El cierre simétrico de ![]() is-
is-![]()
Para el cierre transitivo, necesitamos encontrar ![]() .
. ![]() tenemos que encontrar
tenemos que encontrar ![]() hasta
hasta ![]() . Nos detenemos cuando se logra esta condición ya que encontrar poderes superiores
. Nos detenemos cuando se logra esta condición ya que encontrar poderes superiores ![]() sería lo mismo.
sería lo mismo. ![]()
![]()
![]()
Ya ![]() que, detenemos el proceso.
que, detenemos el proceso.
Cierre transitivo, ![]() –
–![]()
Relaciones de equivalencia:
Sea ![]() una relación en conjunto
una relación en conjunto ![]() . Si
. Si ![]() es reflexiva, simétrica y transitiva, se dice que es una relación de equivalencia.
es reflexiva, simétrica y transitiva, se dice que es una relación de equivalencia.
En consecuencia, se dice que dos elementos ![]() y
y ![]() relacionados por una relación de equivalencia son equivalentes.
relacionados por una relación de equivalencia son equivalentes.
Ejemplo: demuestre que la relación ![]() es una relación de equivalencia.
es una relación de equivalencia. ![]() es la función módulo de congruencia
es la función módulo de congruencia ![]() . Es verdadero si y sólo si
. Es verdadero si y sólo si ![]() divide
divide ![]() .
.
Solución – Para mostrar que la relación es una relación de equivalencia debemos probar que la relación es reflexiva, simétrica y transitiva.
- Reflexivo: para cualquier elemento
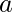 ,
, 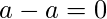 es divisible por
es divisible por 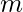 .
. 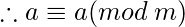 . Entonces, el módulo de congruencia
. Entonces, el módulo de congruencia 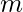 es reflexivo.
es reflexivo. - Simétrico: para dos elementos cualquiera
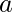 y
y 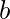 , si
, si 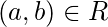 o es
o es 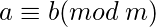 divisible
divisible  por
por 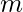 , entonces
, entonces 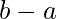 también es divisible por
también es divisible por 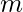 .
. 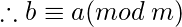 . Entonces el módulo de congruencia
. Entonces el módulo de congruencia 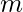 es simétrico.
es simétrico. - Transitiva – Para cualquier tres elementos
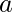 ,
, 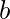 , y
, y 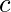 si
si 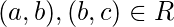 entonces-
entonces- 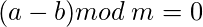
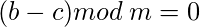
Sumando ambas ecuaciones,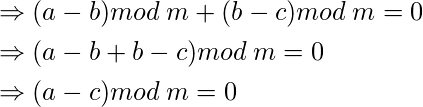
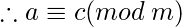 . Entonces,
. Entonces, 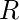 es transitivo.
es transitivo.
Como la relación ![]() es reflexiva, simétrica y transitiva, concluimos que
es reflexiva, simétrica y transitiva, concluimos que ![]() es una relación de equivalencia.
es una relación de equivalencia.
Clases de equivalencia:
Sea ![]() una relación de equivalencia sobre conjunto
una relación de equivalencia sobre conjunto ![]() .
.
Sabemos que si ![]() entonces
entonces ![]() y
y ![]() se dice que son equivalentes con respecto a
se dice que son equivalentes con respecto a ![]() .
.
El conjunto de todos los elementos que están relacionados con un elemento ![]() de
de ![]() se denomina
se denomina
clase de equivalencia de ![]() . Se denota por
. Se denota por ![]() o simplemente
o simplemente ![]() si sólo hay una
si sólo hay una
relación a considerar.
Formalmente,![]()
Se dice que cualquier elemento ![]() es el representante de
es el representante de ![]() .
.
Nota Importante: Todas las clases de equivalencia de una Relación ![]() en conjunto
en conjunto ![]() son iguales o disjuntas y su unión da el conjunto
son iguales o disjuntas y su unión da el conjunto ![]() .
. ![]()
Las clases de equivalencia también se denominan particiones ya que son disjuntas y su unión da el conjunto sobre el que se define la relación.
- Ejemplo: ¿Cuáles son las clases de equivalencia de la relación Módulo de Congruencia
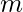 ?
? - Solución: Sean
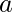 y
y 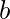 dos números tales que
dos números tales que 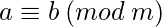 . Esto significa que el resto obtenido al dividir
. Esto significa que el resto obtenido al dividir 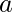 y
y 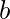 con
con 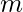 es el mismo.
es el mismo.
Valores posibles para el resto-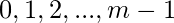
Por lo tanto, hay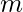 clases de equivalencia-
clases de equivalencia-![Rendered by QuickLaTeX.com [0]_{m}, [1]_{m}, ...,[m-1]_{m}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0a298eb12a6f559bcc05ad1ce6d0703_l3.png)
![Rendered by QuickLaTeX.com [0]_{m} = \{...,-2m, -m, 0, m, 2m,..., \}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0b6d89c2ac06add3f57f5bd1cbb3ff7_l3.png)
![Rendered by QuickLaTeX.com [1]_{m} = \{...,-2m + 1, -m + 1, 1, m + 1, 2m + 1,..., \}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f34ff1e5330531ea058e0c0baad43a7b_l3.png)


![Rendered by QuickLaTeX.com [m-1]_{m} = \{...,-2m - 1, -m - 1 , m - 1, 2m - 1,..., \}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f9daf3826ec95cac6688d296efd19d33_l3.png)
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
1. GATE CS 2013, Pregunta 1
2. GATE CS 2005, Pregunta 42
3. GATE CS 2001, Pregunta 2
4. GATE CS 2000, Pregunta 28
Referencias –
Composición de relaciones – Wikipedia
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen
Este artículo es una contribución de Chirag Manwani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA