Matemáticas | Clases (Inyectiva, Sobreyectiva, Biyectiva) de Funciones

Una función f de A a B es una asignación de exactamente un elemento de B a cada elemento de A (A y B son conjuntos no vacíos). A se llama Dominio de f y B se llama co-dominio de f. Si b es el único elemento de B asignado por la función f al elemento a de A, se escribe como f(a) = b. f asigna A a B. significa que f es una función de A a B, se escribe como

Términos relacionados con las funciones:

• Dominio y codominio : si f es una función del conjunto A al conjunto B, entonces A se llama Dominio y B se llama codominio.
• Rango : el rango de f es el conjunto de todas las imágenes de los elementos de A. Básicamente, el rango es un subconjunto del codominio.
• Imagen y Pre-Imagen – b es la imagen de a y a es la pre-imagen de b si f(a) = b.

Propiedades de la función:

1. Suma y multiplicación: sean f1 y f2 dos funciones de A a B, entonces f1 + f2 y f1.f2 se definen como-:
   f1+f2(x) = f1(x) + f2(x). (suma)
   f1f2(x) = f1(x) f2(x). (multiplicación)
2. Igualdad: dos funciones son iguales solo cuando tienen el mismo dominio, el mismo codominio y los mismos elementos de mapeo de dominio a codominio.

Tipos de funciones:

1. Función uno a uno (Inyectiva): Una función se llama uno a uno si para todos los elementos a y b en A, si f(a) = f(b), entonces debe darse el caso de que a = b. Nunca asigna elementos distintos de su dominio al mismo elemento de su codominio .
   

   Podemos expresar que f es uno a uno usando cuantificadores como 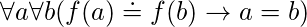o equivalentemente 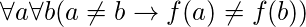, donde el universo de discurso es el dominio de la función.

2. Función Onto (sobreyectiva): Si todo elemento b en B tiene un elemento correspondiente a en A tal que f(a) = b. No se requiere que a sea único; La función f puede mapear uno o más elementos de A al mismo elemento de B.
   
3. Función de correspondencia uno a uno (biyectiva/invertible): una función es una función biyectiva si es una función uno a uno y sobre.

   

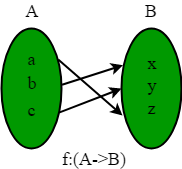
4. Funciones inversas: la función de biyección también se conoce como función invertible porque tienen la propiedad de función inversa. El inverso de la biyección f se denota como f ^-1 . Es una función que asigna a b, un único elemento a tal que f(a) = b. luego f ^-1 (b) = a.

Algunas funciones útiles -:

Funciones estrictamente crecientes y estrictamente decrecientes: Una función f es estrictamente creciente si f(x) > f(y) cuando x>y. Una función f es estrictamente decreciente si f(x) < f(y) cuando x<y.

Funciones crecientes y decrecientes: Una función f es creciente si f(x) ≥ f(y) cuando x>y. Una función f es decreciente si f(x) ≤ f(y) cuando x<y.

Composición de funciones: sea g una función de B a C y f una función de A a B, la composición de f y g, que se denota como fog(a)= f(g(a)).

Propiedades de la composición de funciones:

1. niebla ≠ gof
2. f ^-1 de = f ^-1 (f(a)) = f ^-1 (b) = a.
3. fof ^-1 = f(f ^-1 (b)) = f(a) = b.
4. Si f y g son funciones uno a uno, entonces la niebla también es uno a uno.
5. Si f y g están sobre la función, entonces la niebla también está sobre.
6. Si f y fog son funciones uno a uno, entonces g también es uno a uno.
7. Si f y fog son sobre, entonces no es necesario que g también sea sobre.
8. (niebla) ^-1 = g ^-1 de ^-1

Algunos puntos importantes:

1. Una función es uno a uno si es estrictamente creciente o estrictamente decreciente.
2. La función uno a uno nunca asigna el mismo valor a dos elementos de dominio diferentes.
3. Para la función on, el rango y el codominio son iguales.
4. Si una función f no es biyectiva, no se puede definir la función inversa de f.

Este artículo es una contribución de Nitika Bansal