Matemáticas | Conceptos básicos de combinatoria

La combinatoria es la rama de las Matemáticas que se ocupa del estudio de las estructuras discretas finitas o contables. Incluye la enumeración o conteo de objetos que tienen ciertas propiedades. Contar nos ayuda a resolver varios tipos de problemas, como contar la cantidad de direcciones IPv4 o IPv6 disponibles.

Principios de conteo –

Hay dos principios básicos de conteo, la regla de la suma y la regla del producto.

Regla de la suma: si una tarea se puede realizar de una $n_1$ o varias $n_2$ formas, donde ninguna de las $n_1$ formas es igual a ninguna de las $n_2$ formas, entonces hay $n_1 + n_2$ formas de realizar la tarea.

Regla del producto: si una tarea se puede dividir en una secuencia de $k$ subtareas, donde cada subtarea se puede realizar $n_1, n_2,.. n_k$ respectivamente, entonces la cantidad total de formas en que se puede realizar la tarea es $n_1 * n_2 * ... * n_k$ .

Ejemplo 1: ¿De cuántas maneras se pueden dar 3 premios ganadores a los 3 mejores jugadores en un juego jugado por 12 jugadores?
Solución – Tenemos que repartir 3 premios entre 12 jugadores. Esta tarea se puede dividir en 3 subtareas de asignar un premio único a un jugador determinado.
La entrega del primer premio se puede realizar de 12 formas diferentes. Después de entregar el primer premio, quedan dos premios y quedan 11 jugadores. Del mismo modo, el segundo premio y el tercer premio se pueden otorgar de 11 formas y 10 formas. El número total de vías por la regla del producto es 12 * 11 * 10 = 1320.
Ejemplo 2: ¿De cuántas maneras puede una persona elegir un proyecto de tres listas de proyectos de tamaños 10, 15 y 19 respectivamente?
Solución: la persona tiene la opción de elegir un proyecto de cualquiera de las tres listas. Entonces, la persona puede elegir entre 10 proyectos, 15 proyectos o 19 proyectos. Dado que elegir de una lista no es lo mismo que elegir otra lista, el número total de formas de elegir un proyecto por la regla de la suma es 10 + 15 + 19 = 44.
Ejemplo 3: cuántas placas distintas son posibles en el formato dado: dos alfabetos en mayúsculas, seguidos de dos dígitos, luego un guión y finalmente cuatro dígitos. Muestra-AB12-3456.
Solución: hay 26 posibilidades para cada una de las dos letras y 10 posibilidades para cada uno de los dígitos. Por lo tanto, el número total de posibilidades es: 26 * 26 * 10 * 10 * 10 * 10 * 10 * 10 = 676000000.
Ejemplo 4: ¿cuántos nombres de variables de longitud hasta 3 existen si los nombres de las variables son alfanuméricos y distinguen entre mayúsculas y minúsculas con la restricción de que el primer carácter tiene que ser un alfabeto?
Solución: denote $N_1, N_2, and N_3$ el número de posibles nombres de variables de longitud 1, 2 y 3. Por lo tanto, el número total de nombres de variables es $N_1 + N_2 + N_3$ .
Porque $N_1$ solo hay 52 posibilidades ya que el primer carácter tiene que ser un alfabeto.
Para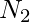 $N_2$ , hay 52 * 62 = 3224 posibilidades
Para $N_3$ , hay 52 * 62 * 62 = 199888 posibilidades
Por lo tanto, número total de nombres de variables = 52 + 3224 + 199888 = 203164

Principio de Inclusión-Exclusión:

La regla de la suma mencionada anteriormente establece que si hay varios conjuntos de formas de realizar una tarea, no debería haber ninguna forma común entre dos conjuntos de formas porque, si la hay, se contaría dos veces y la enumeración sería equivocado.
El principio de inclusión-exclusión dice que para contar solo formas únicas de hacer una tarea, debemos sumar la cantidad de formas de hacerla de una forma y la cantidad de formas de hacerla de otra y luego restar la cantidad de formas. para hacer la tarea que son comunes a ambos conjuntos de formas.
El principio de inclusión-exclusión también se conoce como principio de sustracción . Para dos conjuntos de formas $A_1$ y $A_2$ , la enumeración sería:

Ejemplo 1: ¿cuántas strings binarias de longitud 8 comienzan con un bit ‘1’ o terminan con dos bits ’00’?
Solución: si la string comienza con uno, quedan 7 caracteres que se pueden completar de varias $2^7 = 128$ maneras.
Si la string termina con ’00’, se pueden completar 6 caracteres de varias $2^6 = 64$ formas.
Ahora bien, si sumamos los conjuntos de formas anteriores y concluimos que es la respuesta final, entonces sería incorrecto. Esto se debe a que hay strings que comienzan con ‘1’ y terminan con ’00’, y dado que cumplen ambos criterios, se cuentan dos veces.
Entonces necesitamos restar tales strings para obtener un conteo correcto.
Las strings que comienzan con ‘1’ y terminan con ’00’ tienen cinco caracteres que se pueden completar de varias $2^5 = 32$ maneras.
Por el principio de inclusión-exclusión obtenemos:
Total de strings = 128 + 64 – 32 = 160
Ejemplo 2: ¿Cuántos números entre 1 y 1000, incluidos ambos, son divisibles por 3 o por 4?
Solución – Número de números divisibles por 3 = $|A_1|$ = $\lfloor 1000/3\rfloor = 333$ .
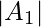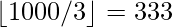Número de números divisibles por 4 =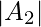 $|A_2|$ = $\lfloor 1000/4\rfloor = 250$ .
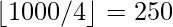Número de números divisibles por 3 y 4 = $|A_1 \cap A_2|$ = $\lfloor 1000/12\rfloor = 83$ .
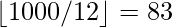Por lo tanto, número de números divisible por 3 o 4 =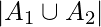 $|A_1 \cup A_2|$ = 333 + 250 – 83 = 500

Preguntas de GATE CS Corner

Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.

1. GATE CS 2007, Pregunta 3
2. GATE CS 2004, Pregunta 26

Encuentra el siguiente artículo @ Principio Pigeonhole

Referencias-

Combinatoria – Wikipedia
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen

Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta