Requisito previo: PnC y coeficientes binomiales
Hasta ahora, todos los problemas discutidos en artículos anteriores han tenido conjuntos de elementos distintos, pero a veces los problemas pueden implicar el uso repetido de elementos. Este artículo cubre tales problemas, donde los elementos del conjunto son indistinguibles (o idénticos o no distintos).
Permutaciones con repetición: el
conteo de permutaciones cuando la repetición de elementos se puede hacer fácilmente usando la regla del producto.
Ejemplo, el número de strings de longitud ![]() es
es ![]() , ya que para cada carácter hay 26 posibilidades.
, ya que para cada carácter hay 26 posibilidades.
The number of-permutations of a set of
objects with repetition is
.
Combinaciones con repetición:
contar el número de combinaciones con repetición es un poco más complicado que contar permutaciones. Considere un conjunto de ![]() tipos de objetos y necesitamos averiguar de cuántas maneras se
tipos de objetos y necesitamos averiguar de cuántas maneras se ![]() pueden elegir los elementos.
pueden elegir los elementos.
Para resolver el problema anterior, primero veremos un problema similar que consiste en organizar barras (|) y estrellas (*). Supongamos que hay 5 barras y 3 estrellas. Un arreglo posible es:
||*||**|
Se pueden organizar de ![]() maneras.
maneras.
Nuestro problema original es similar al problema anterior. Las barras representan divisiones entre los tipos de elementos, de modo que cada tipo está separado por una barra y el número de estrellas es ![]() .
.
Si una estrella está antes de la barra n, significa que se ha seleccionado un elemento de tipo n, excepto el último tipo donde la estrella puede estar después de una barra. Por ejemplo, el arreglo mencionado arriba, ||*||**|, representa una selección de 1 elemento de 3er tipo y 2 elementos de 5to tipo.
De esta forma, nuestro problema original puede pensarse como ordenar ![]() estrellas (elementos) y
estrellas (elementos) y ![]() barras (divisiones). El resultado anterior se puede generalizar como-
barras (divisiones). El resultado anterior se puede generalizar como-
There are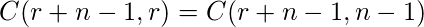
-combinations from a set with
elements when repetition is allowed.
- Ejemplo 1: ¿De cuántas maneras se pueden elegir 4 bebidas de 6 tipos posibles de bebidas? No hay restricción sobre el número de bebidas de un tipo que se puede elegir y las bebidas del mismo tipo son indistinguibles.
- Solución: el escenario anterior es una aplicación directa de encontrar combinaciones con repetición. Así que el número de combinaciones de 4 es –
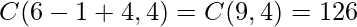 .
.
- Ejemplo 2: ¿Cuántas soluciones tiene la ecuación
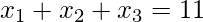 , dónde
, dónde 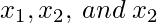 están los números enteros no negativos?
están los números enteros no negativos?
- Solución:
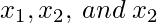 puede tener valores que van de 0 a 11. Esta situación es análoga a encontrar 11 combinaciones de 3 tipos de objetos.
puede tener valores que van de 0 a 11. Esta situación es análoga a encontrar 11 combinaciones de 3 tipos de objetos.
Así que el número de soluciones es –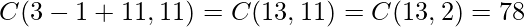
- Ejemplo 3: Considere la misma pregunta que el Ejemplo 2 pero con la restricción adicional de que
 .
.
- Solución: dado que el valor mínimo de
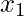 es 1, la ecuación efectiva se convierte en
es 1, la ecuación efectiva se convierte en 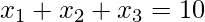 . Entonces el número de soluciones es-
. Entonces el número de soluciones es- 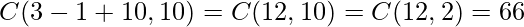
- Ejemplo 4: Considere la misma pregunta que el Ejemplo 2 pero con la restricción adicional de que
 .
.
- Solución: dado que la restricción no es un límite inferior sino un límite superior, no se puede resolver de la misma manera que en el Ejemplo 3. Hay otra forma de resolver este tipo de problemas.
Para cada tipo de objeto asignamos un polinomio de la forma –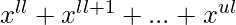 , donde ‘ll’ y ‘ul’ son los límites inferior y superior para ese tipo de objeto.
, donde ‘ll’ y ‘ul’ son los límites inferior y superior para ese tipo de objeto.
Luego, todos esos polinomios se multiplican y el coeficiente de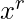 es el número de
es el número de 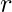 combinaciones.
combinaciones.
En nuestro caso, hay una restricción solo en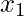 . Por lo tanto, su polinomio es-
. Por lo tanto, su polinomio es- 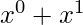
Polinomio para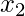 y
y 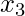 es-
es- 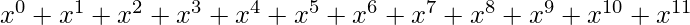
Dado que multiplicar polinomios puede ser tedioso, usamos un truco que usa el teorema del binomio.
El polinomio anterior se puede extender para ser una serie infinita ya que los términos de orden superior no harán ninguna diferencia ya que solo buscamos el coeficiente de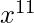 .
.
Así que el polinomio para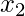 y
y 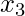 es-
es- 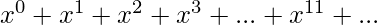
El polinomio anterior también es la expansión para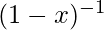 .
.
Al multiplicar los polinomios obtenemos-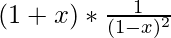
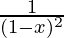 puede expandirse mediante el teorema del binomio para exponentes negativos. No necesitaremos expandir el polinomio completo, ya que solo necesitamos los términos
puede expandirse mediante el teorema del binomio para exponentes negativos. No necesitaremos expandir el polinomio completo, ya que solo necesitamos los términos 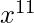 y
y 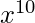 , porque se multiplicarán por 1 y
, porque se multiplicarán por 1 y 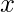 para obtener términos de
para obtener términos de 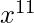 .
. 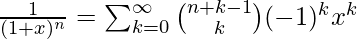 .
.
Para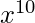 [Tex]k=10 [/Tex], obtenemos-
[Tex]k=10 [/Tex], obtenemos- 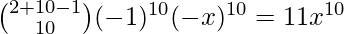
Para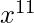 [Tex]k=11 [/Tex], obtenemos-
[Tex]k=11 [/Tex], obtenemos- 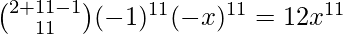
Al multiplicar los términos obtenidos anteriormente por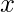 y 1 obtenemos términos de
y 1 obtenemos términos de 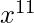 . Al sumarlos obtenemos-
. Al sumarlos obtenemos- 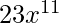 .
.
Por lo tanto, hay 23 soluciones para la ecuación dada.
- Ejemplo 5: considere la misma pregunta que en el Ejemplo 2 pero con una desigualdad, es decir
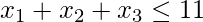 , .
, .
- Solución – Podríamos resolver este problema de 2 maneras.
Una forma es sumar todas las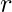 combinaciones para valores
combinaciones para valores 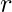 desde 0 hasta 11, es decir ,
desde 0 hasta 11, es decir , 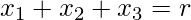 para
para 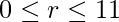 . Obtenemos los siguientes valores :
. Obtenemos los siguientes valores :
For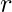 = 0,ways = C(3-1+0,2) = C(2,2) = 1
= 0,ways = C(3-1+0,2) = C(2,2) = 1
For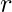 = 1,ways = C(3-1+1,2) = C( 3,2) = 3
= 1,ways = C(3-1+1,2) = C( 3,2) = 3
For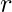 = 2, formas = C(3-1+2,2) = C(4,2) = 6
= 2, formas = C(3-1+2,2) = C(4,2) = 6
For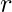 = 3, formas = C(3-1+3,2) = C( 5,2) = 10
= 3, formas = C(3-1+3,2) = C( 5,2) = 10
Para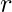 = 4, vías = C(3-1+4,2) = C(6,2) = 15
= 4, vías = C(3-1+4,2) = C(6,2) = 15
Para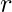 = 5, vías = C(3-1+5,2) = C( 7,2) = 21
= 5, vías = C(3-1+5,2) = C( 7,2) = 21
Para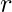 = 6, vías = C(3-1+6,2) = C(8,2) = 28
= 6, vías = C(3-1+6,2) = C(8,2) = 28
Para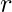 = 7, vías = C(3-1+7,2) = C( 9,2) = 36
= 7, vías = C(3-1+7,2) = C( 9,2) = 36
Para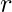 = 8, vías = C(3-1+8,2) = C(10,2) = 45
= 8, vías = C(3-1+8,2) = C(10,2) = 45
Para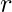 = 9, vías = C(3-1+9,2) = C(11,2) = 55
= 9, vías = C(3-1+9,2) = C(11,2) = 55
Para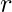 = 10, vías = C(3-1+10,2) = C(12,2) = 66
= 10, vías = C(3-1+10,2) = C(12,2) = 66
Para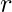 = 11, formas = C(3-1+11,2) = C(13,2) = 78
= 11, formas = C(3-1+11,2) = C(13,2) = 78
Número total de soluciones = 364
El problema anterior es el mismo que encontrar el número de soluciones para la ecuación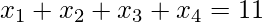
: la variable adicional se puede considerar como la diferencia de 11 y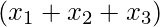 .
.
Cuando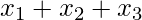 es 0,
es 0, 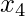 es 11. Por lo que
es 11. Por lo que 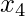 toma valores en consecuencia.
toma valores en consecuencia.
Y el número de soluciones de esta ecuación es – C(4-1+11,4-1) = C(14,3) = 364.
Referencias:
permutaciones y combinaciones
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen
Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA