Requisito previo: PnC generalizado Conjunto 1
Los problemas combinatorios se pueden reformular de varias maneras diferentes, la más común de las cuales es en términos de distribución de bolas en cajas. Así que debemos familiarizarnos con la terminología para poder resolver problemas.
Las bolas y cajas pueden ser distinguibles o indistinguibles y la distribución puede realizarse con exclusión o sin ella .
El término exclusión significa que ninguna caja puede contener más de una bola, y de manera similar, si el problema establece que la distribución es sin exclusión, significa que una caja puede contener más de una bola.
A lo largo de este artículo considere que hay ![]() bolas y
bolas y ![]() cajas.
cajas.
1. Bolas distinguibles y Cajas distinguibles –
Con Exclusión – En caso de exclusión, la distribución es lo mismo que contar ![]() -permutaciones, ya que hay
-permutaciones, ya que hay ![]() opciones para la primera bola,
opciones para la primera bola, ![]() para la segunda y así sucesivamente.
para la segunda y así sucesivamente.
Sin Exclusión – Cuando la distribución es sin exclusión, es decir, no hay restricción en el número mínimo de bolas que debe tener una caja, el número de vías – ![]() . Esto se debe a que cada bola tiene
. Esto se debe a que cada bola tiene ![]() opciones.
opciones.
Número fijo de bolas: si la distribución es tal que cada caja solo debe tener un número fijo de bolas, entonces el número de formas es: ¿ ![]() dónde
dónde ![]() está el número de bolas que se colocarán en la
está el número de bolas que se colocarán en la ![]() caja?
caja?
- Ejemplo 1 – ¿De cuántas formas se pueden repartir 10 premios entre 5 personas sin exclusión?
- Solución: esta situación es análoga a la distribución de bolas distintas en cajas distintas sin exclusión. Por cada premio hay 5 opciones de personas que pueden recibirlo. Así que el número de formas de distribuir los premios es-
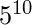 .
. - Ejemplo 2: ¿De cuántas maneras hay de distribuir manos de 5 cartas a cada uno de los cuatro jugadores de una baraja estándar de 52 cartas?
- Solución: esta situación es análoga a la distribución de bolas distintas en cajas distintas donde cada caja debe tener una cierta cantidad de bolas.
La primera persona puede obtener las cartas en formas C(52,5).
La segunda persona puede obtener las cartas en formas C(47,5) y así sucesivamente hasta que la cuarta persona pueda obtener las cartas en formas C(37,5). Después de que se hayan distribuido 20 bolas (cartas), las cartas restantes forman la quinta caja (o jugador).
Esto se puede resolver con la regla del producto, formas totales-
=
=
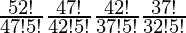
=
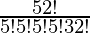
Esto también podría resolverse usando la fórmula mencionada anteriormente usando tamaños de grupo 5,5,5,5 y 32.
2. Bolas indistinguibles y cajas distinguibles –
Contar el número de formas de colocar bolas indistinguibles en cajas distinguibles con exclusión es lo mismo que contar ![]() combinaciones sin repetición de elementos. Pero si la distribución es sin exclusión entonces el problema es el mismo que contar el número de
combinaciones sin repetición de elementos. Pero si la distribución es sin exclusión entonces el problema es el mismo que contar el número de ![]() combinaciones donde los elementos pueden repetirse. Consulte Generalized PnC Part-1 para obtener más información sobre este tema.
combinaciones donde los elementos pueden repetirse. Consulte Generalized PnC Part-1 para obtener más información sobre este tema.
3. Bolas distinguibles y cajas indistinguibles –
No existe una fórmula cerrada simple para contar el número de formas de distribuir bolas distinguibles en cajas indistinguibles, pero existe una fórmula compleja que involucra el número de Stirling del segundo tipo.
El número de Stirling se denota por ![]() donde
donde ![]() es el número de bolas y
es el número de bolas y ![]() es el número de cajas no vacías.
es el número de cajas no vacías. 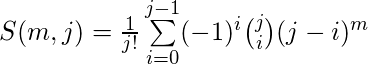
Así que el número de formas es-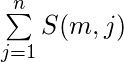
4. Bolas indistinguibles y cajas indistinguibles –
Contar el número de formas de distribuir bolas indistinguibles en objetos indistinguibles es análogo a encontrar el número de particiones de un entero positivo. No existe una fórmula simple para encontrar el número de particiones de un entero positivo.
Para los dos casos anteriores, la enumeración de todas las formas a veces es más fácil que encontrar una fórmula cerrada que dé el mismo resultado.
- Ejemplo 1: ¿Cuántas formas hay de poner cuatro bolas diferentes en tres oficinas indistinguibles sin exclusión?
- Solución: es más fácil enumerar todos los escenarios posibles en lugar de utilizar la fórmula de Stirling. Que sean las cuatro bolas
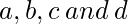 .
.
Todas las pelotas en una caja –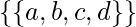
3 pelotas en una caja y 1 en otra –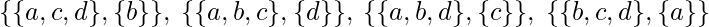
2 pelotas en una caja y 2 en otra –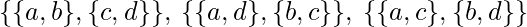
2 pelotas en una caja y 1 en cada una de las cajas restantes –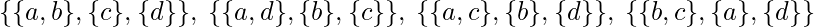
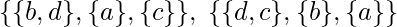
Esto nos da un total de – 1 + 3 + 4 + 6 = 14 vías. - Ejemplo 2: ¿De cuántas maneras hay de poner 4 bolas indistinguibles en 3 cajas indistinguibles?
- Solución: como se mencionó anteriormente, el problema anterior es similar a encontrar el número de particiones del entero positivo 4, donde el número de particiones es menor o igual a 3.
Enumerar todas las formas posibles:
las cuatro bolas en una caja: 4
3 pelotas en una caja, 1 pelota en una – 3,1
2 pelotas en dos cajas – 2,2
2 pelotas en 1 caja, 1 pelota en dos cajas cada una – 2,1,1
Número total de formas = 4
Es similar a encontrar el número de particiones de 4-
4 = 4
3 + 1 = 4
2 + 2 = 4
2 + 1 + 1 = 4
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
Referencias-
Teoría de números de partición – Wikipedia
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen
Este artículo es una contribución de Chirag Manwani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA