El artículo anterior cubrió los conceptos básicos de las Distribuciones de Probabilidad y habló sobre la Distribución de Probabilidad Uniforme . Este artículo cubre la distribución de probabilidad exponencial, que también es una distribución continua al igual que la distribución uniforme.
Introducción –
Supongamos que se nos plantea la pregunta: ¿cuánto tiempo debemos esperar antes de que ocurra un evento determinado?
La respuesta a esta pregunta se puede dar en términos probabilísticos si modelamos el problema dado usando la Distribución Exponencial.
Dado que se desconoce el tiempo que debemos esperar, podemos considerarlo como una variable aleatoria. Si la probabilidad de que ocurra el evento en un intervalo dado es proporcional a la longitud del intervalo, entonces la variable aleatoria tiene una distribución exponencial.
El soporte (conjunto de valores que puede tomar la Variable Aleatoria) de una Variable Aleatoria Exponencial es el conjunto de todos los números reales positivos.![]()
Función de densidad de probabilidad –
Para un número real positivo, ![]() la función de densidad de probabilidad de una variable aleatoria distribuida exponencialmente está dada por:
la función de densidad de probabilidad de una variable aleatoria distribuida exponencialmente está dada por:
![Rendered by QuickLaTeX.com f_X(x) = \[ \begin{cases} \lambda e^{-\lambda x} & if x\in R_X 0 \\ 0 & if x \notin R_X \end{cases} \]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32517ed7821660fed53bac1a26c4c3bc_l3.png)
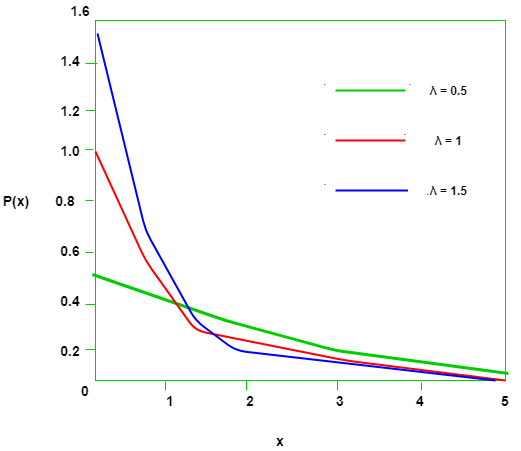
Aquí ![]() está el parámetro de tasa y sus efectos en la función de densidad se ilustran a continuación:
está el parámetro de tasa y sus efectos en la función de densidad se ilustran a continuación:
Para verificar si la función anterior es una función de densidad de probabilidad legítima, debemos verificar si su integral sobre su soporte es 1.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} & = \int\limits_{-\infty}^{\infty} f_X(x) dx \\ & = \int\limits_{0}^{\infty} \lambda e^{-\lambda x} dx \\ & = \frac{\lambda}{-\lambda} \big[ e^{-\lambda x} \big] \limits_{0}^{\infty} \\ & = - \big[ 0 - 1 \big] \\ & = 1 \end{split} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-883b8709d82d1943a87a50e597914524_l3.png)
Función de densidad acumulativa –
Como sabemos, la función de densidad acumulativa no es más que la suma de probabilidad de todos los eventos hasta un cierto valor de ![]() .
.
En la distribución exponencial, la función de densidad acumulada ![]() viene dada por:
viene dada por:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} F(X) &= \int\limits_{0}^{t} \lambda e^{-\lambda x} dx \\ &= \big[ \frac{\lambda e^{-\lambda x}}{-\lambda} \big]\limits_{0}^{t} \\ &= \big[ -e^{-\lambda t} + 1 \big]\\ &= 1 -e^{-\lambda t} \end{split} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-23b988b9e27268bc95f9e1da3afced4d_l3.png)
Valor esperado –
Para averiguar el valor esperado, simplemente multiplicamos la función de distribución de probabilidad con x e integramos sobre todos los valores posibles (soporte).
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} E[X] & = \int\limits_{-\infty}^{\infty} xf_X(x) dx \\ & = \lambda \int\limits_{0}^{\infty} xe^{-\lambda x} dx \\ & = \lambda \Big\{ \big[ x\int e^{-\lambda x} dx\big]\limits_{0}^{\infty} - \big[ \int \frac{d}{dx} x \big(\int e^{-\lambda x} dx\big)dx \big]\limits_{0}^{\infty} \Big\} \\ & = \lambda \Big\{ \big[ x \frac{e^{-\lambda x}}{-\lambda} \big]\limits_{0}^{\infty} - \big[ \int \frac{e^{-\lambda x}}{-\lambda} dx \big]\limits_{0}^{\infty} \Big\} \\ & = \big[ \frac{-x}{e^{\lambda x}} \big]\limits_{0}^{\infty} + \big[ \int e^{-\lambda x} dx \big]\limits_{0}^{\infty} \\ & = \big[ \frac{-x}{e^{\lambda x}} \big]\limits_{0}^{\infty} + \big[ \frac{e^{-\lambda x}}{-\lambda} \big]\limits_{0}^{\infty} \\ & = \big[ 0-0 \big] - \frac{1}{\lambda} \big[ 0-1 \big] \\ & = \frac{1}{\lambda} \end{split} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ac1e4560d895bae0db93ce4b0f80efd_l3.png)
Varianza y desviación estándar –
La varianza de la distribución exponencial viene dada por:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} Var[X] &= E[X^2] - E[X]^2\\ & = \int\limits_{-\infty}^{\infty} x^2f_X(x) dx - \frac{1}{\lambda ^2}\\ & = \lambda \int\limits_{0}^{\infty} x^2 e^{-\lambda x} dx - \frac{1}{\lambda ^2}\\ & = \lambda \Big\{ \big[ x^2\int e^{-\lambda x} dx\big]\limits_{0}^{\infty} - \big[ \int \frac{d}{dx} x^2 \big(\int e^{-\lambda x} dx\big)dx \big]\limits_{0}^{\infty} \Big\} - \frac{1}{\lambda ^2}\\ & = \lambda \Big\{ \big[ x^2 \frac{e^{-\lambda x}}{-\lambda} \big]\limits_{0}^{\infty} - \big[ \int 2x\frac{e^{-\lambda x}}{-\lambda} dx \big]\limits_{0}^{\infty} \Big\} - \frac{1}{\lambda ^2}\\ & = \big[ \frac{-x^2}{e^{\lambda x}} \big]\limits_{0}^{\infty} + \frac{2}{\lambda}\big[ \int xe^{-\lambda x} dx \big]\limits_{0}^{\infty} - \frac{1}{\lambda ^2}\\ & = [0-0] + \frac{2}{\lambda} * \frac{1}{\lambda} - \frac{1}{\lambda ^2} \\ & = \frac{2}{\lambda ^2} - \frac{1}{\lambda ^2}\\ & = \frac{1}{\lambda ^2} \end{split} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8280cb75dd91a92e68a2c330a2c976f_l3.png)
La desviación estándar de la distribución:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \sigma &= \sqrt{Var[X]}\\ &= \sqrt{\frac{1}{\lambda ^2}}\\ &= \frac{1}{\lambda} \end{split} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0d036a8c79a2521568fcac427997568_l3.png)
- Ejemplo: denote con X el tiempo entre las detecciones de una partícula con un contador Geiger y suponga que X tiene una distribución exponencial con E(X) = 1,4 minutos. ¿Cuál es la probabilidad de que detectemos una partícula dentro de los 30 segundos de iniciar el contador?
- Solución: dado que la variable aleatoria (X) que indica el tiempo entre la detección sucesiva de partículas se distribuye exponencialmente, el valor esperado viene dado por:
![Rendered by QuickLaTeX.com E[X] = \frac{1}{\lambda}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-103b880553688441ed492e7f4cd17656_l3.png)

para encontrar la probabilidad de detectar la partícula dentro de los 30 segundos posteriores al inicio del experimento, necesitamos usar la función de densidad acumulativa discutida anteriormente. Convertimos los 30 segundos dados en minutos ya que tenemos nuestro parámetro de tasa en términos de minutos.
Propiedad de falta de memoria –
Ahora considere que en el ejemplo anterior, después de detectar una partícula en la marca de 30 segundos, no se detecta ninguna partícula tres minutos después.
Debido a que hemos estado esperando durante los últimos 3 minutos, creemos que se debe realizar una detección, es decir, la probabilidad de detección de una partícula en los próximos 30 segundos debe ser superior a 0,3. Sin embargo. esto no es cierto para la distribución exponencial. Podemos demostrarlo al encontrar la probabilidad del escenario anterior, que se puede expresar como una probabilidad condicional 
: el hecho de que hayamos esperado tres minutos sin que nos detecten no cambia la probabilidad de que se produzca una detección en los próximos 30 segundos. Por lo tanto, la probabilidad solo depende de la longitud del intervalo considerado.
Referencias –
Distribución Exponencial
Statlect.com
Publicación traducida automáticamente
Artículo escrito por cmkmanwani y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA