Los artículos anteriores hablaron sobre algunas de las distribuciones de probabilidad continua. Este artículo cubre una de las distribuciones que no son continuas sino discretas, a saber, la distribución binomial .
Introducción –
Para comprender la distribución binomial, primero debemos comprender qué es un ensayo de Bernoulli . Un ensayo de Bernoulli es un experimento aleatorio con solo dos resultados posibles . Estos dos resultados generalmente se conocen como Éxito y Fracaso, pero se les puede dar cualquier etiqueta necesaria. Cada ensayo de Bernoulli o experimento aleatorio es independiente del otro.
Por ejemplo, considere el escenario en el que necesitamos encontrar la probabilidad del evento de que aparezca un número par en la tirada del dado.
Si aparece E = número par, entonces 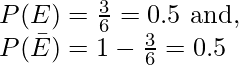
aquí ![]() (o simplemente ‘p’) puede denominarse probabilidad de éxito y
(o simplemente ‘p’) puede denominarse probabilidad de éxito y ![]() (o simplemente ‘q’) puede denominarse probabilidad de fracaso. Darse cuenta de,
(o simplemente ‘q’) puede denominarse probabilidad de fracaso. Darse cuenta de, ![]() , ya que solo hay dos resultados posibles.
, ya que solo hay dos resultados posibles.
Ahora considere que el experimento se repite y tratamos de encontrar la probabilidad de éxito. Obtenemos, ![]()
Esta es la misma probabilidad que el primer experimento. Esto se debe a que los dos experimentos son independientes, es decir, el resultado de un experimento no afecta al otro.
Ahora que sabemos qué es un ensayo de Bernoulli, podemos pasar a comprender la distribución binomial.
A random experiment consists of n Bernoulli trials such that 1. The trials are independent. 2. Each trial results in only two possible outcomes, labeled as “success” and “failure.” 3. The probability of a success in each trial, denoted as p, remains constant. The random variable X that equals the number of trials that result in a success is a binomial random variable with parameters 0 < p < 1 and n = 1, 2, …. The probability mass function is given by-
Función de probabilidad –
La función de masa de probabilidad mencionada anteriormente es una función de probabilidad legítima.
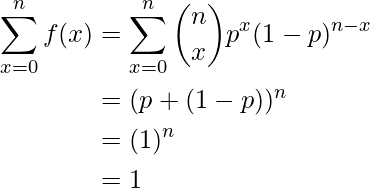
Observe que en la fórmula anterior, si ponemos n=1, obtenemos el mismo resultado que una prueba de Bernoulli. Aquí x puede tomar el valor 0 o 1 (ya que el número de éxitos puede ser 0 o 1 en un experimento). 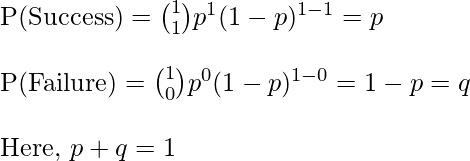
Valor esperado –
Para encontrar el valor esperado de la distribución binomial, primero averigüemos el valor esperado de una prueba de Bernoulli. Sean p y q las probabilidades de éxito (1) y fracaso (0). ![]()
Dado que la distribución binomial tiene n intentos de Bernoulli, el valor esperado se multiplica por n. Esto se debe al hecho de que cada experimento es independiente y el valor esperado de la suma de las variables aleatorias es igual a la suma de sus valores esperados individuales. Esta propiedad también se llama la Linealidad de la Expectativa . ![]()
Varianza y desviación estándar –
La varianza de la distribución Binomial se puede encontrar de manera similar. Para n variables aleatorias independientes,
![]()
Here, Var[BT] is the Variance of 1 Bernoulli trial.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \text{Var[BT]} &= E[X^2] - E[X]^2\\ &= (p*(1^2) + q*(0^2)) - p^2\\ &= p - p^2\\ &= p(1-p)\\ &= pq \end{split} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-99c40ad651e77927ab9d71437a005128_l3.png)
Usando este resultado para averiguar la varianza de la distribución binomial.
La desviación estándar de la distribución-
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \sigma &= \sqrt{Var[X]}\\ &= \sqrt{npq}\\ \end{split} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7ea670579fb089ff20759d331e1a6383_l3.png)
- Ejemplo: una aerolínea vende 65 boletos para un avión con capacidad para 60 pasajeros. Esto se hace porque es posible que algunas personas no se presenten. La probabilidad de que una persona no se presente al vuelo es 0.1. Todos los pasajeros se comportan de forma independiente. Encuentre la probabilidad del evento de que la aerolínea no tenga que organizar boletos separados para el exceso de personas.
- Solución: si se presentan más de 60 personas, la aerolínea debe reprogramar los boletos para el exceso de personas. Sea X la variable aleatoria que denota el número de pasajeros que se presentan. Tenemos que encontrar la probabilidad del evento donde X <=60.
Sea p la probabilidad de que llegue un pasajero. p = 1 – 0,1 = 0,9.
q = 0,1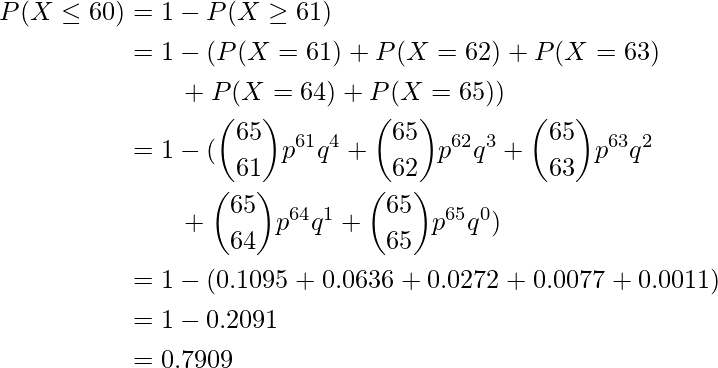
Referencias –
Distribución binomial
Stattrek.com
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA