Un diagrama de Hasse es una representación gráfica de la relación de elementos de un conjunto parcialmente ordenado (poset) con una orientación implícita hacia arriba . Se dibuja un punto para cada elemento del conjunto parcialmente ordenado (poset) y se une con el segmento de línea de acuerdo con las siguientes reglas:
- Si p<q en la pose, entonces el punto correspondiente a p aparece más bajo en el dibujo que el punto correspondiente a q.
- Los dos puntos p y q estarán unidos por un segmento de línea si p está relacionado con q .
Para dibujar un diagrama de Hasse, el conjunto provisto debe ser un poset.
Un poset o conjunto A parcialmente ordenado es un par, (B, ![]() ) de un conjunto B cuyos elementos se denominan vértices de A y obedece a las siguientes reglas:
) de un conjunto B cuyos elementos se denominan vértices de A y obedece a las siguientes reglas:
- Reflexividad → p
 p
p  p
p  B
B - Anti-simétrico → p
 q y q
q y q  p si p=q
p si p=q - Transitividad → si p
 q y q
q y q  r entonces p
r entonces p  r
r
Ejemplo-1: Dibuje el diagrama de Hasse para ({3, 4, 12, 24, 48, 72}, /)
Explicación: primero, de acuerdo con la pregunta anterior, tenemos que encontrar la pose para la divisibilidad.
Sea el conjunto A.
A={(3 ![]() 12), (3
12), (3 ![]() 24), (3
24), (3 ![]() 48), (3
48), (3 ![]() 72), (4
72), (4 ![]() 12), (4
12), (4 ![]() 24), (4
24), (4 ![]() 48), (4
48), (4 ![]() 72), ( 12
72), ( 12 ![]() 24), (12
24), (12 ![]() 48), (12
48), (12 ![]() 72), (24
72), (24 ![]() 48), (24
48), (24 ![]() 72)}
72)}
Entonces, ahora el diagrama de Hasse será:
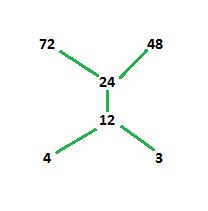
En el diagrama anterior, 3 y 4 están al mismo nivel porque no están relacionados entre sí y son más pequeños que otros elementos del conjunto. El siguiente elemento sucesor de 3 y 4 es 12, es decir, 12 es divisible tanto por 3 como por 4. Luego, 24 es divisible por 3, 4 y 12. Por lo tanto, se coloca por encima de 12. 24 divide tanto a 48 como a 72, pero 48 no. divide 72. Por lo tanto, 48 y 72 no están unidos.
Podemos ver la transitividad en nuestro diagrama a medida que aumenta el nivel.
Ejemplo-2: Dibuje el diagrama de Hasse para (D ![]() , /)
, /)
Explicación: aquí, D ![]() significa un conjunto de números enteros positivos divisores de 12.
significa un conjunto de números enteros positivos divisores de 12.
Entonces, D ![]() ={1, 2, 3, 4, 6, 12}
={1, 2, 3, 4, 6, 12}
poset A = {(1 ![]() 2), (1
2), (1 ![]() 3), (1
3), (1 ![]() 4), (1
4), (1 ![]() 6), (1
6), (1 ![]() 12), (2
12), (2 ![]() 4), (2
4), (2 ![]() 6), (2
6), (2 ![]() 12), (3
12), (3 ![]() 6), (3
6), (3 ![]() 12), (4
12), (4 ![]() 12), (6
12), (6 ![]() 12)}
12)}
Entonces, ahora el Hasse el diagrama sera-
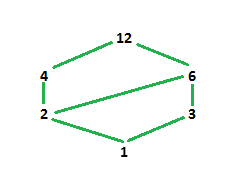
En el diagrama anterior, 1 es el único elemento que divide a todos los demás elementos y es el más pequeño. Por lo tanto, se coloca en la parte inferior. Entonces, los elementos de nuestro conjunto son 2 y 3, que no se dividen entre sí, por lo que se colocan al mismo nivel por separado pero divisibles por 1 (ambos unidos por 1). 4 es divisible por 1 y 2 mientras que 6 es divisible por 1, 2 y 3, por lo tanto, 4 está unido por 2 y 6 está unido por 2 y 3. 12 es divisible por todos los elementos, por lo tanto, unido por 4 y 6 no por todos. elementos porque ya hemos unido 4 y 6 con elementos más pequeños en consecuencia.
Para diagrama de Hasse normal:
- El elemento máximo es un elemento de un POSET que no es menor que cualquier otro elemento del POSET. O podemos decir que es un elemento que no está relacionado con ningún otro elemento. Elementos principales del Diagrama de Hasse.
- Ejemplo: en el diagrama anterior, podemos decir que 4,2,3,6,1 están relacionados con 12 (ordenados por división, por ejemplo, (4, /)), pero 12 no está relacionado con ningún otro. (Ya que el Diagrama de Hasse es direccional hacia arriba).
- Elemento mínimo es un elemento de un POSET que no es mayor que ningún otro elemento del POSET. O podemos decir que ningún otro elemento está relacionado con este elemento. Elementos inferiores del Diagrama de Hasse.
- Ejemplo: en el diagrama anterior, podemos decir que 1 está relacionado con 2,3,4,6,12 (ordenado por división, por ejemplo, (4, /)) pero ningún elemento está relacionado con 1. (Dado que el diagrama de Hasse es direccional hacia arriba ).
- El elemento más grande (si existe) es el elemento que sucede a todos los demás elementos.
- El elemento mínimo es el elemento que precede a todos los demás elementos.
Nota: los elementos mayor y menor en el diagrama de Hasse son solo uno.
En el Ejemplo-1,
los elementos máximos son 48 y 72 ya que suceden a todos los elementos.
Los elementos mínimos son 3 y 4 ya que preceden a todos los elementos.
El elemento más grande no existe ya que no hay ningún elemento que suceda a todos los elementos.
El elemento mínimo no existe ya que no hay ningún elemento que preceda a todos los elementos.
En el Ejemplo-2,
el elemento Máximo y Mayor es 12 y el elemento Mínimo y Mínimo es 1.
NOTA: Un elemento puede ser máximo y mínimo
Ejemplo-

Aquí a,b,c son tanto máximos como mínimos.
Publicación traducida automáticamente
Artículo escrito por Deepanshi_Mittal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA