Requisito previo: generación de funciones: introducción y requisitos previos
En el conjunto 1 llegamos a conocer los conceptos básicos sobre la generación de funciones. Ahora discutiremos más detalles sobre la generación de funciones y sus aplicaciones.
Funciones generadoras exponenciales –
Sea ![]() una secuencia. Entonces su función generadora exponencial, denotada por
una secuencia. Entonces su función generadora exponencial, denotada por ![]() está dada por,
está dada por,
![]()
Ejemplo 1:- Sea {1, 1, 1…….} una secuencia. La función generadora de la secuencia es ![]() ( Aquí
( Aquí ![]() = 1 para todo n )
= 1 para todo n )
Ejemplo 2: – Sea ![]() el número de k permutaciones en un conjunto de n elementos. Entonces la función generadora exponencial para la secuencia
el número de k permutaciones en un conjunto de n elementos. Entonces la función generadora exponencial para la secuencia ![]() es
es
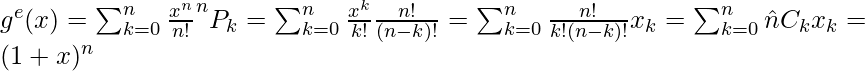
La función de generación exponencial se utiliza para determinar el número de n-permutaciones de un conjunto que contiene elementos repetitivos. Veremos ejemplos más adelante.
Uso de funciones generadoras para resolver relaciones de recurrencia: las relaciones de recurrencia
lineales homogéneas se pueden resolver utilizando la función generadora. Tomaremos un ejemplo aquí para ilustrar.
Ejemplo:- Resuelva la ecuación de recurrencia homogénea lineal ![]() .
.
Dado ![]() =1 y
=1 y ![]() .
.
Usamos la función generadora para resolver este problema. Sea g(x) la función generadora de la sucesión ![]() .
.
Por lo tanto g(x)= ![]()
Entonces obtenemos las siguientes ecuaciones.
g(x)=![]()
-5xg(x)= ![]()
![]() =
=![]()
Sumando estas 3 cantidades obtenemos 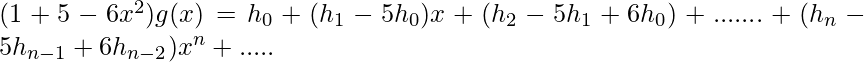
Ahora ![]() =0 para todo n>1. Asi que,
=0 para todo n>1. Asi que,
![]()
O g(x)=![]()
Ahora ![]() =(1-2x)(1-3x)
=(1-2x)(1-3x)
Entonces g(x)=![]()
Es fácil ver eso ![]()
ahora ![]()
y ![]()
Entonces g(x)=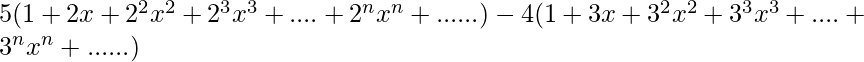
Dado que esta es la función generadora de la sucesión ![]() , observamos que
, observamos que ![]()
Por lo tanto, podemos resolver ecuaciones de recurrencia utilizando funciones generadoras.
Prueba de identidades a través de funciones generadoras:
también se pueden probar varias identidades utilizando funciones generadoras. Aquí ilustramos una de ellas.
Ejemplo: Demostrar que: ![]()
Aquí usamos la función generadora de la secuencia, ![]() es decir
es decir ![]() .
.
Ahora, ![]()
para LHS, el término que contiene ![]() es
es ![]() .Para RHS, el término que contiene
.Para RHS, el término que contiene ![]() es
es ![]() . Entonces
. Entonces ![]() (probado)
(probado)
Los enlaces de varios ejemplos se dan a continuación con respecto a las funciones generadoras.
Publicación traducida automáticamente
Artículo escrito por tufan_gupta2000 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA