Matemáticas | Funciones unimodales y funciones bimodales

Función unimodal:

Una función f(x) se dice que es una función unimodal si para algún valor m es monótonamente creciente para x≤m y monótonamente decreciente para x≥m. Para la función f(x), el valor máximo es f(m) y no hay otro máximo local.
Ver figura (A) y (B):

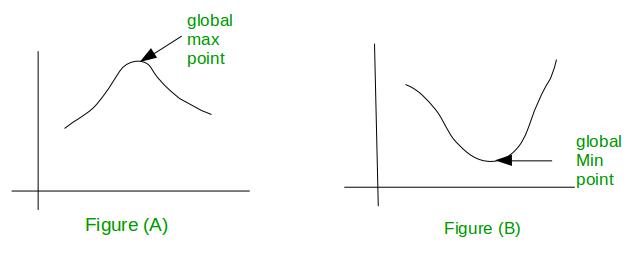
En la figura (A), el gráfico tiene solo un punto máximo y el resto del gráfico desciende desde allí y en la figura (B) el gráfico tiene solo un punto mínimo y el resto del gráfico asciende desde allí. Por lo tanto, podemos decir que si una función tiene un máximo global o un mínimo global, se considera una función unimodal.

Considere una función f(x) en el intervalo [a, b] y tenemos que determinar el valor de x para el cual se maximiza la función. La función crece estrictamente en el intervalo [a, x] y decrece estrictamente en el intervalo [x, b]. Para este propósito, podemos usar la búsqueda binaria modificada para determinar el máximo o el valor de esa función. Haga clic aquí para el programa.

Función bimodal:
se dice que una función es bimodal si tiene dos mínimos o máximos locales. Generalmente la función bimodal indica dos grupos diferentes. Por ejemplo, en una clase hay muchos estudiantes que obtienen una calificación A y muchos que obtienen una calificación D. Esto nos dice que en una clase hay dos grupos diferentes de estudiantes, un grupo está poco preparado y otro grupo está demasiado preparado. Vea esta figura para una mejor comprensión:

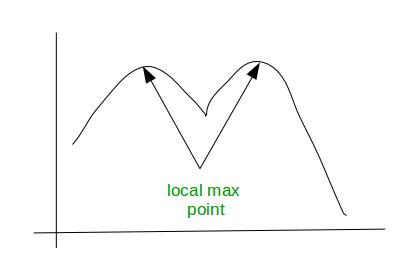
Nota –

• Con la función bimodal y superiores, no sabemos si un extremo es local o global a menos que conozcamos el gráfico completo.
• Con la función unimodal, se garantiza que cualquier extremo que encontremos sea el extremo global.