Prerrequisito: fundamentos de la teoría de grafos
Considere un circuito electrónico que tiene varios Nodes con conexiones entre ellos. ¿Es posible imprimir ese circuito en una sola placa de modo que ninguna de las conexiones se cruce entre sí, es decir, no se superpongan ni se crucen?
Esta pregunta se puede responder si conocemos la planaridad de los gráficos.
Planaridad: “Se dice que un gráfico es plano si se puede dibujar en un plano sin que se crucen los bordes . Tal dibujo se llama representación plana del gráfico”.
Nota importante: un gráfico puede ser plano incluso si se dibuja con cruces, porque es posible dibujarlo de una manera diferente sin cruces.
Por ejemplo, considere el gráfico completo ![]() y sus dos posibles representaciones planas:
y sus dos posibles representaciones planas: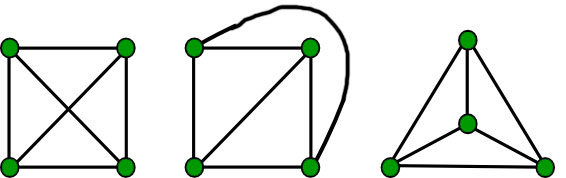
- Ejemplo: ¿el hipercubo es
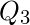 plano?
plano?
- Solución – Sí,
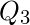 es plana. Su representación plana-
es plana. Su representación plana-
Regiones en Gráficos Planares –
La representación plana de un gráfico divide el plano en regiones . Estas regiones están delimitadas por los bordes excepto por una región que no está delimitada. Por ejemplo, considere el siguiente gráfico » 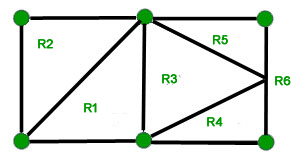
Hay un total de 6 regiones con 5 regiones limitadas y 1 región ilimitada » ![]() .
.
Todas las representaciones planares de un gráfico dividen el plano en el mismo número de regiones. Euler descubrió el número de regiones en un gráfico plano en función del número de vértices y el número de aristas en el gráfico.
Teorema – “Sea ![]() un grafo plano simple conexo con
un grafo plano simple conexo con ![]() aristas y
aristas y ![]() vértices. Entonces el número de regiones
vértices. Entonces el número de regiones ![]() en el gráfico es igual a
en el gráfico es igual a ![]()
donde k es el no. de componente en el gráfico. .”
- Ejemplo: ¿Cuál es el número de regiones en un gráfico simple plano conectado con 20 vértices cada uno con un grado de 3?
- Solución – Suma de grados de aristas = 20 * 3 = 60. Por el teorema del apretón de manos,
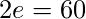 lo que da
lo que da 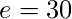 .
.
Por el teorema de Euler, el número de regiones =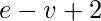 lo que da 12 regiones.
lo que da 12 regiones.
Un resultado importante obtenido por la fórmula de Euler es la siguiente desigualdad:
Nota – “Si ![]() es un grafo plano conexo con
es un grafo plano conexo con ![]() aristas y
aristas y ![]() vértices, donde
vértices, donde ![]() , entonces
, entonces ![]() . Tampoco
. Tampoco ![]() puede tener un vértice de grado superior a 5.”
puede tener un vértice de grado superior a 5.”
- Ejemplo: ¿el gráfico es
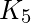 plano?
plano? - Solución: el número de vértices y aristas
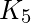 es 5 y 10 respectivamente. Como 10 > 3*5 – 6, 10 > 9, la desigualdad
es 5 y 10 respectivamente. Como 10 > 3*5 – 6, 10 > 9, la desigualdad 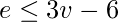 no se cumple. Por lo tanto, el gráfico no es plano.
no se cumple. Por lo tanto, el gráfico no es plano.
Gráfico para colorear –
Si alguna vez decide crear un mapa y necesita colorear las partes de manera óptima, siéntase afortunado porque la teoría de grafos está a su lado. ¿Cuál es el número máximo de colores necesarios para colorear las regiones de un mapa? Esta pregunta junto con otras similares han generado muchos resultados en la teoría de grafos.
Primero, definamos la restricción de colorear de una manera formal:
Colorear: «La coloración de un gráfico simple es la asignación de un color a cada vértice del gráfico de modo que no se asignen dos vértices adyacentes del mismo color».
Una solución simple a este problema es colorear cada vértice con un color diferente para obtener un total de ![]() colores. Pero en algunos casos, el número real de colores requerido podría ser menor.
colores. Pero en algunos casos, el número real de colores requerido podría ser menor.
número cromático: “El menor número de colores necesarios para colorear un gráfico se denomina número cromático . Se denota por ![]() .”
.”
Para los gráficos planos, encontrar el número cromático es el mismo problema que encontrar el número mínimo de colores necesarios para colorear un gráfico plano.
Teorema de los 4 colores: «El número cromático de un gráfico plano no es mayor que 4».
- Ejemplo 1 – ¿Cuál es el número cromático de las siguientes gráficas?
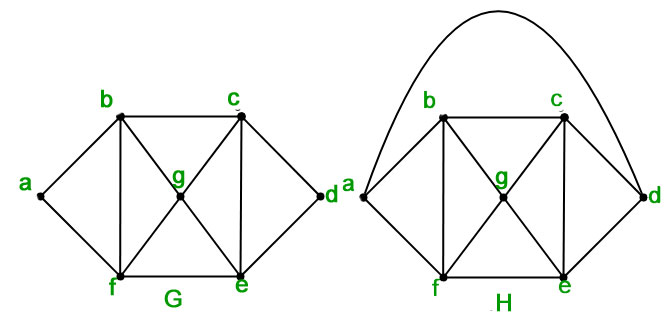
- Solución: en el gráfico
 , el número cromático es al menos tres, ya que los vértices
, el número cromático es al menos tres, ya que los vértices  ,
, 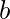 y
y 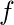 están conectados entre sí.
están conectados entre sí.
La siguiente asignación de color satisface la restricción de color –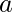 – Rojo
– Rojo 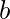 – Verde
– Verde 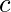 – Azul
– Azul 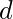 – Rojo
– Rojo 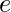 – Verde
– Verde 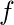 – Azul
– Azul 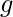 – Rojo
– Rojo
Por lo tanto, el número cromático de es 3.
es 3.
En el gráfico,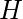 ya que
ya que 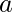 y
y 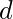 también están conectados, por lo tanto, el número cromático es 4.
también están conectados, por lo tanto, el número cromático es 4. - Ejemplo 2 – ¿Cuál es el número cromático de
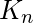 ?
? - Solución: dado que cada vértice está conectado con todos los demás vértices en un gráfico completo, el número cromático es
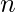 .
. - Ejemplo 3 – ¿Cuál es el número cromático de
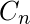 ?
? - Solución: si los vértices están coloreados de forma alterna, el gráfico de ciclo requiere 2 colores. Si
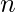 es impar, el último vértice tendrá el mismo color que el primero, por lo que el número cromático será 3. Pero si es par, el primer y el último vértice serán de diferente color y el número cromático será 2.
es impar, el último vértice tendrá el mismo color que el primero, por lo que el número cromático será 3. Pero si es par, el primer y el último vértice serán de diferente color y el número cromático será 2. - Ejemplo 4 – ¿Cuál es el número cromático de
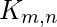 ?
? - Solución: en el gráfico bipartito
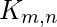 , los vértices en se dividen en dos conjuntos, de modo que no hay borde entre los vértices en el mismo conjunto. Por lo tanto, el número cromático de cualquier gráfico bipartito es 2. A un conjunto de vértices se le puede asignar un color y al otro se le puede asignar un color diferente para un total de 2 colores. Satisfará la restricción de color ya que los vértices del mismo conjunto no están conectados.
, los vértices en se dividen en dos conjuntos, de modo que no hay borde entre los vértices en el mismo conjunto. Por lo tanto, el número cromático de cualquier gráfico bipartito es 2. A un conjunto de vértices se le puede asignar un color y al otro se le puede asignar un color diferente para un total de 2 colores. Satisfará la restricción de color ya que los vértices del mismo conjunto no están conectados.
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
1. GATE CS 2012, Pregunta 21
2. GATE CS 2011, Pregunta 17
3. GATE CS 2009, Pregunta 2
4. GATE CS 2008, Pregunta 23
5. GATE CS 2005 Pregunta 10
6. GATE CS 2005, Pregunta 47
7. GATE CS 2004, Pregunta 77
8. GATE CS 2002, Pregunta 4
9. GATE CS 2015 Conjunto-1, Pregunta 63
10. GATE CS 2008, Pregunta 3
11. GATE CS 2016 Conjunto-2, Pregunta 13
Referencias-
Gráficos planares –
Coloración de gráficos de Wikipedia –
Matemáticas discretas de Wikipedia y sus aplicaciones, por Kenneth H Rosen
Este artículo es una contribución de Chirag Manwani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA