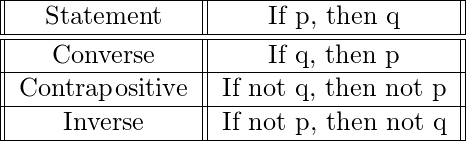Prerrequisito: Introducción a la Lógica Proposicional – Conjunto 1
Ley de De Morgan:
En lógica proposicional y álgebra booleana, las leyes de De Morgan son un par de reglas de transformación que son reglas de inferencia válidas . Llevan el nombre de Augustus De Morgan, un matemático británico del siglo XIX. Las reglas permiten la expresión de conjunciones y disyunciones puramente en términos mutuos a través de la negación.
En lenguaje formal, las reglas se escriben como:
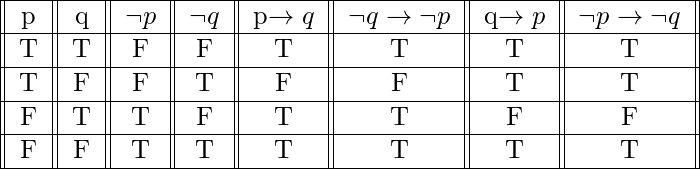
Prueba por tabla de verdad –
Declaraciones condicionales especiales:
Como sabemos, podemos formar nuevas proposiciones usando proposiciones existentes y conectores lógicos. Se pueden formar nuevas sentencias condicionales a partir de una sentencia condicional ![]() .
.
En particular, hay tres declaraciones condicionales relacionadas que ocurren con tanta frecuencia que tienen nombres especiales.
- Implicación :
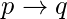
- Recíproco: El recíproco de la proposición
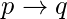 es
es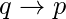
- Contrapositiva : La contrapositiva de la proposición
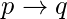 es
es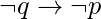
- Inversa: La inversa de la proposición
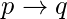 es
es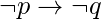
Resumir,
Nota: Es interesante notar que el valor de verdad del enunciado condicional ![]() es el mismo que su contrapositivo, y el valor de verdad del Inverso de
es el mismo que su contrapositivo, y el valor de verdad del Inverso de ![]() es el mismo que el valor de verdad de su Inverso.
es el mismo que el valor de verdad de su Inverso.
Cuando dos proposiciones compuestas tienen siempre el mismo valor de verdad, se dice que son equivalentes.
Por lo tanto,
Ejemplo :
Implicación: si hoy es viernes, entonces está lloviendo.
La proposición dada es de la forma ![]() , donde
, donde ![]() es “Hoy es viernes” y
es “Hoy es viernes” y ![]() es “Hoy está lloviendo”.
es “Hoy está lloviendo”.
Contrapositivo, Converso e Inverso de la proposición dada respectivamente son-
- Converse: Si está lloviendo, entonces hoy es viernes.
- Contrapositivo: Si no llueve, entonces hoy no es viernes.
- Inversa: Si hoy no es viernes, entonces no llueve
Uso implícito de bicondicionales:
El último artículo, la primera parte de este tema, terminó con una discusión sobre los bicondicionales, qué es y su tabla de verdad. En Natural Language, los bicondicionales no siempre son explícitos. En particular, la construcción iff (si y solo si) rara vez se usa en el lenguaje común. En cambio, los bicondicionales a menudo se expresan usando la construcción «si, entonces» o «solo si». La otra parte del “si y sólo si” está implícita, es decir, lo contrario está implícito pero no declarado.
Por ejemplo, considere la siguiente declaración,
“Si completas tu tarea, entonces puedes salir a jugar”. Lo que realmente quiere decir es «Puedes salir y jugar si y solo si completas tu tarea». Esta declaración es lógicamente equivalente a dos declaraciones, «Si completas tu tarea, entonces puedes salir a jugar» y «Puedes salir y jugar solo si completas tu tarea».
Debido a esta imprecisión en el lenguaje natural, se debe suponer si una declaración condicional en lenguaje natural incluye o no su recíproco.
Orden de precedencia de los conectores lógicos:
Los conectores lógicos se utilizan para construir proposiciones compuestas uniendo proposiciones existentes. Aunque se pueden usar paréntesis para especificar el orden en que se deben aplicar los operadores lógicos en la proposición compuesta, existe un orden de precedencia en los operadores lógicos.
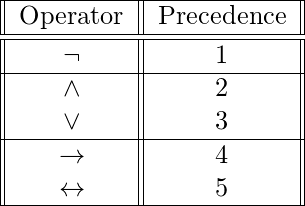
El orden de precedencia es-
Aquí, cuanto mayor sea el número, menor será la precedencia.
Traducción de oraciones en inglés:
Como se mencionó anteriormente en este artículo, los lenguajes naturales como el inglés son ambiguos, es decir, una declaración puede tener múltiples interpretaciones. Por lo tanto, es importante convertir estas oraciones en expresiones matemáticas que involucren variables proposicionales y conectores lógicos.
El proceso de conversión anterior puede tomar ciertas suposiciones razonables sobre el significado pretendido de la oración. Una vez que las oraciones se traducen a expresiones lógicas, se pueden analizar más a fondo para determinar sus valores de verdad. Luego, las reglas de inferencia se pueden usar para razonar sobre las expresiones.
Ejemplo :
“Puede acceder a Internet desde el campus solo si tiene una especialización en informática o no es un estudiante de primer año”.
La declaración anterior podría considerarse como una sola proposición, pero sería más útil dividirla en proposiciones más simples. Eso haría más fácil analizar su significado y razonar con él.
La oración anterior podría dividirse en tres proposiciones,
- "You can access the Internet from campus."
- "You are a computer science major."
- "You are a freshman."
Usando conectores lógicos podemos unir las proposiciones mencionadas anteriormente para obtener una expresión lógica de la declaración dada.
«solo si» es una forma de expresar una declaración condicional (como se discutió en la Parte 1 de este tema en el artículo anterior),
por lo tanto, la expresión lógica sería:
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
1. GATE CS 2009, Pregunta 24
2. GATE CS 2014 Conjunto-1, Pregunta 63
3. GATE CS 2006, Pregunta 28
4. GATE CS 2002, Pregunta 8
5. GATE CS 2000, Pregunta 30
6. GATE CS 2015 Conjunto- 1, Pregunta 24
Referencias –
Lógica proposicional – Wikipedia
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen
Este artículo es una contribución de Chirag Manwani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA