¿Qué es la lógica?
La lógica es la base de todo razonamiento matemático y de todo razonamiento automatizado. Las reglas de la lógica especifican el significado de los enunciados matemáticos. Estas reglas nos ayudan a comprender y razonar con afirmaciones como:
such that
where
Que en Inglés Simple significa “Existe un número entero que no es la suma de dos cuadrados”. Importancia de la lógica matemática Las reglas de la lógica dan un significado preciso a los enunciados matemáticos. Estas reglas se utilizan para distinguir entre argumentos matemáticos válidos e inválidos. Además de su importancia en la comprensión del razonamiento matemático, la lógica tiene numerosas aplicaciones en Ciencias de la Computación, que van desde el diseño de circuitos digitales hasta la construcción de programas de computadora y la verificación de la corrección de los programas.
Lógica proposicional
¿Qué es una proposición? Una proposición es el componente básico de la lógica. Se define como una oración declarativa que es verdadera o falsa, pero no ambas. El valor de verdad de una proposición es Verdadero (denotado como T) si es una afirmación verdadera, y Falso (denotado como F) si es una afirmación falsa. Por ejemplo,
1. The sun rises in the East and sets in the West. 2. 1 + 1 = 2 3. 'b' is a vowel.
Todas las oraciones anteriores son proposiciones, donde las dos primeras son Válidas (Verdaderas) y la tercera es Inválida (Falsa). Algunas oraciones que no tienen un valor de verdad o pueden tener más de un valor de verdad no son proposiciones. Por ejemplo,
1. What time is it? 2. Go out and play. 3. x + 1 = 2.
Las oraciones anteriores no son proposiciones ya que las dos primeras no tienen valor de verdad y la tercera puede ser verdadera o falsa. Para representar proposiciones se utilizan variables proposicionales . Por convención, estas variables se representan con letras pequeñas como ![]() . El área de la lógica que se ocupa de las proposiciones se denomina cálculo proposicional o lógica proposicional . También incluye la producción de nuevas propuestas utilizando las existentes. Las proposiciones construidas usando una o más proposiciones se llaman proposiciones compuestas . Las proposiciones se combinan juntas usando Conectivos Lógicos u Operadores Lógicos .
. El área de la lógica que se ocupa de las proposiciones se denomina cálculo proposicional o lógica proposicional . También incluye la producción de nuevas propuestas utilizando las existentes. Las proposiciones construidas usando una o más proposiciones se llaman proposiciones compuestas . Las proposiciones se combinan juntas usando Conectivos Lógicos u Operadores Lógicos .
Mesa de la verdad
Dado que necesitamos conocer el valor de verdad de una proposición en todos los escenarios posibles, consideramos todas las combinaciones posibles de las proposiciones que se unen mediante conectores lógicos para formar la proposición compuesta dada. Esta compilación de todos los escenarios posibles en un formato tabular se llama tabla de verdad . Conectores lógicos más comunes-
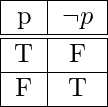
1. Negación: si ![]() es una proposición, entonces la negación de
es una proposición, entonces la negación de ![]() se denota por
se denota por ![]() , que cuando se traduce al inglés simple significa: «No es el caso que
, que cuando se traduce al inglés simple significa: «No es el caso que ![]() » o simplemente «no
» o simplemente «no ![]() «. El valor de verdad de
«. El valor de verdad de ![]() es el opuesto del valor de verdad de
es el opuesto del valor de verdad de ![]() . La tabla de verdad de
. La tabla de verdad de ![]() es-
es-
Ejemplo, La negación de “Hoy llueve”, es “No se da el caso de que hoy llueva” o simplemente “Hoy no llueve”.
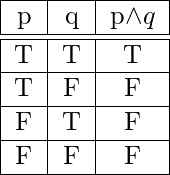
2. Conjunción – Para dos proposiciones cualesquiera ![]() y
y ![]() , su conjunción se denota por
, su conjunción se denota por ![]() , que significa “
, que significa “ ![]() y
y ![]() ”. La conjunción
”. La conjunción ![]() es Verdadera cuando ambos
es Verdadera cuando ambos ![]() y
y ![]() son Verdaderos, de lo contrario Falsa. La tabla de verdad de
son Verdaderos, de lo contrario Falsa. La tabla de verdad de ![]() es-
es-
Ejemplo, la conjunción de las proposiciones ![]() – “Hoy es viernes” y
– “Hoy es viernes” y ![]() – “Hoy está lloviendo”,
– “Hoy está lloviendo”, ![]() es “Hoy es viernes y está lloviendo hoy”. Esta proposición es verdadera solo los viernes lluviosos y es falsa cualquier otro día lluvioso o los viernes cuando no llueve.
es “Hoy es viernes y está lloviendo hoy”. Esta proposición es verdadera solo los viernes lluviosos y es falsa cualquier otro día lluvioso o los viernes cuando no llueve.
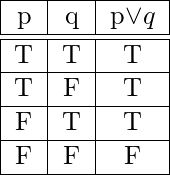
3. Disyunción – Para cualesquiera dos proposiciones ![]() y
y ![]() , su disyunción se denota por
, su disyunción se denota por ![]() , que significa “
, que significa “ ![]() o
o ![]() ”. La disyunción
”. La disyunción ![]() es verdadera cuando
es verdadera cuando ![]() o
o ![]() es verdadera, de lo contrario es falsa. La tabla de verdad de
es verdadera, de lo contrario es falsa. La tabla de verdad de ![]() es-
es-
Ejemplo, la disyunción de las proposiciones ![]() – “Hoy es viernes” y
– “Hoy es viernes” y ![]() – “Hoy está lloviendo”,
– “Hoy está lloviendo”, ![]() es “Hoy es viernes o está lloviendo hoy”. Esta proposición es verdadera en cualquier día que sea viernes o día lluvioso (incluidos los viernes lluviosos) y es falsa en cualquier día que no sea viernes cuando tampoco llueva.
es “Hoy es viernes o está lloviendo hoy”. Esta proposición es verdadera en cualquier día que sea viernes o día lluvioso (incluidos los viernes lluviosos) y es falsa en cualquier día que no sea viernes cuando tampoco llueva.
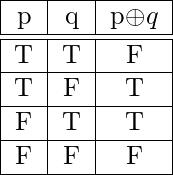
4. O exclusivo: para dos proposiciones cualquiera ![]() y
y ![]() , su o exclusivo se denota por
, su o exclusivo se denota por ![]() , que significa » o una
, que significa » o una ![]() o
o ![]() ambas». El o exclusivo
ambas». El o exclusivo ![]() es Verdadero cuando
es Verdadero cuando ![]() o
o ![]() es Verdadero, y Falso cuando ambos son verdaderos o ambos son falsos. La tabla de verdad de
es Verdadero, y Falso cuando ambos son verdaderos o ambos son falsos. La tabla de verdad de ![]() es-
es-
Ejemplo, El o exclusivo de las proposiciones ![]() – “Hoy es viernes” y
– “Hoy es viernes” y ![]() – “Hoy está lloviendo”,
– “Hoy está lloviendo”, ![]() es “Hoy es viernes o está lloviendo hoy, pero no ambos”. Esta proposición es verdadera en cualquier día que sea viernes o día lluvioso (sin incluir los viernes lluviosos) y es falsa en cualquier día que no sea viernes cuando no llueva o llueva los viernes.
es “Hoy es viernes o está lloviendo hoy, pero no ambos”. Esta proposición es verdadera en cualquier día que sea viernes o día lluvioso (sin incluir los viernes lluviosos) y es falsa en cualquier día que no sea viernes cuando no llueva o llueva los viernes.
5. Implicación – Para cualquiera de las dos proposiciones ![]() y
y ![]() , la afirmación “si
, la afirmación “si ![]() entonces
entonces ![]() ” se llama implicación y se denota por
” se llama implicación y se denota por ![]() . A la implicación
. A la implicación ![]() ,
, ![]() se le llama hipótesis o antecedente o premisa y
se le llama hipótesis o antecedente o premisa y ![]() se le llama conclusión o consecuencia . La implicación
se le llama conclusión o consecuencia . La implicación ![]() también se llama declaración condicional . La implicación es falsa cuando
también se llama declaración condicional . La implicación es falsa cuando ![]() es verdadera y
es verdadera y ![]() es falsa en caso contrario es verdadera. La tabla de verdad de
es falsa en caso contrario es verdadera. La tabla de verdad de ![]() es-
es-
Quizás te preguntes por qué es ![]() cierto cuando
cierto cuando ![]() es falso. Esto se debe a que la implicación garantiza que cuando
es falso. Esto se debe a que la implicación garantiza que cuando ![]() y
y ![]() son verdaderos, entonces la implicación es verdadera. Pero la implicación no garantiza nada cuando la premisa
son verdaderos, entonces la implicación es verdadera. Pero la implicación no garantiza nada cuando la premisa ![]() es falsa. No hay forma de saber si la implicación es falsa o no, ya
es falsa. No hay forma de saber si la implicación es falsa o no, ya ![]() que no sucedió. Esta situación es similar a la postura “inocente hasta que se demuestre lo contrario”, lo que significa que la implicación
que no sucedió. Esta situación es similar a la postura “inocente hasta que se demuestre lo contrario”, lo que significa que la implicación ![]() se considera verdadera hasta que se demuestre lo contrario. Como no podemos llamar falsa a la implicación
se considera verdadera hasta que se demuestre lo contrario. Como no podemos llamar falsa a la implicación ![]() cuando
cuando ![]() es falsa, nuestra única alternativa es llamarla verdadera. Esto se sigue del principio de explosión.que dice: «Una declaración falsa implica cualquier cosa». Las declaraciones condicionales juegan un papel muy importante en el razonamiento matemático, por lo que se usa una variedad de terminología para expresar
es falsa, nuestra única alternativa es llamarla verdadera. Esto se sigue del principio de explosión.que dice: «Una declaración falsa implica cualquier cosa». Las declaraciones condicionales juegan un papel muy importante en el razonamiento matemático, por lo que se usa una variedad de terminología para expresar ![]() , algunas de las cuales se enumeran a continuación.
, algunas de las cuales se enumeran a continuación.
"if, then
""
is sufficient for
""
when
""a necessary condition for
is
""
only if
""
unless
""
follows from
"
Ejemplo: “Si es viernes, hoy llueve” es una proposición de la forma ![]() . La proposición anterior es verdadera si no es viernes (la premisa es falsa) o si es viernes y llueve, y es falsa si es viernes pero no llueve.
. La proposición anterior es verdadera si no es viernes (la premisa es falsa) o si es viernes y llueve, y es falsa si es viernes pero no llueve.
6. Implicación bicondicional o doble: para dos proposiciones cualquiera ![]() y
y ![]() , la declaración »
, la declaración » ![]() si y solo si (si)
si y solo si (si) ![]() » se denomina bicondicional y se denota por
» se denomina bicondicional y se denota por ![]() . La declaración
. La declaración ![]() también se llama bi-implicación .
también se llama bi-implicación . ![]() tiene el mismo valor de verdad que
tiene el mismo valor de verdad que ![]() La implicación es verdadera cuando
La implicación es verdadera cuando ![]() y
y ![]() tienen los mismos valores de verdad, y es falsa en caso contrario. La tabla de verdad de
tienen los mismos valores de verdad, y es falsa en caso contrario. La tabla de verdad de ![]() es-
es-
Algunas otras formas comunes de expresar ![]() son:
son:
"is necessary and sufficient for
""if
then
, and conversely""
iff
"
Ejemplo, “Hoy está lloviendo si y solo si hoy es viernes”. es una proposición que es de la forma ![]() . La proposición anterior es verdadera si no es viernes y no llueve o si es viernes y llueve, y es falsa cuando no es viernes o no llueve. Ejercicio:
. La proposición anterior es verdadera si no es viernes y no llueve o si es viernes y llueve, y es falsa cuando no es viernes o no llueve. Ejercicio:
1) Considere las siguientes afirmaciones:
P: Good mobile phones are not cheap. Q: Cheap mobile phones are not good. L: P implies Q M: Q implies P N: P is equivalent to Q
¿Cuál de los siguientes sobre L, M y N es CORRECTO? (Gate 2014)
(A) Solo L es VERDADERO.
(B) Solo M es VERDADERO.
(C) Solo N es VERDADERO.
(D) L, M y N son VERDADERAS.
Para obtener una solución, consulte GATE | GATE-CS-2014-(Conjunto-3) | Pregunta 11
2) ¿Cuál de los siguientes no es equivalente a p⇔q (Gate 2015) 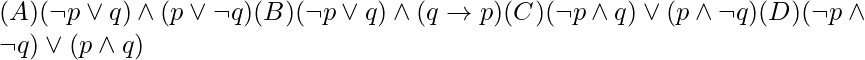
Para obtener una solución, consulte GATE | GATE-CS-2015 (Conjunto 1) | Pregunta 65
Referencias- Lógica proposicional – Wikipedia Principio de explosión – Wikipedia
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen
Leer la siguiente parte: Introducción a la Lógica Proposicional – Conjunto 2
Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA