Una array representa una colección de números dispuestos en un orden de filas y columnas. Es necesario encerrar los elementos de una array entre paréntesis o corchetes.
A continuación se muestra una array con 9 elementos.
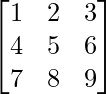
Esta Array [M] tiene 3 filas y 3 columnas. Se puede hacer referencia a cada elemento de la array [M] por su número de fila y columna. Por ejemplo, un 23 = 6
Orden de una array:
el orden de una array se define en términos de su número de filas y columnas.
Orden de una array = No. de filas × No. de columnas
Por lo tanto Matrix [M] es una array de orden 3 × 3.
Transpuesta de una array:
La transpuesta [M] T de una array mxn [M] es la array nxm obtenida al intercambiar las filas y columnas de [M].
si A= [a ij ] mxn , entonces A T = [b ij ] nxm donde b ij = a ji
Propiedades de transpuesta de una array:
- (UN T ) T = UN
- (A+B) T = UN T + B T
- (AB) T = B T UN T
Array singular y no singular:
- Array singular: se dice que una array cuadrada es array singular si su determinante es cero, es decir, |A|=0
- Array no singular: Se dice que una array cuadrada es array no singular si su determinante es distinto de cero.
Propiedades de la suma y multiplicación de arrays:
- A+B = B+A (Conmutativo)
- (A+B)+C = A+ (B+C) (Asociativo)
- ¿AB? BA (no conmutativo)
- (AB) C = A (BC) (Asociativo)
- A (B+C) = AB+AC (Distributivo)
Array cuadrada: una array cuadrada tiene tantas filas como columnas. es decir, número de filas = número de columnas.
Array simétrica: se dice que una array cuadrada es simétrica si la transpuesta de la array original es igual a su array original. es decir, (A T ) = A.
Sesgada simétrica: Una array sesgada simétrica (o antisimétrica o antimétrica[1]) es una array cuadrada cuya transpuesta es igual a su negativo. Es decir, (A T ) = -A.
Array diagonal: una array diagonal es una array cuadrada en la que las entradas fuera de la diagonal principal son todas cero. El término generalmente se refiere a arrays diagonales cuadradas.
Array Identidad: Una array cuadrada en la que todos los elementos de la diagonal principal son unos y todos los demás elementos son ceros. La array identidad se denota como I.
Array ortogonal: Se dice que una array es ortogonal si AA T = A T A = I
Array idempotente: Se dice que una array es idempotente si A 2 = A
Array involuntaria: Se dice que una array es Involutario si A 2 = I.
Nota: cada array cuadrada se puede expresar de forma única como la suma de una array simétrica y una array asimétrica. A = 1/2 (A T + A) + 1/2 (A – A T ).
Adjunto de una array cuadrada: El adjunto de una array A es la transpuesta de la array cofactor de A
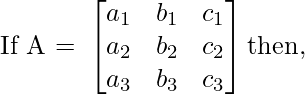
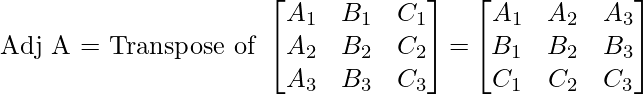
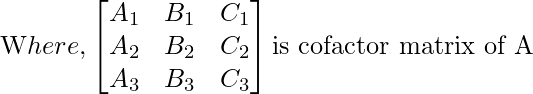
Propiedades del Adjunto:
- A(Adj A) = (Adj A) A = |A| yo norte
- Adj(AB) = (Adj B).(Adj A)
- |Adj A|= |A| n-1
- Adj(kA) = k n-1 Adj(A)
- |adj(adj(A))|= |A|^(n-1)^2
- adj(adj(A))=|A|^(n-2) * A
- Si A = [L,M,N] entonces adj(A) = [MN, LN, LM]
- adj(yo) = yo
Donde, “n = número de filas = número de columnas”
Inversa de una array cuadrada:
![]()
Aquí |A| no debe ser igual a cero, significa que la array A no debe ser singular.
Propiedades de la inversa:
1. (A -1 ) -1 = A
2. (AB) -1 = B -1 A -1
3. Sólo una array cuadrada no singular puede tener inversa.
¿Dónde debemos usar la array inversa?
Si tienes un conjunto de ecuaciones simultáneas:
7x + 2y + z = 21
3y – z = 5
-3x + 4y – 2x = -1
Como sabemos cuando AX = B, entonces X = A -1 B, entonces calculamos el inverso de A y al multiplicarlo B, podemos obtener los valores de x, y y z.
Rastro de una array: el rastro de una array se denota como tr(A), que se usa solo para una array cuadrada y es igual a la suma de los elementos diagonales de la array. Recuerde que la traza de una array también es igual a la suma del valor propio de la array. Por ejemplo:
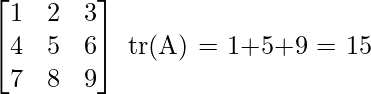
Este artículo es una contribución de Nitika Bansal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA