Matemáticas | La probabilidad condicional

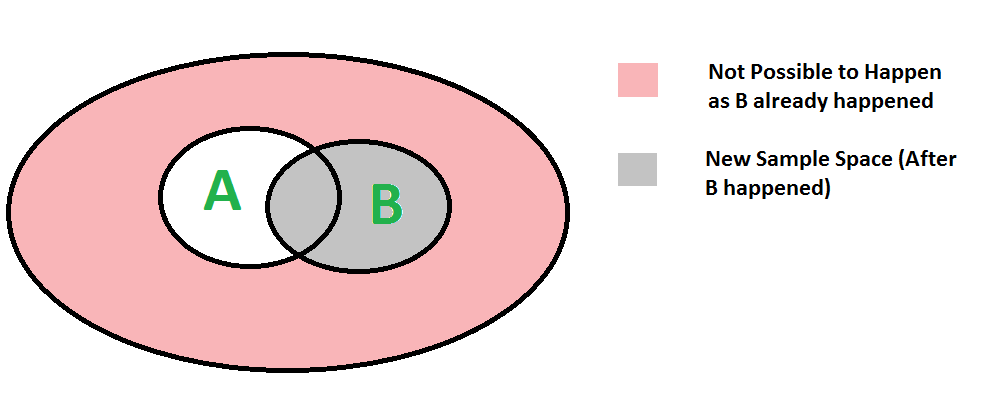
La probabilidad condicional P(A | B) indica la probabilidad de que suceda el evento ‘A’ dado que sucedió el evento B.

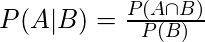
Podemos entender fácilmente la fórmula anterior usando el siguiente diagrama. Como B ya sucedió, el espacio muestral se reduce a B. Entonces, la probabilidad de que A suceda se divide por P(B)

Ejemplo:
en un lote, hay un 80 % de programadores de C y un 40 % son programadores de Java y C. ¿Cuál es la probabilidad de que un programador de C también sea programador de Java?

Let A --> Event that a student is Java programmer
    B --> Event that a student is C programmer
    P(A|B) = P(A ∩ B) / P(B)
           = (0.4) / (0.8)
           = 0.5
So there are 50% chances that student that knows C also 
knows Java 

Regla del producto:
derivada de la definición anterior de probabilidad condicional al multiplicar ambos lados por P(B)

   P(A ∩ B) = P(B) * P(A|B) 

Comprender la probabilidad condicional a través del árbol: el
cálculo de la probabilidad condicional se puede realizar utilizando el árbol. Este método es muy útil y rápido cuando se trata de muchos problemas.

Ejemplo: en cierta biblioteca, el veinte por ciento de los libros de ficción están desgastados y necesitan reemplazo. El diez por ciento de los libros de no ficción están desgastados y necesitan reemplazo. El cuarenta por ciento de los libros de la biblioteca son de ficción y el sesenta por ciento son de no ficción. ¿Cuál es la probabilidad de que un libro elegido al azar esté usado? Dibuja un diagrama de árbol que represente los datos.

Solución: Sea F un libro de ficción y N un libro de no ficción. Deje que W represente libros usados ​​y G representa libros no usados.

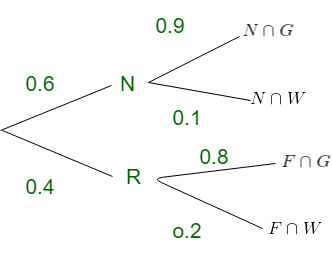
P(worn)= P(N)*P(W | N) + P(F)*P(W | F)
              
           = 0.6*0.1  +  0.4* 0.2      
           = 0.14

Ejercicio:
1) ¿Cuál es el valor de P(A|A)?

2) Sea P(E) la probabilidad del evento E. Dado P(A) = 1, P(B) = 1/2, los valores de P(A | B) y P(B | A) respectivamente son (GATE CS 2003)
(A) 1/4, 1/2
(B) 1/2, 1/14
(C) 1/2, 1
(D) 1, 1/2
Vea esto para la solución.

Referencias:
http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-042j-mathematics-for-computer-science-fall-2010/video-lectures/lecture-19-conditional- probabilidad/

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.