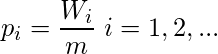El modelo de distribución hipergeométrica se utiliza para estimar el número de fallas inicialmente residentes en un programa al comienzo del proceso de prueba o depuración en función de la distribución hipergeométrica. Sea ![]() el número acumulado de errores ya detectados hasta ahora por
el número acumulado de errores ya detectados hasta ahora por ![]() , y
, y ![]() sea el número de errores detectados recientemente por tiempo
sea el número de errores detectados recientemente por tiempo ![]() .
.
Suposiciones:
- Un programa inicialmente contiene m fallas cuando comienza la fase de prueba.
- Una prueba se define como un número de instancias de prueba que son pares de datos de entrada y datos de salida. En otras palabras, la colección de operaciones de prueba realizadas en un día o una semana se denomina instancia de prueba. Las instancias de prueba se denotan por
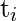 i = 1, 2, . . ., n.
i = 1, 2, . . ., n. - Las fallas detectadas no se eliminan entre instancias de prueba.
Por lo tanto, a partir de la última suposición, se pueden experimentar las mismas fallas en varias instancias de prueba. Sea ![]() el número de fallas experimentadas por instancia de prueba
el número de fallas experimentadas por instancia de prueba ![]() . Cabe señalar que algunas de las
. Cabe señalar que algunas de las ![]() fallas pueden ser las que ya se cuentan en
fallas pueden ser las que ya se cuentan en ![]() , y las fallas Wi restantes representan las fallas recién detectadas.
, y las fallas Wi restantes representan las fallas recién detectadas.
Si ![]() es una instancia observada de
es una instancia observada de ![]() , entonces podemos ver eso
, entonces podemos ver eso ![]() . Cada falla se puede clasificar en una de dos categorías:
. Cada falla se puede clasificar en una de dos categorías:
- Fallas recién descubiertas
- fallas redescubiertas
Si asumimos que el número de fallas recién detectadas ![]() sigue una distribución hipergeométrica, entonces la probabilidad de obtener exactamente
sigue una distribución hipergeométrica, entonces la probabilidad de obtener exactamente ![]() fallas recién detectadas entre las
fallas recién detectadas entre las ![]() fallas es,
fallas es,
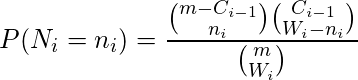
dónde
![]()
y
![]()
para todo yo Dado ![]() que se supone que se distribuye hipergeométricamente, el número esperado de fallas recién detectadas durante el intervalo
que se supone que se distribuye hipergeométricamente, el número esperado de fallas recién detectadas durante el intervalo ![]() es,
es,
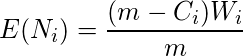
y el valor esperado de ![]() está dado por,
está dado por,
![Rendered by QuickLaTeX.com $$E(C_i)=m\left [1- \prod_{j=1}^i (1-p_i) \right ]$$](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-114fe799934bac78c7c7eb945a095280_l3.png)
dónde